tanの微分

$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}\def\opdf{\opcol{\mathrm df}}\def\coldf{\tcol{\mathrm df}}$

「微分する」という言葉

最初に、「微分する」という言葉が２種類に使われているということについて注意しておいた。

1. $\ycol{y}=f\kakko{\xcol{x}}$の導関数を求める（結果：${\ycol{\mathrm dy}\over\xcol{\mathrm dx}}=f'\kakko{\xcol{x}}$）
2. $\ycol{y}=f\kakko{\xcol{x}}$の（両辺の）微小変化を求める（結果：$\ycol{\mathrm dy}=f'\kakko{\xcol{x}}\ycol{\mathrm dx}$）

前者は「$x$で微分する」のように変数を指定することも多い。

---

　前回の復習として$\ycol{y}=\sin\thetacol{\theta}$の微分を図解および数式では確認した後、$\ycol{y}=\tan\thetacol{\theta}$の微分をまず図で考えた。

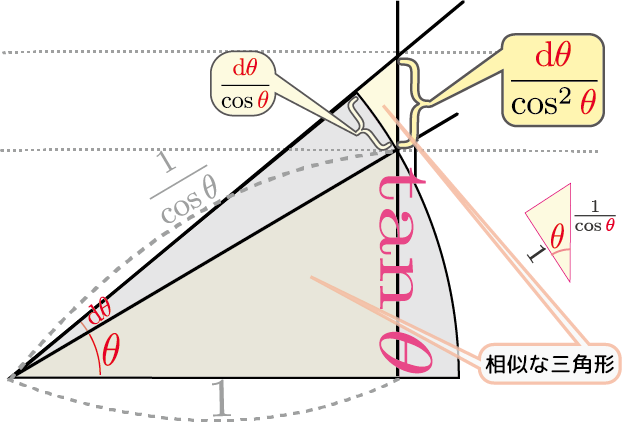
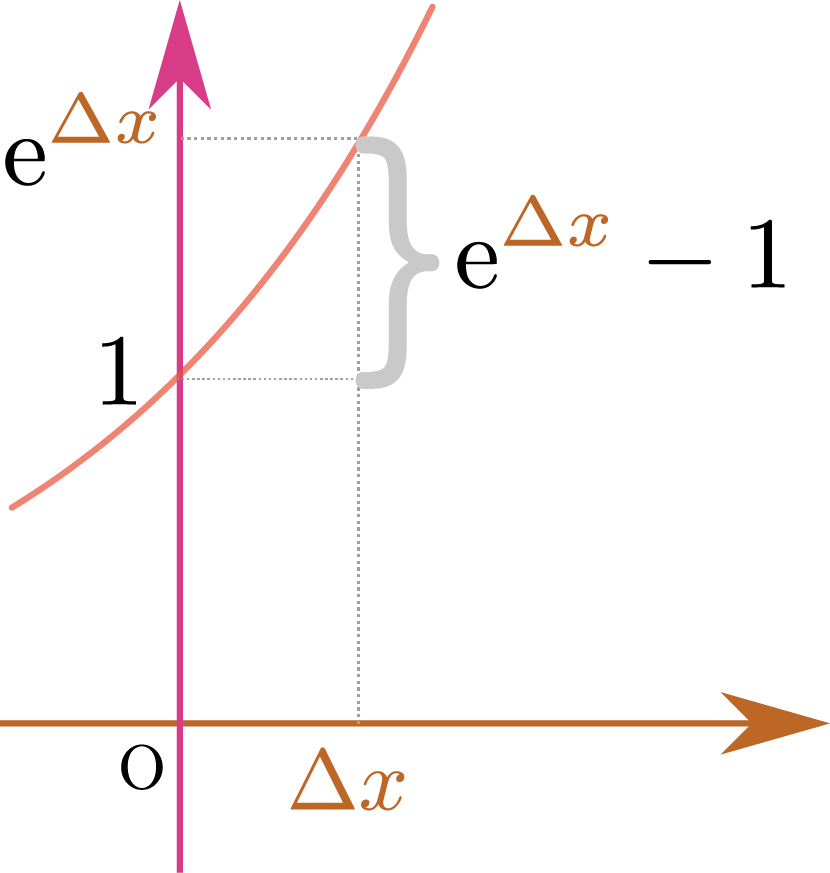
　上の図のように、底辺1の直角三角形を描く（この三角形の高さは$\tan\thetacol{\theta}$である）。角度が$\coldtheta$だけ大きくなった時、この直角三角形の高さがどれだけ高くなるかを考えれば$\tan \thetacol{\theta}$の微分がわかる。

　この直角三角形の斜辺の長さは${1\over \cos\thetacol{\theta}}$であるこれを求めるのに、「公式$1+\tan^2\thetacol{\theta}={1\over \cos^2\thetacol{\theta}}$を使って…」などとやり始める人がたまにいるのだが、そんな面倒なことは全く必要ない。${底辺\over 斜辺}=\cos \thetacol{\theta}$という式を思い出せばすぐに出る。から、図に書いた円弧の部分の長さは${\coldtheta\over \cos\thetacol{\theta}}$である。また相似な三角形ができているから、その相似の関係を使えば、高さの増加は${\coldtheta\over \cos^2\thetacol{\theta}}$とわかり、$\ddtheta\tan\thetacol{\theta}={1\over \cos^2\thetacol{\theta}}$が導かれる。

　次に数式を使って微分しよう。$\tan \thetacol{\theta}={{\sin \thetacol{\theta}\over \cos\thetacol{\theta}}}$を使う。ここで分数関数の微分の式に代入して考えるという方法もある。が、ここでは分母を払って、$\cos\thetacol{\theta}\times\ycol{y}=\sin\thetacol{\theta}$としてから微分する（この「微分する」は上の2.の意味）。 \begin{equation} \begin{array}{crll} \goverbrace{ -\sin\thetacol{\theta} \coldtheta}^{\cos\thetacol{\theta}の微分}\times\ycol{y} +&\cos\thetacol{\theta}\times \coldy =&\cos \thetacol{\theta} \coldtheta &\kokode{\cos \thetacol{\theta}で割る} \\[-2mm] - \underbrace{\sin\thetacol{\theta} \over \cos\thetacol{\theta}}_{\tan\thetacol{\theta}} \coldtheta\times\goverbrace{\tan\thetacol{\theta}}^{\ycol{y} }& +\coldy =&\coldtheta &\kokode{左辺第1項移項} \\[-2mm] &\coldy =&\underbrace{(1+\tan^2 \thetacol{\theta})}_{{1\over \cos^2\thetacol{\theta}}}\coldtheta \end{array} \end{equation} のように微分を行うと、以下の式を得る。

---

$\tan$の微分

\begin{equation} \begin{array}{rl} \diff (\tan\thetacol{\theta})={1\over \cos^2\thetacol{\theta}}\coldtheta,~~~~~ \ddtheta (\tan\thetacol{\theta})={1\over \cos^2\thetacol{\theta}} \end{array} \end{equation}

---

　この計算は各自ノートでやってもらったが、さっとできる人とできない人の差が大きかった。できなかった、という人は教科書に載っている問題などを自力でやってみておくこと。

　教科書には${\rm cosec},\sec,\cot$の微分も載っているが、そこは自習。

$\arcsin$の微分

　$\sin$の逆関数だから、逆関数の微分を使ってもよいし、たとえば$\ycol{y}=\arcsin\xcol{x}$を微分するなら、まず$\xcol{x}=\sin{\ycol{y}}$とした後、 \begin{equation} \begin{array}{rll} \xcol{x}=&\sin\ycol{y}&\kokode{微分} \\[-3mm] \coldx=&\cos\ycol{y}\coldy&\kokode{整理して}\\[-3mm] {\coldy\over \coldx}=&{1\over \cos\ycol{y}}=\pm{1\over \sqrt{1-\xcol{x}^2}}\\ \end{array} \end{equation} のように微分を行ってもよい。複号$\pm$が問題となるが、

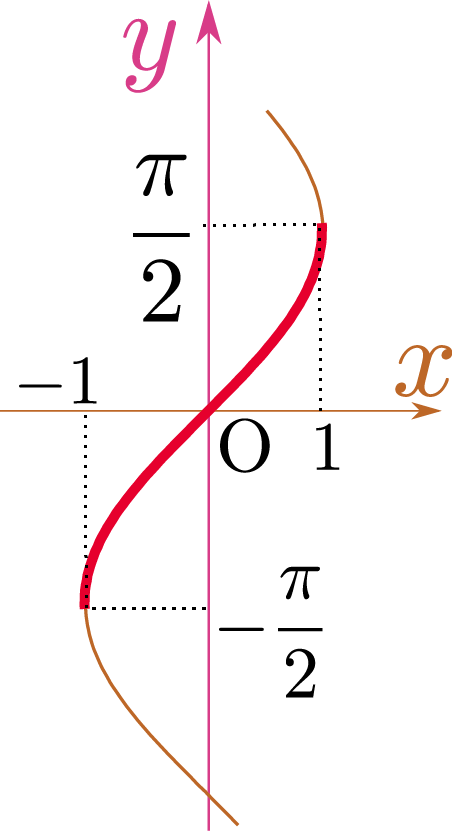
のグラフのように$\arcsin$を定義した場合、$\arcsin$はこの定義域・値域の中では常に増加するから、$\ddx\arcsin\xcol{x}={1\over \sqrt{1-\xcol{x}^2}}$でよい値域を変えると、増加する関数とは限らないから、その場合は符号を調整する必要がある。。

　教科書には$\arccos,\arctan$の微分も載っているが、そこは自習。

指数関数・対数関数の微分

指数関数の微分

　指数関数$\ycol{y}=\E^{\xcol{x}}$の微分を、「微分の定義」まで戻って考えると、 \begin{equation} {\ddx}\left(\E^\xcol{x}\right)= \lim_{\xcol{\Delta x}\to0}{\E^{\xcol{x}+\xcol{\Delta x}}-\E^\xcol{x}\over \xcol{\Delta x}} =\E^\xcol{x} \times\lim_{\xcol{\Delta x}\to0}{\E^{\xcol{\Delta x}}-1\over \xcol{\Delta x}} \end{equation} のように、極限の式から$\E^{\xcol{x}}$が外に出てしまう。こんなふうに外に出せてしまうのは、指数関数という関数が「$\xcol{x}$が$\xcol{\Delta x}$増加すると「元の値」の$\E^{\xcol{\Delta x}}$倍になる」という性質を持っている（ということは増加量も元の関数の値に比例する）おかげである。

　残った部分$\lim_{\xcol{\Delta x}\to0}{\E^{\xcol{\Delta x}}-1\over \xcol{\Delta x}}$はよく見ると$\xcol{x}$によらない定数である。これは$\ycol{y}=\E^\xcol{x}$の$\xcol{x}=0$での傾きそのもの（次のグラフ参照）

であり、その値は$\E$の定義により1である。よって、

---

指数関数の微分

\begin{equation} {\ddx}\left( \E^{\xcol{x}}\right)=\E^\xcol{x}\label{expbibun} \end{equation}

---

である。$\E^{\xcol{x}}$という関数は\fukidasi{微分しても変わらない関数}だとわかる（だから$\E$は重要なのだ）。

「微分しても変わらない関数ってどんなもの？」という視点から、指数関数を「導いて」みよう。

　我々は$\E^{\xcol{x}}$の$\xcol{x}=0$での値が1で傾きが1であること、つまり$\xcol{x}$が小さいとき、$\E^\xcol{x}\simeq 1+\xcol{x}$を知っている。しかし、$1+\xcol{x}$を微分すると \begin{equation} \ddx \left(1+\xcol{x}\right)\stackrel{?}{=}1 \end{equation} となって元に戻らない。右辺に$\xcol{x}$がいるためには、左辺の括弧内（微分される関数）に${1\over 2}\xcol{x}^2$を加えておくとよいだろう。しかし、 \begin{equation} \ddx \left(1+\xcol{x}+{1\over 2}\xcol{x}^2\right)\stackrel{?}{=}1+\xcol{x} \end{equation} であるから、今度は（右辺に${1\over 2}\xcol{x}^2$が足りず）元に戻らない。そこでさらに${1\over 2\times3}\xcol{x}^3$を加える。すると、 \begin{equation} \ddx \left(1+\xcol{x}+{1\over 2}\xcol{x}^2+{1\over 2\times3}\xcol{x}^3\right)\stackrel{?}{=}1+\xcol{x}+{1\over 2}\xcol{x}^2 \end{equation} となる。この手順を繰り返していくと考えれば、指数関数は \begin{equation} \begin{array}{rl} \E^{\xcol{x}}=&1+\xcol{x}+{1\over 2}\xcol{x}^2+{1\over \underbrace{2\times3}_{3!}}\xcol{x}^3 +{1\over \underbrace{2\times 3\times 4}_{4!}}\xcol{x}^4+{1\over \underbrace{2\times 3\times 4\times 5}_{5!}}\xcol{x}^5 +\cdots \end{array} \end{equation} という無限につづく項の和で書けることがわかる。

　前に$1+1+{1\over 2}+{1\over 2\times3}+{1\over 2\times 3\times 4}+{1\over 2\times 3\times 4\times 5}+\cdots$という計算で$\E$が出せる、という話をしたが、その理由はこれである。後で、「テイラー展開」という方法を使って同じ式が出てくることを見る。

　次に$\E^{k\xcol{x}}$のように指数が定数倍（$k$倍）されている場合を考えると、$\tcol{t}=k\xcol{x}$と置けば、 \begin{equation} {\ddx (\E^{k\xcol{x}})}=\underbrace{{\coldt\over \coldx}}_k\underbrace{\ddt \E^{\tcol{t}}}_{\E^{\tcol{t}}}= k\E^{k\xcol{x}} \end{equation} となるこのような状況（微分したことにより、$\E^{k\xcol{x}}$が$k$倍される）を「$k$が$\exp$の肩から降りてくる」と表現する。。底が$\E$ではない場合も$a=\E^{\log a}$ゆえに$a^{\xcol{x}}=\E^{\log a \times \xcol{x}}$と書けることを使って

---

一般の指数関数の微分

\begin{equation} \ddx (a^\xcol{x})= a^\xcol{x} \log a \end{equation}

---

がわかる（$a=\E$なら、$\log\E=1$だから元の式に戻る）。

また、合成関数の微分を使えば、以下の式もわかる。

---

関数を指数とする関数の微分

\begin{equation} \ddx \left(\E^{f\kakko{\xcol{x}}}\right)= f'\kakko{\xcol{x}}\E^{f\kakko{\xcol{x}}} \end{equation}

---

対数関数の微分

$\ycol{y}=\log\xcol{x}$を微分するには、まず$\E^\ycol{y}=\xcol{x}$として、両辺を微分し、 \begin{equation} \begin{array}{rl} \underbrace{\E^\ycol{y}}_{\xcol{x}}\coldy =&\coldx \\ {\coldy \over \coldx}=& {1\over \xcol{x}} \end{array} \end{equation} とすればよい（もちろん、$\E^{\ycol{y}}$の逆関数を微分しているから、$\E^{\ycol{y}}$の微分（やはり$\E^{\ycol{y}}$）の逆数である${1\over \E^{\ycol{y}}}$になると考えてもよい)。

---

対数関数の微分

\begin{equation} \ddx (\log\xcol{x})={1\over \xcol{x}}~~~（これは底が\E の時に限る）\label{difflog} \end{equation}

---

前に、$\xcol{x}^\alpha$のような冪の形で、微分して${1\over \xcol{x}}$になる多項式はないという話をしたが、多項式で書けない$\ycol{y}=\log\xcol{x}$がまさにその関数となる。

　指数関数・対数関数の近似式としては、 \begin{eqnarray} \E^{\xcol{x}}&=&1+\xcol{x}+\Odr\kakko{\xcol{x}^2}\\ \log\kakko{1+\xcol{x}}&=& \xcol{x}+\Odr\kakko{\xcol{x}^2}\label{logkinji} \end{eqnarray} という式がよく使われる（この二つの式は互いに逆関数になるという関係でつながっている）。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。