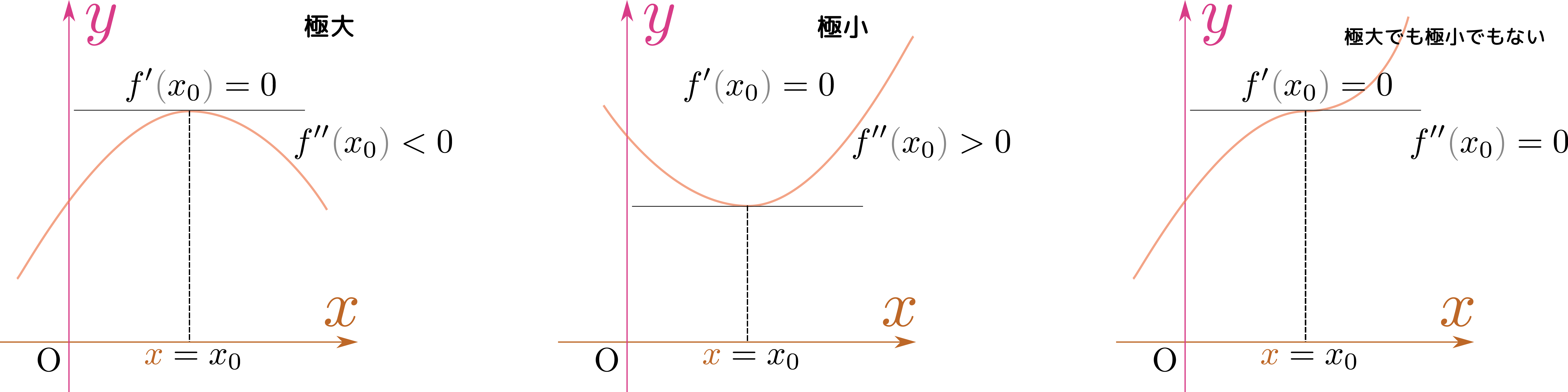高階微分

$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}\def\opdf{\opcol{\mathrm df}}\def\coldf{\tcol{\mathrm df}}\def\dtwof{\opcol{\mathrm d^2f}}$

高階微分

　導関数$f'\kakko{\xcol{x}}=\lim_{\xcol{\Delta x}\to0}{f\kakko{\xcol{x}+\xcol{\Delta x}}-f\kakko{\xcol{x}}\over \xcol{\Delta x}}$の導関数 \begin{equation} f''\kakko{\xcol{x}}=\lim_{\xcol{\Delta x}\to0}{f'(\xcol{x}+\xcol{\Delta x})-f'\kakko{\xcol{x}}\over \xcol{\Delta x}} \end{equation} を作ってみよう。これを「二階微分」または「二階導関数」この意味で「二回微分」「二回導関数」と書く人がいるが、これは誤字である（しかし発音では区別がつかないから安心だ）。と呼び、記号としては$'$を重ねて$f''\kakko{\xcol{x}}$と表現することにしよう（$f\kakko{\xcol{x}}\to f'\kakko{\xcol{x}}$が「一階微分」、$f\kakko{\xcol{x}}\to f'\kakko{\xcol{x}}\to f''\kakko{\xcol{x}}$が「二階微分」である）。また、一階微分を$\ddx f\kakko{\xcol{x}}$と書いたように、二階微分は以下のように表現してもよい。 \begin{equation} f''\kakko{\xcol{x}}= \ddx \left( \ddx f\kakko{\xcol{x}} \right)= \left(\ddx\right)^2 f\kakko{\xcol{x}}= \opcol{\diff ^2\over \kidx^2} f\kakko{\xcol{x}}={\dtwof\over \kidx^2}\kakko{\xcol{x}}\label{nikai} \end{equation}

　同様に三階微分や四階微分も定義される。$n$階微分は$f^{(n)}\kakko{\xcol{x}}$とも表現する。

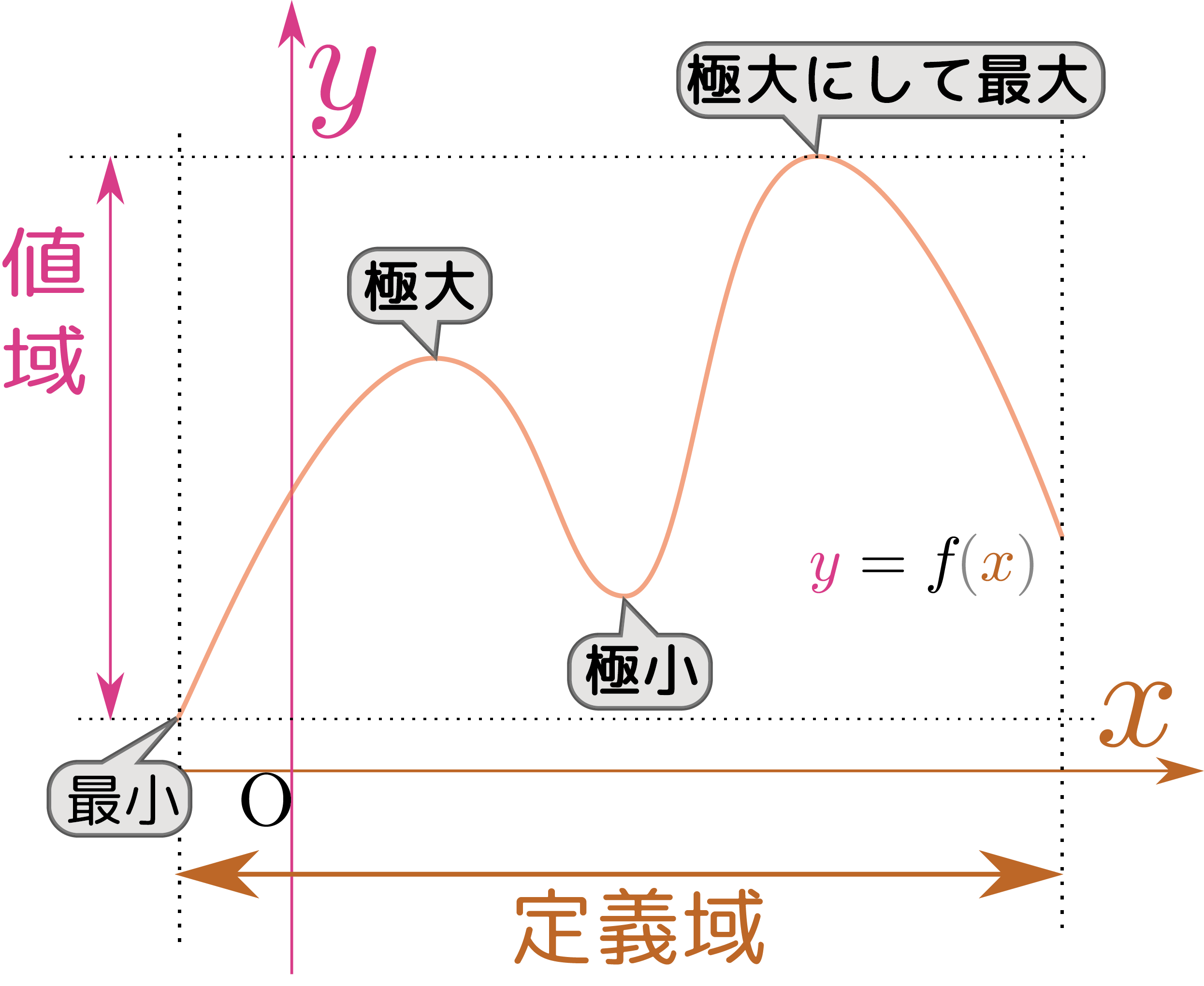
　二階微分がどんな意味を持つかを考えよう。二次関数や三次関数の形を考えたときに、1次の項の係数（$\xcol{x}$の前の係数）が$\xcol{x}=0$における傾きを、2次の項の係数（$\xcol{x}^2$の前の係数）が$\xcol{x}=0$における「曲がり具合」を表現していたのを覚えているだろうか。たとえば結果$6a\xcol{x}+2b$を見ると、$\xcol{x}=0$における二階微分の値$2b$が「$\xcol{x}^2$の係数の2倍」であるから、この数は「曲線の曲がり具合」を表現する。これは三次関数に限らずどんな関数に対しても言える。

　定義式から計算することで二階微分が「曲がり具合」を表すことを確認しよう。

　まず、$ f''\kakko{\xcol{x}}=\lim_{\xcol{\Delta x}\to0}{f'\kakko{\xcol{x}+\xcol{\Delta x}}-f'\kakko{\xcol{x}}\over \xcol{\Delta x}}$という二階微分の意味を表した式そのものに、一階微分の式$\lim_{\xcol{\delta x}\to0}{f\kakko{\xcol{x}+\xcol{\delta x}}-f\kakko{\xcol{x}}\over \xcol{\delta x}}$を代入する。ここで、（すぐ後で同じにするのだが）二つの極限は別のものなので、一階微分の方はいつもの$\xcol{\Delta x}$ではなく$\xcol{\delta x}$という記号を用いておく。すると、 \begin{equation} \begin{array}{rll} f''\kakko{\xcol{x}} =&\lim_{\xcol{\Delta x}\to0}{\overbrace{ \lim_{\xcol{\delta x}\to0}{f\kakko{\xcol{x}+\xcol{\Delta x}+\xcol{\delta x}}-f\kakko{\xcol{x}+\xcol{\Delta x}}\over \xcol{\delta x}}}^{f'\kakko{\xcol{x}+\xcol{\Delta x}}} -\overbrace{\lim_{\xcol{\delta x}\to0}{f\kakko{\xcol{x}+\xcol{\delta x}}-f\kakko{\xcol{x}}\over \xcol{\delta x}}}^{f'\kakko{\xcol{x}}} \over \xcol{\Delta x} } \\[3mm] =&\lim_{\xcol{\Delta x}\to0}\lim_{\xcol{\delta x}\to0} {\left( f\kakko{\xcol{x}+\xcol{\Delta x}+\xcol{\delta x}}-f\kakko{\xcol{x}+\xcol{\Delta x}}\right) -\left( f\kakko{\xcol{x}+\xcol{\delta x}}-f\kakko{\xcol{x}}\right) \over \xcol{\Delta x}\xcol{\delta x} } \end{array} \end{equation} という式が出る。この後、二つの極限$\xcol{\Delta x}\to0$と$\xcol{\delta x}\to0$を行わなくてはいけない元々の式からするとまず$\xcol{\delta x}\to0$の極限を取ってから次に$\xcol{\Delta x}\to0$の極限を取るべきなのだが、結果を見ると$\xcol{\Delta x}\leftrightarrow\xcol{\delta x}$という交換で対称な式になっているので、実は極限の順番は変えても問題ない。。

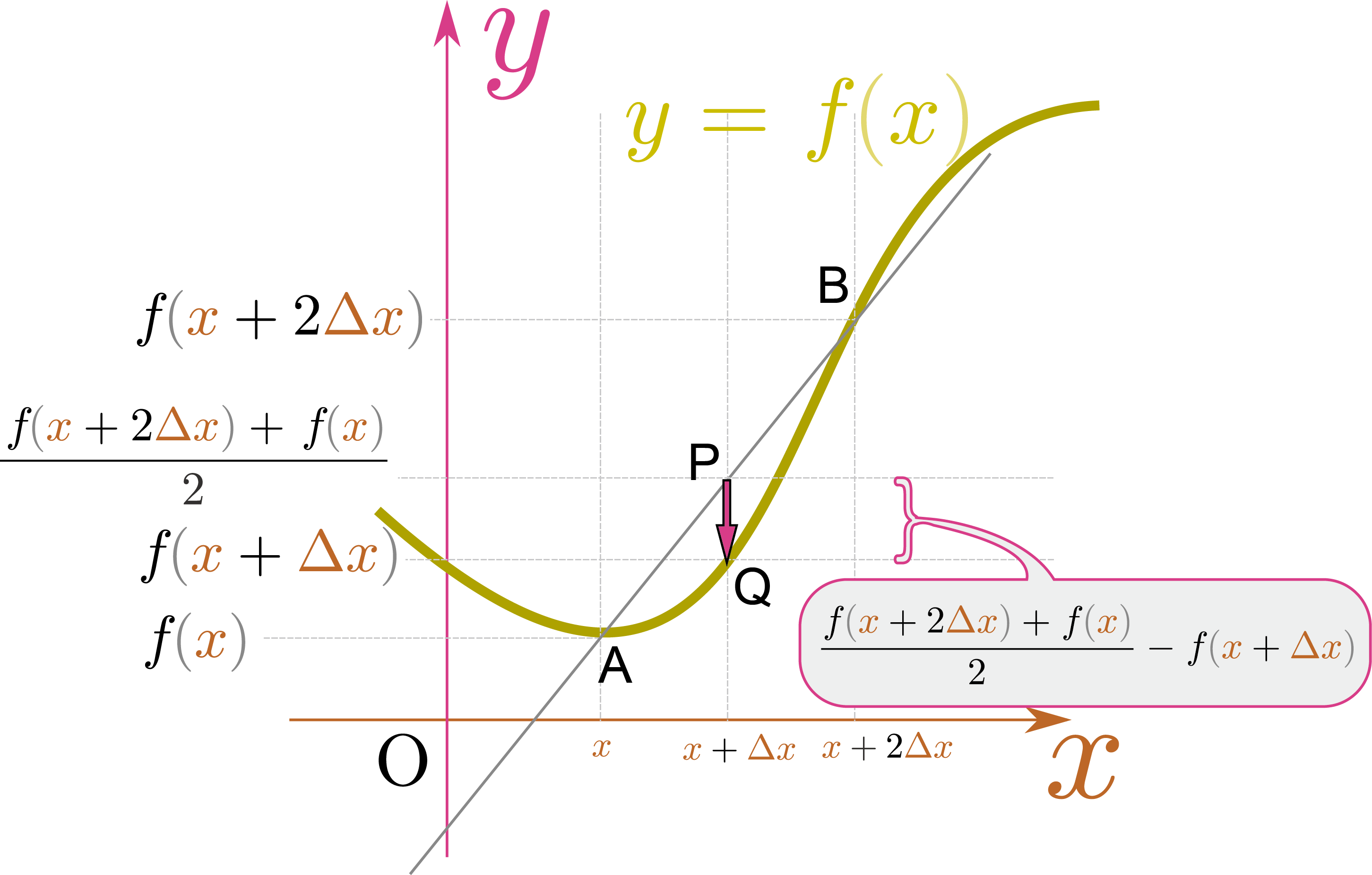
　ここではこの式の分子の意味を知ることが目的なので厳密に考えることなく、$\xcol{\delta x}=\xcol{\Delta x}$と置いて極限の記号を一つにして書き直すと、 \begin{equation} \begin{array}{rll} f''\kakko{\xcol{x}} =&\lim_{\xcol{\Delta x}\to0}{\left( f\kakko{\xcol{x}+2\xcol{\Delta x}}-f\kakko{\xcol{x}+\xcol{\Delta x}}\right) -\left( f\kakko{\xcol{x}+\xcol{\Delta x}}-f\kakko{\xcol{x}}\right) \over (\xcol{\Delta x})^2 } \\ =&\lim_{\xcol{\Delta x}\to0}{ f\kakko{\xcol{x}+2\xcol{\Delta x}}-2f\kakko{\xcol{x}+\xcol{\Delta x}} +f\kakko{\xcol{x}} \over (\xcol{\Delta x})^2 }\\ =&2\lim_{\xcol{\Delta x}\to0}{ { f\kakko{\xcol{x}+2\xcol{\Delta x}} +f\kakko{\xcol{x}}\over 2} -f\kakko{\xcol{x}+\xcol{\Delta x}} \over (\xcol{\Delta x})^2 } \end{array}\label{nikaibibunteigi} \end{equation} という計算になる。最後で2を前に出したのは、分子の \begin{equation} {f\kakko{\xcol{x}+2\xcol{\Delta x}}+f\kakko{\xcol{x}}\over 2}-f\kakko{\xcol{x}+\xcol{\Delta x}}\label{heikinsa} \end{equation} に図形的意味があるからである。その意味を知るため、右のグラフを見て欲しい。図の点Pは点A$(\xcol{x},f\kakko{\xcol{x}})$と点B$(\xcol{x}+2\xcol{\Delta x},f\kakko{\xcol{x}+2\xcol{\Delta x}})$の中点である。

　P点の高さは${f\kakko{\xcol{x}+2\xcol{\Delta x}}+f\kakko{\xcol{x}}\over 2}$、すなわち点Aの高さと点Bの高さの平均値である。一方$f\kakko{\xcol{x}+\xcol{\Delta x}}$は点Qの高さである。こう考えると、この量は「線分ABの中点に比べて点Qがどれだけ下がっているか」を示す量であり、「線の曲がり具合」を表現している。二階微分の値は「両隣の平均に比べて自分がどれだけ下がっているか」を示す量なのだ。

　自然において、二階微分が正なら増加し、二階微分が負なら減るという傾向、グラフで表現すれば下に凸なら増加、凸なら減少という傾向を持つ現象はたくさんある。これはすなわち平坦に戻そうという現象だ（たとえば水面・温度分布・濃度分布などにこういう傾向がある）。

　最後に書いた${\dtwof \over \kidx^2}\kakko{\xcol{x}}$という表現を見て、（${\coldy\over \coldx}$を「$\xcol{x}$の微小変化と$\ycol{y}$の微小変化の比」と解釈をしたのを思い出して）「${\dtwof \over \kidx^2}$の分子の$\dtwof$ってなんなんだ？」と不思議に思うかもしれない。

　照らしあわせて考えると、 $\dtwof$は$f\kakko{\xcol{x}+2\xcol{\Delta x}}-2f\kakko{\xcol{x}+\xcol{\Delta x}} +f\kakko{\xcol{x}}$（つまり両端の和引く中間の2倍）という式の$\xcol{\Delta x}\to0$の極限（これは$\Odr\kakko{\xcol{\Delta x}^2}$の微小量）に対応する、ということになる。

　$n$次の多項式は、$n$階微分すると定数となり、$(n+1)$階微分すると0になる。$n$次の冪の微分は、$\xcol{x}^n\to n\xcol{x}^{n-1}\to n(n-1)\xcol{x}^{n-2}\to\cdots\to n!\xcol{x} \to n!\to0$という流れになり、0が終着点となる。一方、$\xcol{x}^\alpha$（$\alpha$は正の整数でない）や三角関数、指数関数、対数関数などは何度微分しても0にはならない。たとえば$\log\xcol{x}$から始めると、$\log\xcol{x}\to{1\over \xcol{x}}\to-{1\over\xcol{x}^2}\to{2\over\xcol{x}^3}\to\cdots{(-1)^nn!\over \xcol{x}^{n+1}}\to\cdots$となり、無限に続く。

　指数関数の場合、$\E^{\xcol{x}}$は何度$\xcol{x}$で微分しても$\E^{\xcol{x}}$のままである。$\E^{k\xcol{x}}$の場合、 \begin{equation} \E^{k\xcol{x}} \to k \E^{k\xcol{x}} \to k^2 \E^{k\xcol{x}} \to k^3 \E^{k\xcol{x}} \to k^4 \E^{k\xcol{x}}\to\cdots \end{equation} のように微分すると前に定数$k$がどんどん落ちてくる（$n$階微分すると$k^n$が前につく）。このことを「$k$が$\exp$の肩から降りてくる」と表現する。

　三角関数の一つである$\sin$は \begin{equation} \sin\xcol{x}\to \cos\xcol{x} \to -\sin\xcol{x} \to -\cos\xcol{x} \to \sin\xcol{x} \to \cdots \end{equation} のように符号が変わりつつ$\sin\leftrightarrow \cos$を移り変わる（二階微分すると元の関数の$-1$倍になるこれが指数関数と三角関数が「自乗すると$-1$になる数＝虚数$\I$」を通じて関係してくる式であるオイラーの関係式~~$\E^{\scriptI\thetacol{\theta}}=\cos\thetacol{\theta}+\I\sin\thetacol{\theta}$の成立に深く関係している。）。

微分と極大・極小

極大・極小

　微分のもう一つの重要な使い途は「極大・極小がどこか求める」ことにある。「極大(maximal)」と「極小(minimal)」は「最大・最小」に似ているが、違いは「最大・最小」は関数の定義域全体において最も大きい（あるいは小さい）値を取る場合を意味するが、「極大・極小」は定義域全体ではなく、考えている「点」の近傍「ある点の近傍」とは、その点を内部に含むような領域のこと。「近傍」の範囲は狭くてもよいが、必ず両側を含む。においてのみ最も大きい（あるいは小さい）値をとっていればよい「極大」「極小」はつまり「局所的最大」「局所的最小」である。英語でそれぞれ「local maximum」「local minimum」と呼ぶこともある。「maximum(minimum)」は「最大（最小）」。「-mum」と「-mal」の違いに注意。。

　図に簡単な例で極大・極小となっている点と、考えている定義域内で最大・最小である点を示した図で「最小」とのみマークした点（定義域の下限になっている）はその点が考えている領域の端点であって領域の内部にはないから、最小にはなっているが「極小」ではない。。極大または極小である状況でかつ関数がその点で微分可能であるならば、その点では一階微分$f'\kakko{\xcol{x}}$が0になっていなくてはいけない微分不可能な、「尖った」点が極大・極小になっていることもあり得る。。

　連続で、しかも少なくとも二階微分可能であるような関数を考える。この関数$f\kakko{\xcol{x}}$がある点$\xcol{x}=x_0$において一階微分が0になった（$f'\kakko{\xcol{x}}=0$）とする。もしこの点で二階微分が負（次の図の左側）ならば、この場合この点では極大である。逆に正（次の図の中央）ならば、この点では極小である。

　二階微分が0である場合二階微分が0であり、かつその点の前後で二階微分が符号を変える場合、その点を「変曲点」と呼ぶ。変曲点は極大・極小とはまた別の概念である。は、極小である場合と極大である場合とどちらでもない場合があり得る（上図の右側ではどちらでもない場合のみを描いている）二階微分が0で極小である例としては$\ycol{y}=\xcol{x}^{2n}$（$n>2$）の$\xcol{x}=0$がある。。

等周問題

　辺の長さの和が同じ長方形の中で、もっとも面積が大きいのはどんな形だろう？---このような問題を「等周問題」と言う。これのもっとも簡単な問題である「等しい周の長方形の中で一番面積が大きいものはなにか？」を微分を使って考えてみる。

　長方形の辺の長さの和を$4L$とする（一辺が$L$の正方形ならちょうど周の長さは$4L$であり、図に示したように横が$0.9L$になったら、縦は$1.1L$にならなくてはいけない）。横の長さを$\xcol{x}$とすると、縦の長さは$2L-\xcol{x}$となる。面積は$\rcol{S}=\xcol{x}(2L-\xcol{x})$となる。

　$\xcol{x}$は$0<\xcol{x}<2L$の範囲で意味があるから、それを定義域としてグラフを描いてみると上に描いたような中央が盛り上がった形になる（もちろん、グラフを描かなくても以下の話はわかる）。

　面積$\rcol{S}$を$\xcol{x}$で微分すると、 \begin{equation} {\ddx\rcol{S}}= 2L - 2\xcol{x} \end{equation} となり、微分（すなわち変化量）が0になるのは$\xcol{x}=L$の時、つまり正方形の時である。

　ところでこの微分も、上の図のように図解して、 \begin{equation} \rcol{\mathrm dS} = (2L-\xcol{x})\coldx - \xcol{x}\coldx \end{equation} のように考えることもできる。こうして考えておいて、「微分が0になるところは、増える部分と減る部分が同じ大きさになる時（$2L-\xcol{x}=\xcol{x}$）である」と考えると、$\xcol{x}=L$（すなわち正方形）の時が最大値であることがわかる。

スケール変化と最適サイズ

　物体のサイズを変えていったとき、いろんな量がサイズの関数として表現される。たとえば人間の身長を$\xcol{h}$とすると、体重はだいたい$\xcol{h}^3$に比例する。直方体で考えた時に体積が縦・横・高さの積で表されることを考えれば、まず体積が$\xcol{h}^3$に比例することはわかるだろう。

　また、骨が支えることができる重さは面積に比例するだろうから、$\xcol{h}^2$に比例する。

　そこで、身長を$\xcol{h}$として体重を$W=w\xcol{h}^3$（$w$は定数）と書き、その人の足が支えることができる重さを$B=b\xcol{h}^2$（$b$は定数）と書こう。$B$よりも足に掛かる力が強くなったら足の骨が折れる、と考える。すると、持つことができる荷物の重さは（自分の体重の分は引いておかなくてはいけないので）$C=B-W=b\xcol{h}^2-w\xcol{h}^3$となる。

　ここで、体重は三乗に比例し、支えることのできる重さは二乗に比例し、と冪が違うこと、つまり「スケール変化による変数の変化の仕方に違いがあること」に注意しておこう。$\xcol{h}$が小さい領域では二乗と三乗では二乗の方が大きいが、$\xcol{h}$が大きい領域では逆転する。$\xcol{h}$があまり大きすぎると、足が支えられる体重よりも自分の体重の方が重い（立っていられない）という状況が出現する。自然現象の起こるスケールというのは、このように異なるスケール変化をする変数の間の「せめぎあい」で決まる。

　実例として人間の身長が妥当なものかどうかを検討しよう。簡単のため、\talk{標準人間}として「身長2 mで体重100 kg、200 kgの荷物を持って立つことができる人」（通常の３倍までの重力がかかったと仮定しても耐えられる人、と考えてもよい）を設定しよう。すると、$100=8w$より、$w=12.5$であり、$200=4b-100$より、$b=75$である。他の人間は全て標準人間のサイズを変化させたものだとしよう（もちろんこの仮定はむちゃくちゃであるが、「第一近似」としてよいことにしよう）。

標準人間および標準人間をスケール変化させた人間に対しては、持つことができる荷物の重さは$C=75\xcol{h}^2-12.5\xcol{h}^3$という式で書ける。これからすると、もっとも重い荷物が持てるのは、 \begin{equation} {\mathrm dC\over \mathrm dh}=150\xcol{h}-37.5\xcol{h}^2=0~~~より~~~\xcol{h}={150\over 37.5}=4 \end{equation} で、$\xcol{h}=4$（身長4 m）の人である。

　どんどん巨大になれば持てる荷物も増えるのかというとそうではない。右でグラフで示したように、体重の増加（三乗比例）はいずれ支えることができる重さ（二乗比例）に勝ってしまう。だからある身長（$\xcol{h}=6$）より高いとそもそも立っていられない。そして、保持できる荷物の重さには最大値がある（それが$\xcol{h}$の最適値であるとも言える）。

　実際二足歩行する動物のサイズがせいぜい2 mぐらいなのは、ここで行った計算がだいたい正しいことを示している（立って荷物を持つだけでなく、走ったりして動きまわらなくてはいけないのだから、ある程度余裕を持たせておかないといけない）。

体積最大の箱を作る

図のように、一辺$A$ cmの正方形の紙から、一辺$\xcol{x}$ cmの正方形を4つ切り出して、折り曲げて蓋なしの箱を作った（のりしろは適当につけたものとする）。 この箱の容積を最大にする$\xcol{x}$の値を求めよ。

底面は一辺$A-2x$の正方形になる。高さが$x$であるとして箱の容積は${V}=\xcol{x}(A-2\xcol{x})^2$である。微分すると、${\mathrm dV\over \coldx}=(A-2\xcol{x})^2+2\xcol{x}(A-2\xcol{x})\times(-2)=(A-2\xcol{x})(A-2\xcol{x}-4\xcol{x})=(A-2\xcol{x})(A-6\xcol{x})$となる。${V}$の微分が0になるのは$\xcol{x}={A\over 2}$と${A\over 6}$である。$\xcol{x}={A\over 2}$では体積が0になってしまうから、最大値になるのは$\xcol{x}={A\over 6}$である。

ラグビーのキック

ラグビーでトライ成功した後のキックは、トライ地点からタッチラインに平行に伸ばした線の上であればどこで蹴ってもよいことになっている。では、どの位置から蹴ると、蹴る人から見た２本のゴールポストの間の角度は最大になるか。図のような配置の場合で考えよ。

なお、本当は遠いと蹴るのがたいへんという要素も考えて最適を考えなくはいけないが、ここでは「見たときの角度」の大小のみを考えることにする。

　角度は$\arctan\left({d+L\over \xcol{x}}\right)-\arctan\left({d\over \xcol{x}}\right)$となるから、これを$\xcol{x}$で微分する。 \begin{equation} \begin{array}{rl} &\ddx\left(\arctan\left({d+L\over \xcol{x}}\right)-\arctan\left({d\over \xcol{x}}\right)\right)\\[2mm] =&{1\over 1+\left({d+L\over \xcol{x}}\right)^2}\times\left(-{d+L\over \xcol{x}^2}\right) -{1\over 1+\left({d\over \xcol{x}}\right)^2}\times\left(-{d\over \xcol{x}^2}\right) \\ \end{array} \end{equation} これを整理すると、 \begin{equation} {L(-\xcol{x}^2+d^2+dL)\over \xcol{x}^4\left(1+\left({d+L\over \xcol{x}}\right)^2\right)\left(1+\left({d\over \xcol{x}}\right)^2\right)} \end{equation} となるから、極大もしくは極小となるのは$\xcol{x}^2=d^2+dL$になるとき。$\xcol{x}$は正だから、$\xcol{x}=\sqrt{d^2+dL}$のとき最大値となる。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。