テイラー展開
関数の近似とテイラー展開
関数の近似
近似とはすなわち「真実の値とは少し違うが、だいたい等しい数値を求める」という方法である。
と、思う人が多い。「科学ともあろうものが『だいたい』なんていいかげんなことでよいのか?」と憤慨する人もいる。しかし、実際にはいろんな理由で近似が必要となる。まず、
ということが大きい。高校までの勉強では(大学でも低学年でなら)ほぼ、「解ける問題」しか出てこない。ところが世の中には「解けない問題」はいくらでもある。高校および大学初年度程度の教科書は「解ける問題」を厳選して載せている。では解けない問題が出てきたらどうするかと言えば、「頑張って解く方法を見つける(見つからないかもしれない)」か、「近似してから解く」しかない。
もう1つここで言っておきたいことは、真面目に解くことはほんとに必要か?ということである。たとえば(あくまで「たとえば」)近似しないで真面目に解いた場合の答と、近似した結果の答が0.1%(つまり${1\over 1000}$ぐらい)違っていたとしよう。その${1\over 1000}$の違いが大きな問題になる時もあれば、そうでない時もある。たとえば今最小目盛りが1mmである物差しで20cmぐらいの長さを測定したとしたら、この測定では$\textstyle {1\over 200}$より細かい精度の数字は得られていない。そういう測定で「近似したら${1\over 1000}$ぐらい答がずれる!」にこだわることは果たして必要だろうか?---近似してよいかまずいかは、要求されている精度によって決まるものである。
近似としてもっとも大雑把なものは関数$\ycol{y}=f\kakko{\xcol{x}}$を$\ycol{y}=f\kakko{x_0}$で代用するというものである。つまり$\xcol{x}$を変えても$\ycol{y}=f\kakko{\xcol{x}}$はそんなに変わらないだろうと推測する。こういう近似をやっている例を上げると
という推測である「関数を定数で代用する」と聞くととんでもないことをやっているように思えるかもしれないが、この例のように「そんなに大きく変わるものではない」がわかっている量については、普段からよくやっている。実際には場所によって違う地球の重力加速度を、$g$という定数で置き換えるのもその例である。。
もう少しまじめに関数を近似するのが「線形近似(linear approximation)」である。「線形(linear)」この場合に限らず、1次式で書けるという性質を「線形」と表す。英語から「リニア」という言い方もする。というのは「グラフで描くと直線になる」という意味で、($\ycol{y}=a\xcol{x}+b$のような)1次式で書けることである(微分のところでは「微小な範囲を考える(グラフを拡大する)」ことで線形近似できる形に持っていった)。つまりは線形近似とは「1次式で近似する」もしくは「グラフが直線だと近似する」ことになる。たとえば「朝9時の気温が20度で、10時の気温が22度だから、11時の気温は24度だろう」という推測は線形近似である。あくまで近似であるから、推測が当たる時もあるし、当たらない時もあるだろう。「この人は100mを12秒で走れるから、200mは24秒で走れるだろう」というのも線形近似に基づく推測だが、これには当然、「人間は疲れるのでは?」という反論があってしかるべきである。
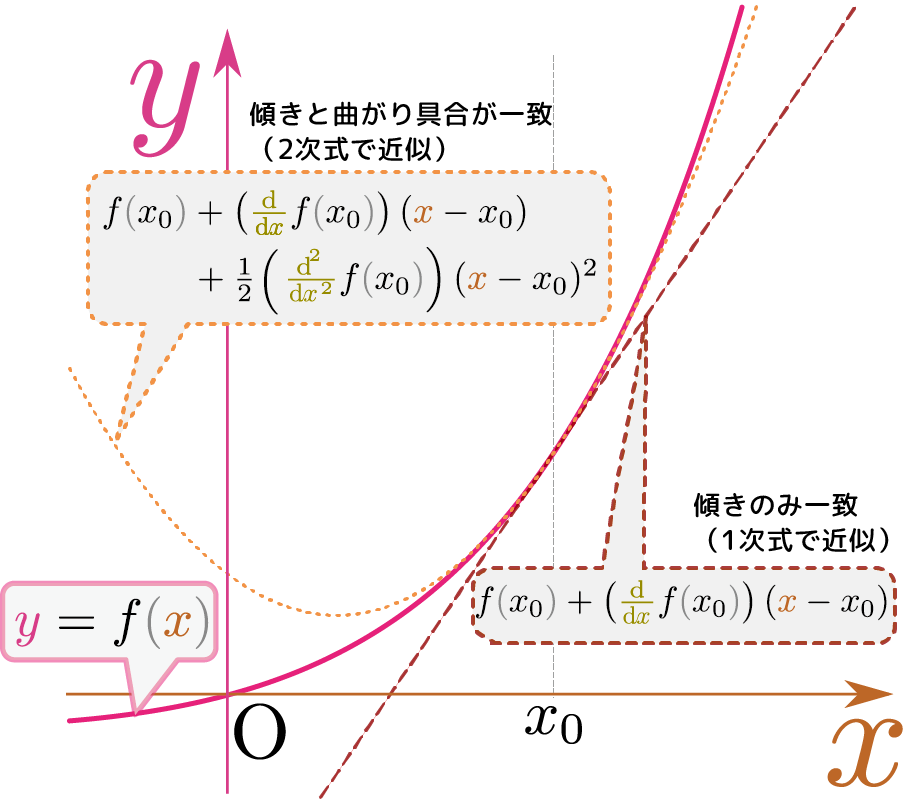
微分というのはいろんな関数$\ycol{y}=f\kakko{\xcol{x}}$を「拡大してみれば(あるいは、狭い範囲だけに注目すれば)直線$\ycol{y}=a\xcol{x}+b$のようなものだ」と大まかな近似として表した時の傾き$a$である、と言える。
微分の表現:$f\kakko{\xcol{x} + \xcol{\Delta x}}\simeq f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\xcol{\Delta x}$を思い出し、$\xcol{x}\to x_0,\xcol{\Delta x}\to \xcol{x}-x_0$と置き直すと、 \begin{equation} f\kakko{\xcol{x}}\simeq f\kakko{x_0}+\left( \ddx f\kakko{x_0}\right)(\xcol{x}-x_0) \end{equation} ということになるこの$\ddx f\kakko{x_0}$は「関数$f\kakko{\xcol{x}}$を$\xcol{x}$で微分した後に$\xcol{x}$に$x_0$を代入したもの」という意味である(先に代入してしまったら微分すると0である)。すでに代入が終わっているので、この後$\xcol{x}$で微分すると0になる。釈然としない人がいるかもしれないが、これはそういう書き方をするのが(式を簡単に書くための)決め事なのだと思ってほしい。。この式は$\xcol{x}=x_0$を代入すると$f\kakko{x_0}=f\kakko{x_0}$となって成り立つし、$\xcol{x}$で微分してから$\xcol{x}=x_0$を代入しても成り立つ。しかしこれだと、$\xcol{x}$で二階微分すると等式は成り立たない(右辺は0になってしまうが左辺はそうとは限らない)。 \begin{equation} f\kakko{\xcol{x}}\simeq f\kakko{x_0}+\left( \ddx f\kakko{x_0}\right)(\xcol{x}-x_0)+{1\over 2}\left( \left(\ddx\right)^2 f\kakko{x_0}\right)(\xcol{x}-x_0)^2 \end{equation} と新しい項を付け加えることで二階微分も等しくする。右辺を二階微分すると、第1項と第2項は0になり、第3項の${1\over 2}(\xcol{x}-x_0)^2$の二階微分は1になるので、結果は$\left(\ddx\right)^2f\kakko{x_0}$となり$\left(\ddx\right)^2f\kakko{x_0}$は「微分した後$\xcol{x}=x_0$を代入した結果」なのでもう$\xcol{x}$の関数ではないことに注意。、左辺の二階微分の$\xcol{x}=x_0$での値と一致する(こうなるように${1\over 2}$という係数を選んでおいた)。
関数の値(零階微分)と一階微分、二階微分が一致するのだから、より本当の関数に近づいている(ここまでで「関数$f\kakko{\xcol{x}}$を2次式で近似する」ということができた)。この要領でどんどん右辺を左辺に近づけていく。この次の段階では、三階微分が等しくなるように、右辺に${1\over 3\times 2}\left(\left(\ddx\right)^3f\kakko{x_0}\right)(\xcol{x}-x_0)^3$を足す。以下同様に考えて、左辺と右辺で$\xcol{x}=x_0$での値$f\kakko{x_0}$と任意の階数の導関数$\left(\ddx\right)^nf\kakko{x_0}$が一致するようにすると、「テイラー展開(Taylor expansion)」と呼ばれる特に$x_0=0$の場合には「マクローリン展開」という別の名前がついているが、わざわざ別の名前にするほどの意味はない。以下の式を作ることができる。
テイラー展開
\begin{equation} f\kakko{\xcol{x}}= \sum_{n=0}^\infty {1\over n!}\left(\left(\ddx\right)^nf\kakko{x_0}\right)(\xcol{x}-x_0)^n\label{taylorexp} \end{equation}
以上の計算が実行できるような関数は「$\xcol{x}=x_0$において「解析的(analytic)」である」と言う。解析的であるためには、ある領域で何回でも微分可能という条件が成り立たなくてはいけない(さらに級数が収束$\sum_{n=0}^\infty$のような足算(これを「級数」と呼ぶ)の結果が特定の値に収まる(計算可能である)ことを「収束する」と表現する。収束しない場合を「発散する」と表現する。することも必要)。テイラー展開はこの条件のもとで考えている。このような「何回でも微分可能な関数」のことは「なめらかな関数」と呼ぶ。
また、$n$が整数でない場合、$(\xcol{x}-x_0)^n$を$m$階微分すると$(\xcol{x}-x_0)^{n-m}$に比例し、これは$n-m<0$になるとこの点で定義されない($n$が正の整数なら負になる前に0になるから問題ない)。つまり$n$が0以上の整数でないならどこかで微分不可能になってしまう。「どこかで微分が不可能になるような関数」を展開しなくてはいけない状況が来たら、その時は$n$が0以上の整数でないような展開も出現するだろう。
ここで、のアプリでいろんな関数のテイラー展開の様子を見た。
テイラー展開の例:等比級数になる例
テイラー展開の例として、${1\over 1-\xcol{x}}$という関数のテイラー展開を考えよう。なぜこれを考えるかというと、この関数の「ある条件の元での展開」は微分を使わなくても出せる(よって、後で微分を使って出した展開式と比較できる)からである。というのは初項1、公比$\xcol{x}$の等比数列の和は \begin{equation} {1-\xcol{x}^{N}\over 1-\xcol{x}}= 1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\xcol{x}^4+\xcol{x}^5+\cdots+\xcol{x}^{N-1}=\sum_{n=0}^{N-1} \xcol{x}^n\label{touhix} \end{equation} になるという公式がある$( 1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\cdots+\xcol{x}^{N-1})(1-\xcol{x})$を計算すれば、$1-\xcol{x}^N$になることから導ける。。この式は \begin{equation} {1\over 1-\xcol{x}}=1+\xcol{x}+\xcol{x}^2+\cdots + \xcol{x}^{N-1} + \underbrace{ {\xcol{x}^N\over 1-\xcol{x}} }_{剰余項}\label{oneoverjouyo} \end{equation} と表すこともできる。「剰余項」と示した部分は、${1\over 1-\xcol{x}}-{1-\xcol{x}^N\over 1-\xcol{x}}$という計算の結果である。
$|\xcol{x}|<1$であれば、$\lim_{N\to\infty}\xcol{x}^N=0$になるから、$N$を$\infty$にすることで、 \begin{equation} {1\over 1-\xcol{x}}= 1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\xcol{x}^4+\xcol{x}^5+\cdots=\sum_{n=0}^\infty \xcol{x}^n\label{oneminux} \end{equation} を得る。この式はテイラー展開の式の形になっている。というのは、 \begin{equation} \ddx \left({1\over 1-\xcol{x}}\right)={1\over (1-\xcol{x})^2},~~~ \ddx \left({1\over (1-\xcol{x})^2}\right)={2\over (1-\xcol{x})^3},~~~ \ddx \left({2\over (1-\xcol{x})^2}\right)={2\times 3\over (1-\xcol{x})^4},\cdots \end{equation} のように順に計算していくと \begin{equation} \left(\ddx \right)^n \left({1\over 1-\xcol{x}} \right)= n! \left({1\over 1-\xcol{x}}\right)^{n+1}\label{tayloronex} \end{equation} であることがわかり、この式に$\xcol{x}=0$を代入すると答えは$n!$となり、テイラー展開の公式に入れれば${1\over 1-\xcol{x}}=\sum_{n=0}^\infty \xcol{x}^n$という式が成立するからである。ところが、上で$N\to\infty$の極限を取ったときに$\xcol{x}^N\to0$となるのは(級数の和を${1\over 1-\xcol{x}}$にできるのは)$|\xcol{x}|<1$の時だけである。つまりこの式が成立するのは、$-1<\xcol{x}<1$という範囲だけなのだ。
このあたりはアプリの画像を見ながら納得して欲しい。
$\xcol{x}=1$が「ここを超えるとテイラー展開できない点」になるのは考えてみればあたりまえで、そもそもテイラー展開の式は一階微分から初めて$n$階微分による影響を計算していくことで関数の値を求めようというものであるが、$\xcol{x}=1$のところで関数$f\kakko{\xcol{x}}={1\over 1-\xcol{x}}$は定義されておらず不連続で微分もできないから、「微分を使って値を求める」という計算であるテイラー展開が破綻するのは当たり前である「公式や定理は適用限界を超えて使ってはならない」を教訓として心に刻んでおこう。運良くそれでも大丈夫な場合もあるかもしれないが、確認は必要である。。実際、$\xcol{x}>1$の範囲では${1\over 1-\xcol{x}}$は負にならなくてはいけないが、$1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\xcol{x}^4+\xcol{x}^5+\cdots$は正にしかなりえず、この範囲では負の値を採っている${1\over 1-\xcol{x}}$に近づくことはない。
一方、$1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\xcol{x}^4+\xcol{x}^5+\cdots$という式は$\xcol{x}=-1$の時は \begin{equation} \underbrace{\underbrace{1-1+1-1+1-1}_{ここまでの和は0}+1}_{ここまでの和は1}-1+1-1+1-1+\cdots \end{equation} のような式となり、奇数個の項があると答は1、偶数個の項があると答は0、と$1$と$0$を振動している(グラフを見てもわかる)。一方、大本の${1\over 1-\xcol{x}}$は$\xcol{x}=-1$ではその中間である${1\over 2}$になる。
テイラー展開は、「どの範囲までが展開可能なのか」を正しく判断しないと間違えた展開の仕方をしてしまうことに注意しよう。
テイラー展開の例:指数関数
指数関数$\ycol{y}=\E^{\xcol{x}}$の場合は、微分しても微分しても$\E^{\xcol{x}}$のままであり、$\xcol{x}=0$での値は1だから、$\left(\ddx\right)^n f\kakko{x_0}$のすべてに1を代入して、 \begin{equation} \E^{\xcol{x}}=\sum_{n=0}^\infty {1\over n!}\xcol{x}^n =1+\xcol{x}+{\xcol{x}^2\over 2!}+{\xcol{x}^3\over 3!}+{\xcol{x}^4\over 4!}+{\xcol{x}^5\over 5!}+\cdots =\sum_{n=0}^{\infty}{1\over n!}\xcol{x}^n\label{exptaylor} \end{equation} というテイラー展開になる。
テイラー展開の例:三角関数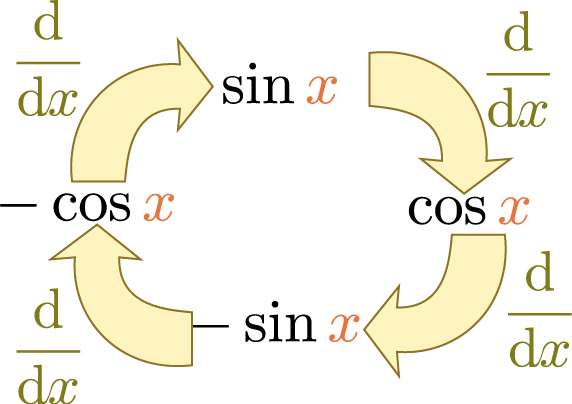
$\sin \xcol{x}$を例にして考えよう。すでに述べたように、$\sin \xcol{x}$は$\xcol{x}=0$で0であり、傾き1である。よって$\sin \xcol{x} \simeq \xcol{x}$と書けるのであった。$\sin \xcol{x}$の一階微分は$\cos \xcol{x}$、二階微分は$-\sin \xcol{x}$である。三階微分は$-\cos \xcol{x}$となり、微分するごとに$\sin \xcol{x}\to\cos\xcol{x}\to -\sin\xcol{x}\to -\cos\xcol{x}\to \sin \xcol{x}$と4つの関数をぐるぐる回る。分類すれば、 \begin{equation} \left(\ddx\right)^n \sin \xcol{x}= \begin{cases} \sin\xcol{x}& n=4m\\ \cos\xcol{x}& n=4m+1\\ -\sin\xcol{x}& n=4m+2\\ -\cos\xcol{x}& n=4m+3 \end{cases}~~~(mは0以上の整数)\label{sindiffn} \end{equation} であり、これに$\xcol{x}=0$を代入すれば \begin{equation} \left(\ddx\right)^n \sin \xcol{x} \biggr|_{\xcol{x}=0}= \begin{cases} 0& n=2m\\ 1& n=4m+1\\ -1& n=4m+3 \end{cases}~~~(mは0以上の整数)\label{sinexpcof} \end{equation} ($n=4m$と$n=4m+2$は一つにまとめて$n=2m$とした)であるから、 \begin{equation} \sin \xcol{x}=\xcol{x} - {\xcol{x}^3\over 3!}+ {\xcol{x}^5\over 5!}-{\xcol{x}^7\over 7!}+\cdots\label{sintaylor} \end{equation} のようにテイラー展開できる偶数次の項が出てこないのが$\sin$の特徴であるが、$\sin$に限らず奇関数なら常に奇数次しか出てこない。ただし、$\xcol{x}=0$以外で展開した場合はこの限りではない。。
一方、同様の計算をやると$\cos\xcol{x}$の方は \begin{equation} \cos \xcol{x}=1 - {\xcol{x}^2\over 2!}+ {\xcol{x}^4\over 4!}-{\xcol{x}^6\over 6!}+\cdots\label{costaylor} \end{equation} のようにテイラー展開できる($\cos$では奇数次の項が出てこない偶関数の$\xcol{x}=0$の周りのテイラー展開では常に、偶数次の項のみが出てくる。)。
$\exp$の展開と、$\sin $の展開と$\cos $の展開をよく見ると、 \begin{equation} \begin{array}{ccccccccc} \E^{\xcol{x}}= &1 &+\xcol{x} &+{\xcol{x}^2\over 2!} &+{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+{\xcol{x}^5\over 5!} &+{\xcol{x}^6\over 6!} &+\cdots \\[3mm] \cos \xcol{x}= &1 & &-{\xcol{x}^2\over 2!} & &+{\xcol{x}^4\over 4!} & &-{\xcol{x}^6\over 6!} &+\cdots \\ \sin \xcol{x}= & &\xcol{x} & &-{\xcol{x}^3\over 3!} & &+{\xcol{x}^5\over 5!} & &+\cdots \\ \end{array}\label{Eulercossin} \end{equation} となっている。ここで「$\cos\xcol{x}$と$\sin\xcol{x}$の展開は$\E^{\xcol{x}}$に似ているが、符号が一項ごとに反転するのが惜しいな」と気づく。$\E^{\xcol{x}}$の展開で2項ごとに符号が反転してくれれば同じものになりそうだ。そうするためには、 \begin{equation} \begin{array}{cccccccccl} \E^{\xcol{x}}= &1 &+\xcol{x} &+{\xcol{x}^2\over 2!} &+{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+{\xcol{x}^5\over 5!} &+{\xcol{x}^6\over 6!} &+\cdots &\kokode{\xcol{x}\to \I\xcol{x}}\\[3mm] \E^{\mathrm i \xcol{x}}=& 1 &+\I \xcol{x} &-{\xcol{x}^2\over 2!} &-\I{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+\I{\xcol{x}^5\over 5!} &-{\xcol{x}^6\over 6!} &+\cdots \end{array} \end{equation} のように指数に虚数単位$\I$をつければよい($\xcol{x}\to\I\xcol{x}$と置き換えればよい)と気がつけば、 \begin{equation} \E^{\mathrm i \xcol{x}}=\cos \xcol{x}+\I \sin \xcol{x}\label{Euler} \end{equation} という「オイラーの関係式」が見えてくる。
テイラー展開可能な点と不可能な点
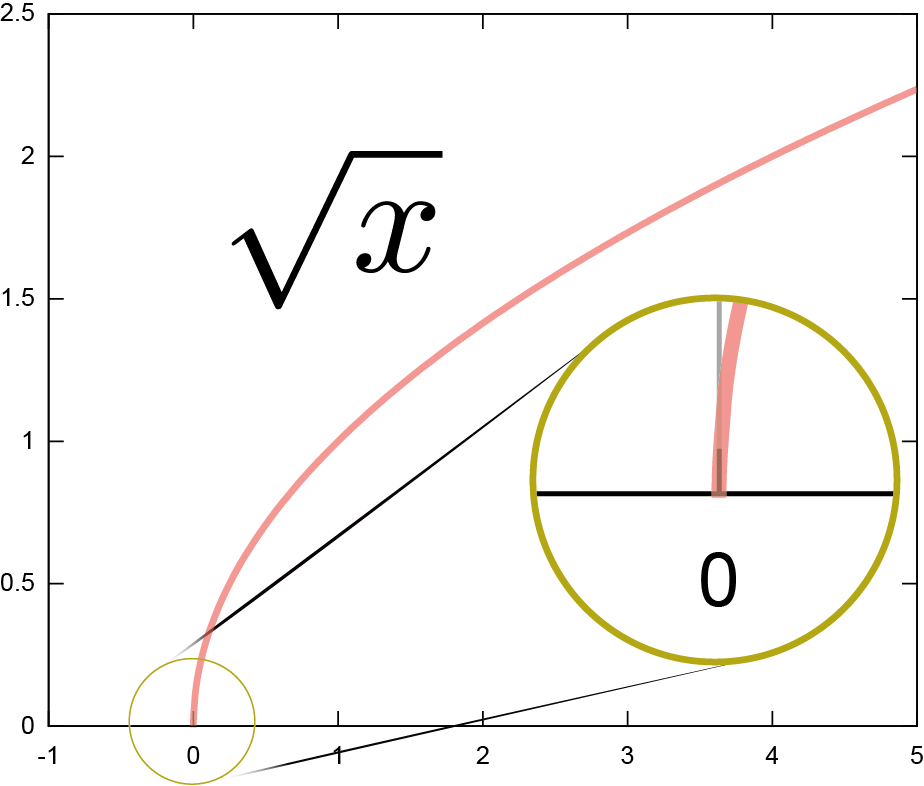
テイラー展開が可能であるためには、$f\kakko{x_0}$はもちろん、任意の階数の微係数$\ddx f\kakko{x_0},\left(\ddx\right)^2f\kakko{x_0},\cdots$が全て計算できなくてはいけない。たとえば、$f\kakko{\xcol{x}}=\sqrt{\xcol{x}}$を$\xcol{x}=0$の周りにテイラー展開することはできない(この関数は$\xcol{x}=0$において解析的でない)。$\ddx f\kakko{\xcol{x}}={1\over 2\sqrt{\xcol{x}}}$なので、$\xcol{x}=0$では微分が存在しない(あえて書くなら$\infty$)。グラフでは、$\xcol{x}=0$において線が垂直に立っていることで「微分できない」ことが表現されている。
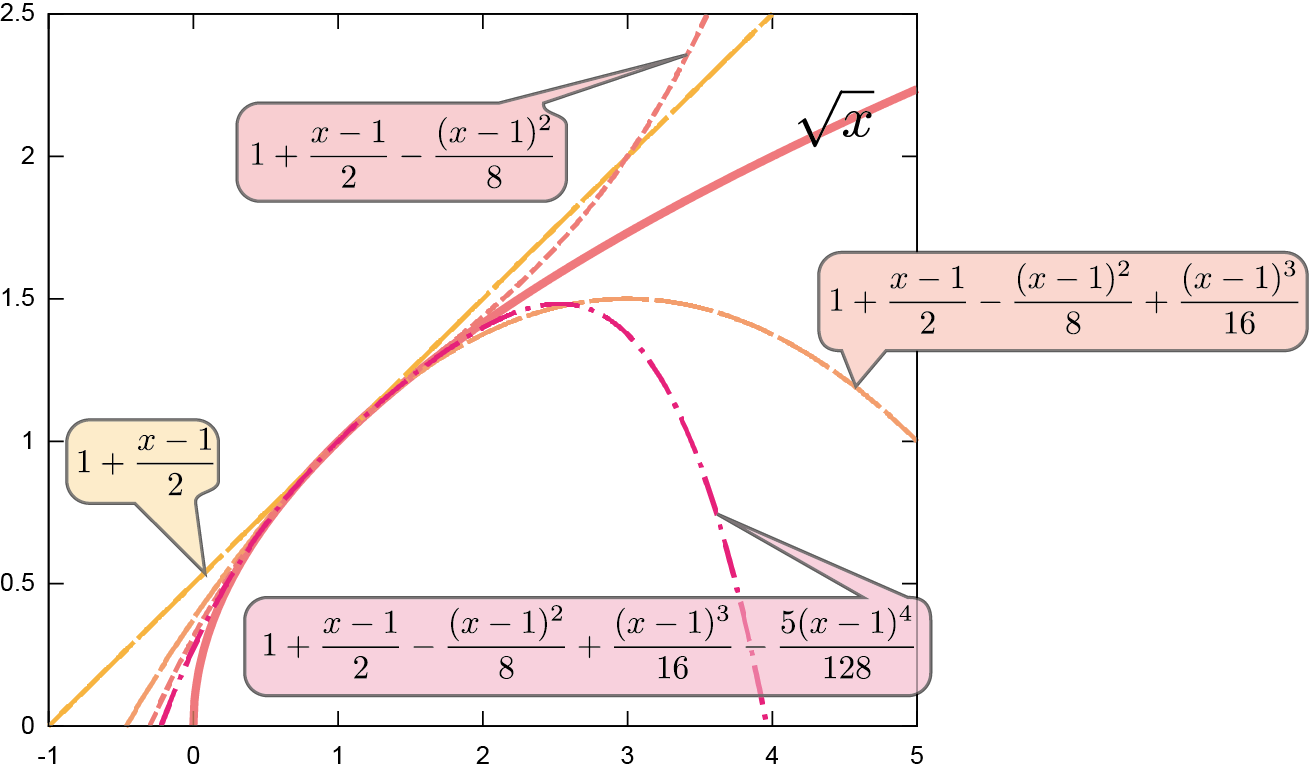
では$\sqrt{\xcol{x}}$のような関数はどうやって近似するかというと、$\xcol{x}=0$以外、たとえば$\xcol{x}=1$の周りにテイラー展開する。$\xcol{x}=1$でなら、${1\over 2\sqrt{\xcol{x}}}\biggr|_{\xcol{x}=1}={1\over 2}$となって値がある。二階微分も計算しておくと、$\left(\ddx\right)^2\sqrt{\xcol{x}}=-{1\over 4\xcol{x}^{3\over 2}}$となるから2次の項の係数は${1\over 2}\left(\ddx\right)^2\sqrt{\xcol{x}}\biggr|_{\xcol{x}=1}=-{1\over 8}$であり(3次以上の項については詳細は省くが同様の計算を行って)、 \begin{equation} \sqrt{\xcol{x}}= 1 +{1\over 2}(\xcol{x}-1)-{1\over 8}(\xcol{x}-1)^2+{1\over 16}(\xcol{x}-1)^3-{5\over 128}(\xcol{x}-1)^4+\cdots \end{equation} のように展開できる。たとえば電卓を叩けば$\sqrt{1.2}\fallingdotseq1.09544511501033\cdots$という式が出るが、電卓内部では上のような展開を使って計算される。やってみると、 \begin{equation} \sqrt{1.2}= \underbrace{\underbrace{\underbrace{\underbrace{1 +\underbrace{{1\over 2}(1.2-1)}_{0.1}}_{1.1}-\underbrace{{1\over 8}(1.2-1)^2}_{0.005}}_{1.095}+\underbrace{{1\over 16}(1.2-1)^3}_{0.0005}}_{1.0955}-\underbrace{{5\over 128}(1.2-1)^4}_{0.0000625}}_{1.0954375}+\cdots \end{equation} のようにして正しい値に近づいていく。下のグラフを参照せよ。
公式どおりにいかない例の一つとして、$f\kakko{\xcol{x}}=\E^{-{1\over \xcol{x}^2}}$という関数を考えよう。この関数は$\xcol{x}=0$での値は定義されていないが、
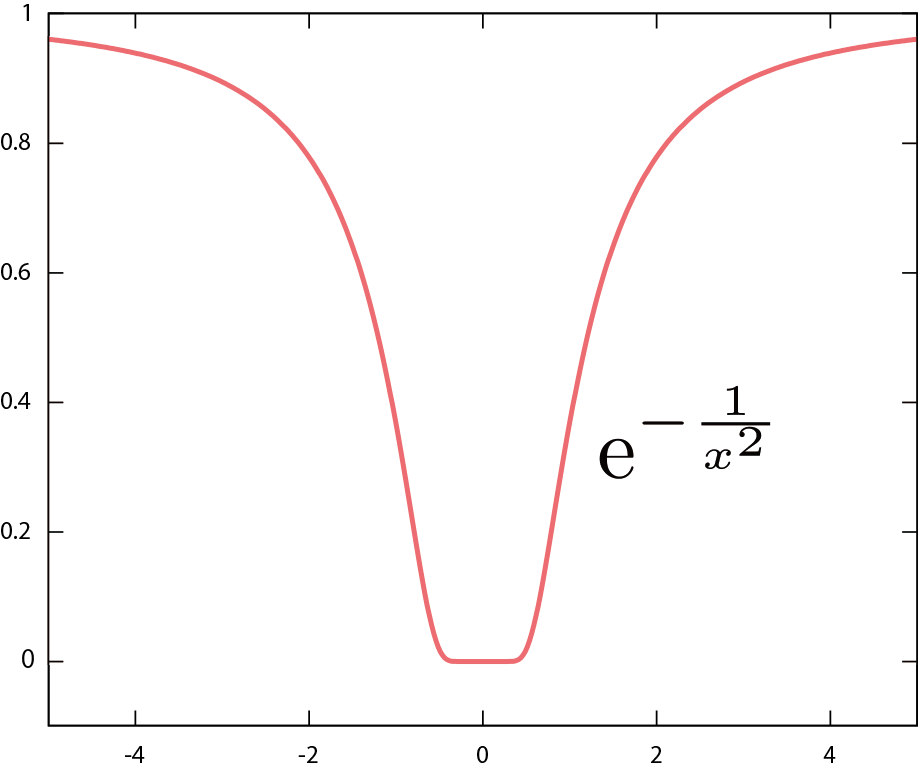
のグラフに描いたように、$\xcol{x}=0$の付近では$0$に近づく($\E^{-\infty}$だと思えばよい)ので、$f\kakko{0}=0$と定義しておくことにすれば$\xcol{x}=0$でも定義された連続した関数になる。
さらに、グラフで$\xcol{x}=0$付近が水平線になっていることからわかるように、$n$階微分しても$\left(\ddx\right)^nf\kakko{0}=0$である。一階微分と二階微分だけ計算しておくと、 \begin{equation} \ddx f\kakko{\xcol{x}}={2\over \xcol{x}^3}\E^{-{1\over \xcol{x}^2}},~~ \left(\ddx\right)^2f\kakko{\xcol{x}}= -{6\over \xcol{x}^4}\E^{-{1\over \xcol{x}^2}} +{4\over \xcol{x}^6}\E^{-{1\over \xcol{x}^2}},\cdots\label{eonoverxbibun} \end{equation} のようになるが、$\xcol{x}=0$に近づけると$\E^{-{1\over \xcol{x}^2}}$が非常に早く0に近づくので、これらはすべて0となる。よって、テイラー展開の右辺が恒等的に($\xcol{x}$によらず)0になってしまう。