変分原理と変化の向き

変分原理

　「変分原理」とは「何か基本的な量の変化を考えることで法則を導く原理」ということで、多くの場合ある量の変化量が0になるところを求めるとそれが求めたい状態であるという形で使う。

　変分原理は解析力学でも「作用が停留するのが実現する運動である」という形で使った。あるいは静力学でも「エネルギー最低の位置が安定点である」という考え方で使う。

静力学の場合

　解析力学までいくと説明することが多くなるので、静力学の場合で考えよう。無重力状態でバネ定数$k$のバネにつながれた物体を考えると、弾性力の位置エネルギー${1\over 2}kx^2$（$x$は自然長からの伸び）だから、これが最小になるのは$x=0$の点（自然長のとき）である。

　ここに重力があるとすると、重力の位置エネルギー$mgx$が加わる（$x$が上向き、つまり$x$が増加すると位置エネルギーが増える方向の座標だったとしよう）。このときは全位置エネルギーは$U={1\over2}kx^2+mgx$だから、これが最小になるのは${\mathrm dU\over\mathrm dx}=kx+mg$が0になるところだから、$x=-{mg\over k}$のところである。

もちろん、↑の計算は「弾性力$kx$と重力$mg$がつりあうところ」として求めてもよい。位置エネルギーの停留場件とつりあい条件は物理的に同じことを意味する。

　もし今位置エネルギー最小の点（$x=-{mg\over k}$）じゃない場所に物体がいたとしたら、その場所へ向かう方向に力が働き、（摩擦などによるエネルギーの散逸を得て）位置エネルギー最小点に落ち着くだろう。

　熱力学でも$U$や$F$などのエネルギーを最小化する方向へ変化が起こるという考え方で物理現象を予言しよう、というのが変分原理である。

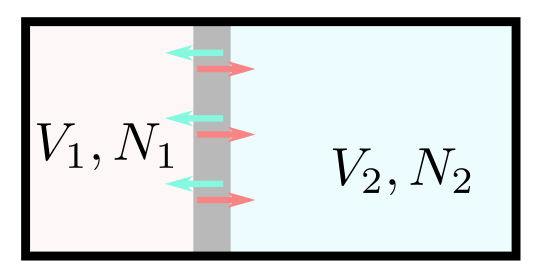
　平衡状態にある二つの系$(T;V_1,N_1)$と$(T;V_2,N_2)$を接触させて壁を取り除いてしばらく待つと、$(T,\underbrace{V_1+V_2}_V,\underbrace{N_1+N_2}_N)$という平衡状態に達する（温度は最初から同じであったことに注意）。

　このとき、ヘルムホルツの自由エネルギーの差

$$ F[T;V_1,N_1]+F[T;V_2,N_2]-F[T;V,N] $$

を考えると、これはこの変化を行った時の最大仕事である。しかし最大仕事が行われるのは準静的な操作の時で、単に壁を取り除くという操作は準静的ではないからその時の仕事は最大仕事ではない。壁を取り除いただけでは何も動かしたりしないから、仕事は0である。最大仕事は0よりは大きいことだけはわかるから、

$$ F[T;V_1,N_1]+F[T;V_2,N_2]-F[T;V,N]\geq 0 $$

という不等式を満たす。つまり

$$ F[T;V_1,N_1]+F[T;V_2,N_2]\geq F[T;V,N] $$

で、「壁を取り払って（たとえば）気体を混ぜてしまうと、ヘルムホルツ自由エネルギーは減る（か変化しない）」ということがわかる。

　二つの系が物質量$N$のやりとりができる状況にしてみよう（具体的には、壁に穴を開けて空気分子などが行き来できるようにする）。すると、最初$N_1,N_2$だった物質量が、$\tilde N_1,\tilde N_2$（もちろん、$N_1+N_2=\tilde N_1+\tilde N_2=N$）になったところで平衡に達したとしよう。この時もヘルムホルツ自由エネルギーは減る（か、変化しない）はずで、逆に言えば「もう減らせない」というところで変化が止まるはず、と考えると、

$$ F[T;V_1,\tilde N_1]+F[T;V_2,\tilde N_2]=\min_{N_1,N_2\atop N_1+N_2=N}F[T;V_1,N_1]+F[T;V_2,N_2] $$

が成立するだろう（最小値が一個じゃない場合については後で考える）。

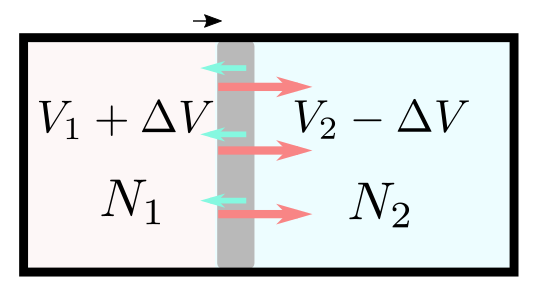
　体積がやりとりされる（間の壁が押されて動くような状況）についても同様に、

$$ F[T;\tilde V_1,N_1]+F[T;\tilde V_2,N_2]=\min_{V_1,V_2\atop V_1+V_2=V}F[T;V_1,N_1]+F[T;V_2,N_2] $$

が成立する。

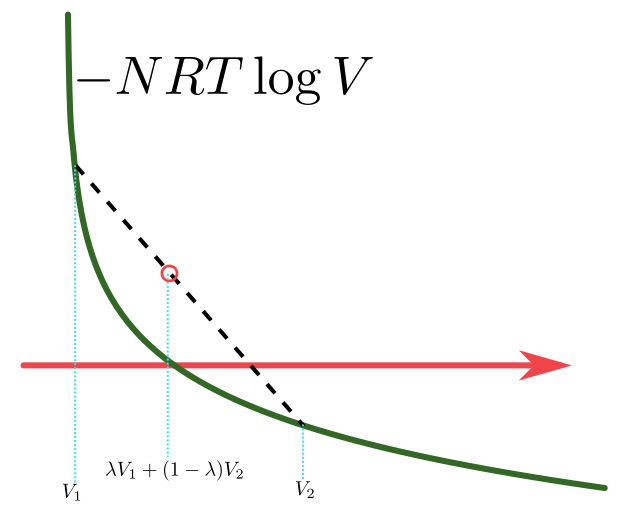
　理想気体の場合、$F=-NRT\log V+(Vに依らない部分)$だから、 $$ F[T;V_1,N_1]+F[T;V_2,N_2]=-N_1 RT \log V_1 -N_2 RT \log V_2 + (V_1,V_2に依らない部分) $$ という式で書ける。

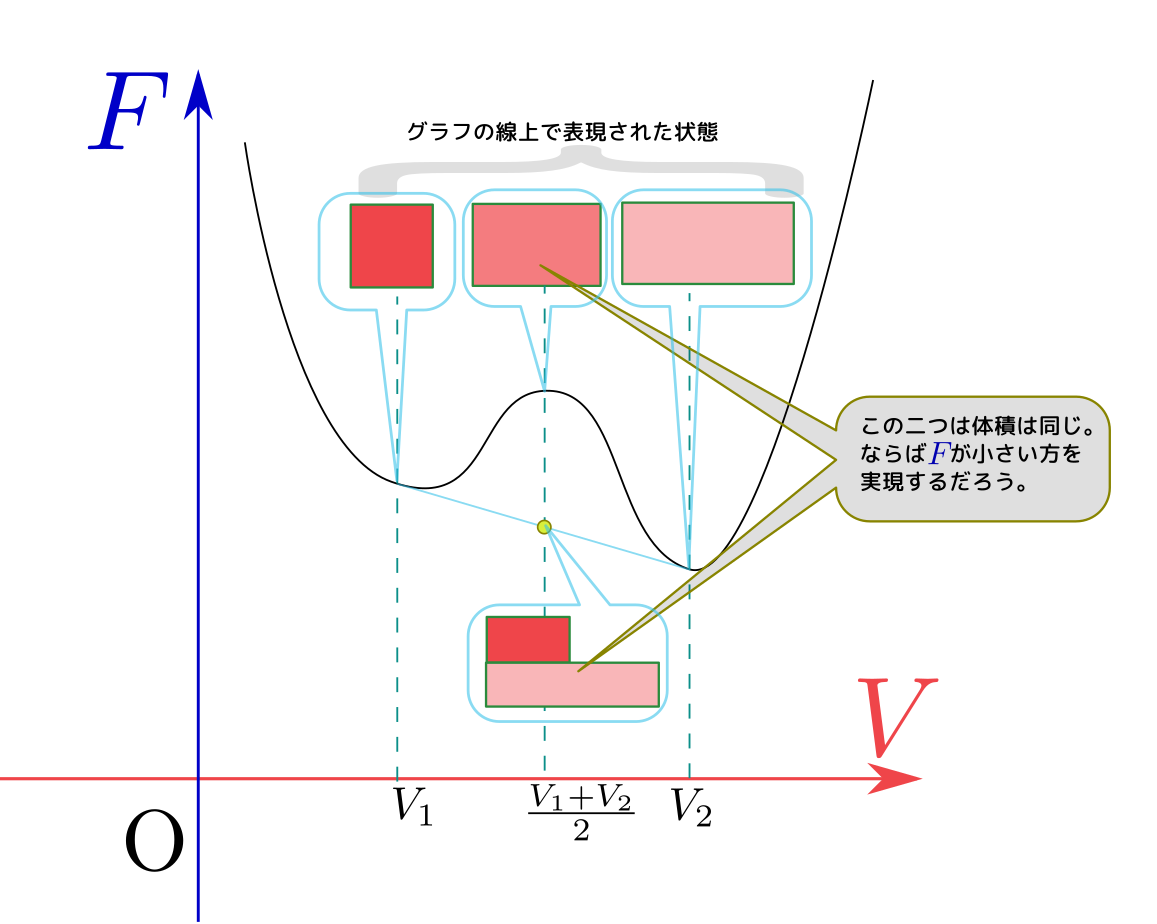
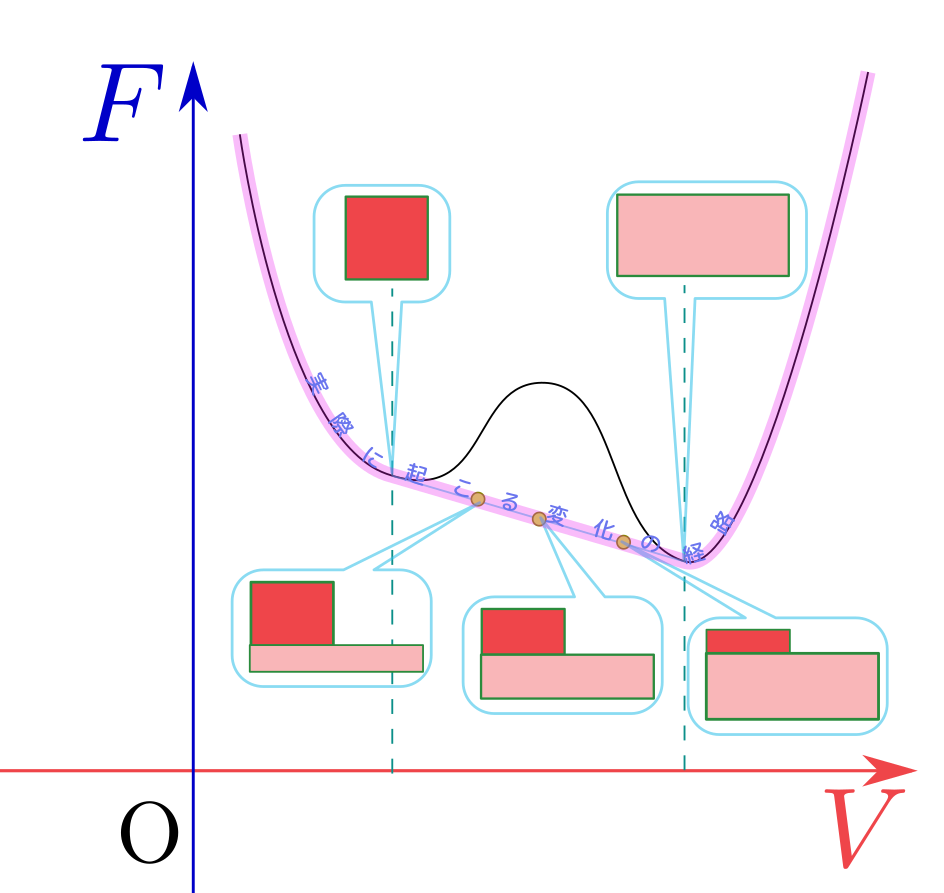
　$V_2=V-V_1$としてグラフを描くと

となって、どこかに最小値が確かにある（具体的計算とその意味は後で）。

熱力学関数の凸性

熱力学関数の凸性

ヘルムホルツの自由エネルギーの凸性

　以上のように「二つの系を合体させると$F$は減るはず」という原理から、$F$という関数は、 $$ F[T;\lambda V_1+(1-\lambda)V_2,\lambda N_1+(1-\lambda)N_2]\leq \lambda F[T;V_1,N_1]+(1-\lambda) F[T;V_2,N_2] $$

という不等式を満たす。$(T;\lambda V_1+(1-\lambda)V_2,\lambda N_1+(1-\lambda)N_2)$とは、$(T;V_1,N_1)$と$(T;V_2,N_2)$を$\lambda:1-\lambda$に内分した点である。単純な例として$\lambda={1\over2}$の場合を考えればこれは $$ F[T;{V_1+V_2\over2},{N_1+N_2\over 2}]\leq {F[T;V_1,N_1]+F[T;V_2,N_2]\over2} $$ で、「中点での$F$は両端の平均より小さい」ということを意味している。

　実例として理想気体の場合、$F=-NRT\log V+$（$V$によらない部分）となっているが、$-NRT\log V$のグラフは下に凸である。

　ヘルムホルツ自由エネルギーが「下に凸（）」でなかったらどういうおかしいことが起こるかを一つの例で示そう。

　上のような「下に凸でない」$F$が存在したとしよう。すると明らかに、$F[T,{V_1+V_2\over2}]$より、$F[T,V_1]+F[T,V_2]\over2$の方が小さい。

　つまり同じ${V_1+V_2\over2}$という体積を占める状態であれば、${V_1\over2},{V_2\over2}$という体積を持った二つの状態に別れた方が、ヘルムホルツ自由エネルギーが小さくなる（この例は中点で見せたが、$\lambda:1-\lambda$で内分した点でも同様のことが言える）。

　このような場合、実際に起こるのは↓のような変化過程であろう。

実はこれが次に考える「相転移」の起こる過程である。

つりあい点

最小になる点を探すには「微分して0」を解けばよい。すなわち、 $$ {\partial\over\partial V_1}\left(F[T;V_1,N_1]+F[T;V-V_1,N-N_1]\right)=0 $$ と、 $$ {\partial\over\partial N_1}\left(F[T;V_1,N_1]+F[T;V-V_1,N-N_1]\right)=0 $$ を解けばよい。この二つの条件は${\partial F\over\partial V}=-P$と${\partial F\over\partial N}=\mu$が等しいという条件になるから、圧力と化学ポテンシャルが等しくなるところがつりあい点になると結論できる。

　なお、一般に微分が0というだけでは最小点とは限らず、最大点であったり極小ではあっても局所的最小であるという可能性もある。しかし今$F$は「下に凸」とわかっているので、そんなことはない（教科書には厳密な証明があるので気になる人は参照しよう）。

　$F$が$V$の関数として下に凸ということは、（微分ができる領域においては）${\partial^2 F[T;V,N]\over\partial V^2}\gt 0$ということである。これはつまり、$-{\partial P(T;V,N)\over\partial V}\gt0$つまり$P$が$V$の減少関数であることを意味する。

　${\partial P\over \partial V}\lt 0$（つまりは$F$の凸性）は、確かにつりあいが安定な条件になっている。今ある系の状態を二つに（仮想的にでいいから）分割してみる。当然このとき左右の領域の圧力は等しい（元々同じものを二つに分割したから当然だとも言えるし、そうでなくてはつりあいが保てない、とも言える）。

　左の領域が（なにかのはずみで）膨張したとしよう（右の領域はそれに応じて少し収縮する）。もし${\partial P\over \partial V}\gt0$なら、左の領域の圧力は増え、右の領域の圧力が減る。

　こうなると平衡が破れてしまって、どんどん左の領域が拡大してしまう。

変分原理 ファンデルワールスの状態方程式と相転移

ファンデルワールスの状態方程式と相転移

ファンデルワールスの状態方程式

ファンデルワールスが提唱した状態方程式は $$ \left(P+{aN^2\over V^2}\right)(V-b)=NRT $$ というもの。

　この式で$b$はある意味「最小の体積」を意味する（$V\leq b$は有り得ない）。物理的には「気体分子に大きさがあって、$b$よりも圧縮できない」という状況を示していると思えばよい。

　$a$の方は分子どうしの引力の強さを表現している数で、引力が強いと引き合う分だけ外に押す力が減ると思えばよい。

　これから$P$を求めると $$ P={NRT\over V-b}-{aN^2\over V^2} $$ となる。

　$V\ge b$の範囲で考えると、第１項の${NRT\over V-b}$は正の値を持つ$V$の減少関数、第２項の$-{aN^2\over V^2}$は負の値を持つ$V$の増加関数（ただし、$V$が大きくなるに従って第１項よりも早く0に近づく）。

　ここで、 $$ {\partial P\over \partial V}=-{NRT\over (V-b)^2}+{2aN^2\over V^3} $$ となり、状況により（具体的には${NRT\over (V-b)^2}\gt {2aN^2\over V^3}$のとき）マイナスになることに注意。当然そんなことは有り得ない。

ファンデルワールスの状態方程式は、高温では理想気体の状態方程式とほぼ同じようになる。しかし、ある程度より温度が下がると、下のようなおかしなグラフになる。

　グラフには${\partial P\over \partial V}\gt0$の領域が現れるが、現実にはこんな状況は起きないのは先に説明した通りである。

　このような状況がもし実現してしまうと、$F$が下に凸でなくなり、

のようになる。このような場合、系は（少し前に説明したように）二つの相に別れることを選ぶ（その方が$F$を小さくできる）。

　この図の赤線の$F$は実現しない部分を含むので「擬似的自由エネルギー」である）。擬似的自由エネルギーをほんとうの自由エネルギーにするには、共通接線になる線を引く（図にA,Bと示した点が共通接線の接点）。AからBまでの間では、系は状態Aと状態Bの混合状態（$\lambda:1-\lambda$に内分した点）になった方が$F$が小さい。

　共通接線ということは、傾きが等しいから、A点とB点では${\partial F\over\partial V}=-P$が等しい（圧力は同じ）。

　つまりAからBまでの体積変化の間、圧力は変化せずに体積が増加し続ける、ということになる。この直線上の状態は、Aで表現される状態とBで表現される状態の状態が（$\lambda:1-\lambda$などの比率で共存した状態である（体積を大きくするほど、Bの比率が増える）。

　これは水と水蒸気のような液相と気相が共存している状態をしめしているのである。つまり、いっけん不安定に見える（下に凸でない$F$）は、相転移の存在を示している。

　A点とB点のヘルムホルツ自由エネルギーの差は、赤線（曲線）に沿って計算しても黒線（直線）に沿って計算しても同じである（出発点と到着点が同じなのだから当然だ）。

　この条件は「系が（仮想的に）行なう仕事が等しい」ということになるから、$V$-$P$グラフの方で考えると、ABの下の面積が（直線で考えても曲線で考えても）等しい、という形になるので「Maxwellの等面積則」と呼ばれる。

熱力学関数の凸性 受講者の感想・コメント

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

エントロピーの性質