青字は受講者からの声、赤字は前野よりの返答です。
また新しいエネルギーが出てきたのでどんなときに重要となるのかなど考えておきます。
使い分けていきましょう。
エントロピーとエンタルピー。急に双子みたいな要素が出てきて焦ったがそこまで関係性はなかった。エンタルピーの方が日々気がかわいい。
実は名前ほどには似てない。
エンタルピーは初めて聞いたが、今日の説明でよく分かった。次の授業の内容も楽しみです。
うまく使うと便利な概念です。
ルジャンドル変換でエンタルピーが出せた。
ルジャンドル変換の威力を知ってください。
エンタルピーの導出ができた。実験で相転移の実験をしたが、そこで学んだ部分と今日の授業で学んだ所と合致して、頭の整理ができた。
実験で測った現象とつなげて、理解しておきましょう。
今回の内容はちゃんと整理しておこうと思った。そして、過去に学んだことが多く必要だったので復習が必要だと感じた。
過去とのつながりが大事です。
ルジャンドル変換をすることで状況によって意味がある変数に変えることで有用さを実感できた。
役に立ちます、ルジャンドル変換。
今回の授業ではエンタルピーとはどういうものかを学んだ。等圧状態でのエネルギーをエンタルピーとした。ルジャンドル変換によって、内部エネルギーから導き出せた。
つながりを理解しておきましょう。
内容をちゃんと理解できたと思います。
それはめでたい。
ルジャンドル変換についてもっと勉強しようと思った。
勉強しましょう、役に立ちます。
ルジャンドル変換とエネルギーについておさえなおしたい。
物理的意味も含めて、おさえておきましょう。
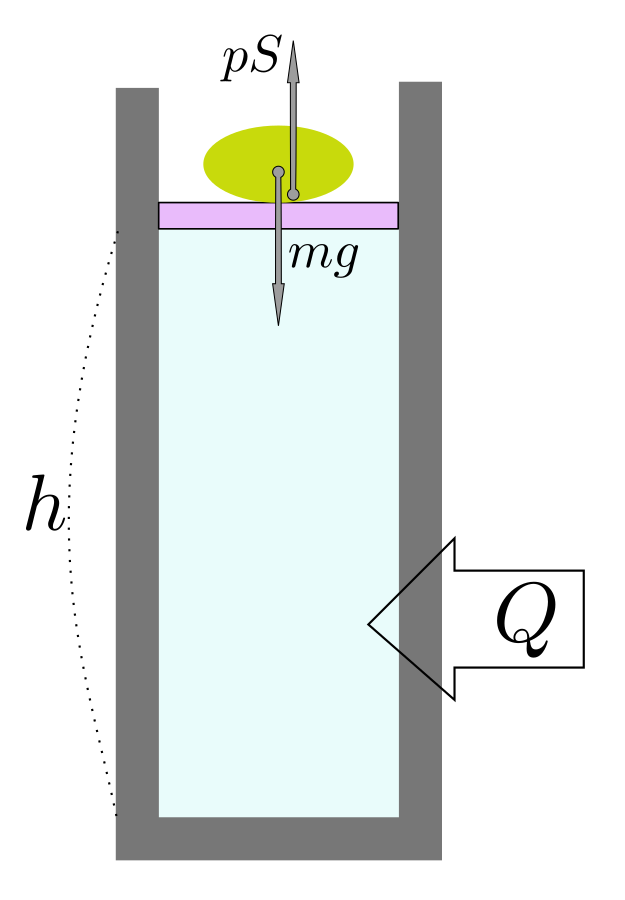
相転移→二つの状態が共存で圧力が変化しない→等圧でのエネルギーを定義した。
いろいろ話しましたが、まとめておいてください。
エンタルピーやギッブスの自由エネルギーについて分かった。
どっちも大事です。
台風12号がそろそろ来るそうですね。メガネが飛ばされないように気をつけてください。
気をつけましょう。
ルジャンドル変換の強力さをあらためて感じた。
使える計算でしょ。
聞いたことがある「エンタルピー」がでてきた。エントロピーとは似てない物理的意味だと思った。
ええ、似ているのは名前だけで、次元すら違います。
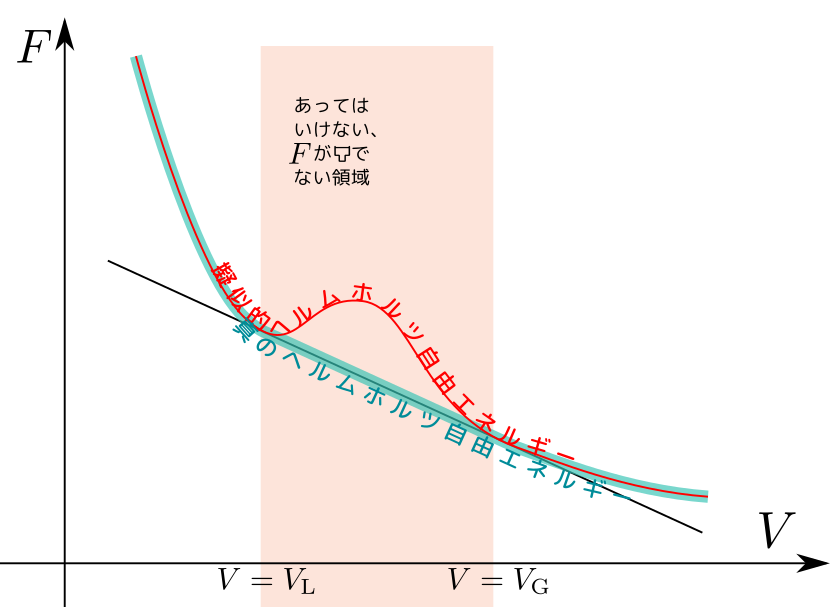
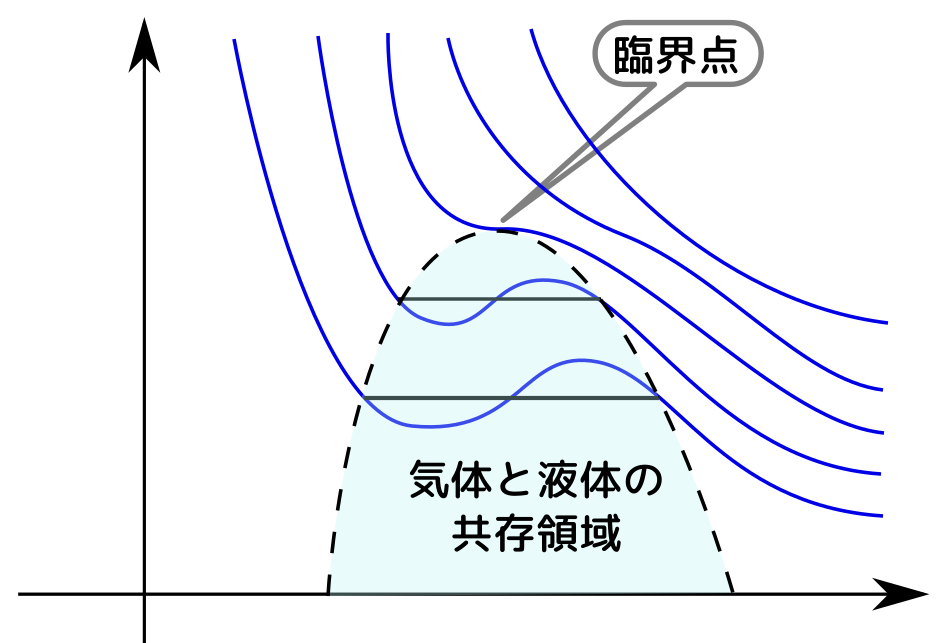
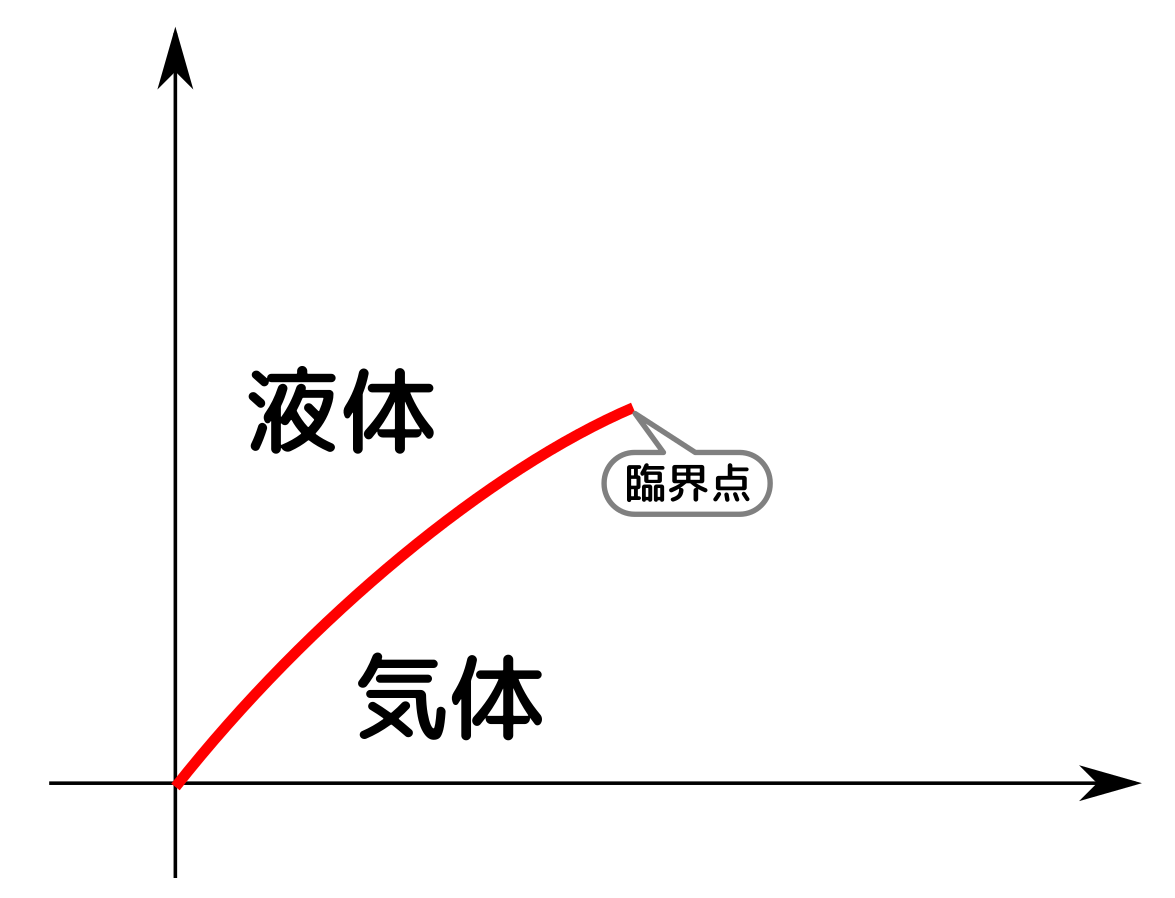
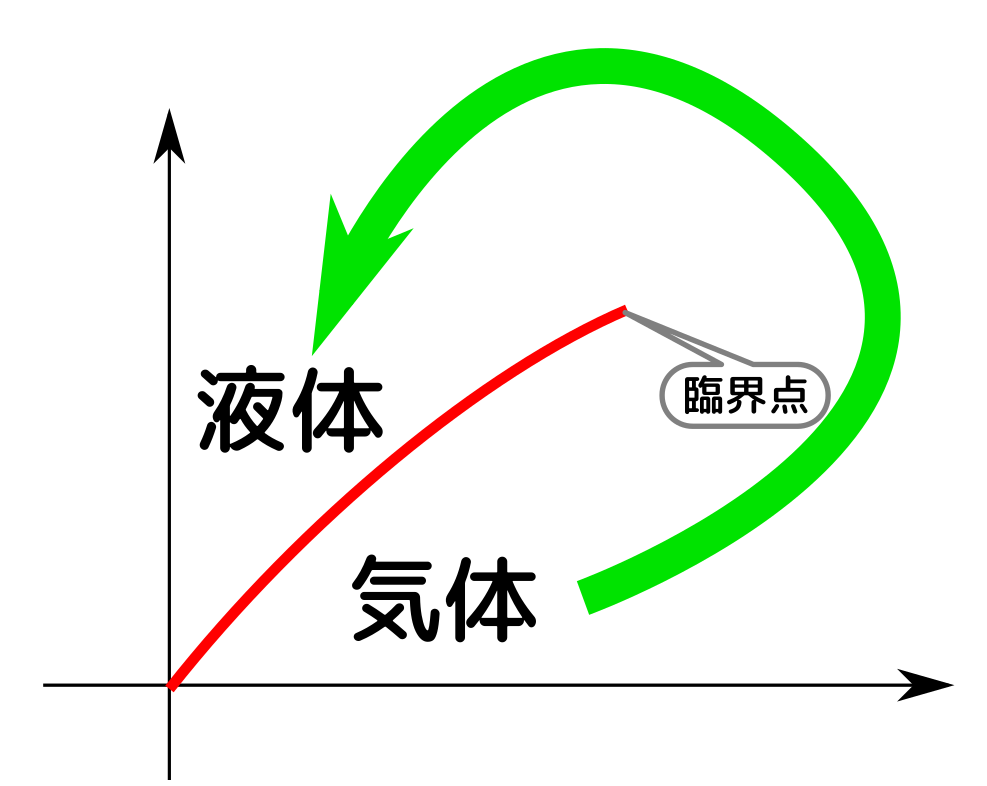
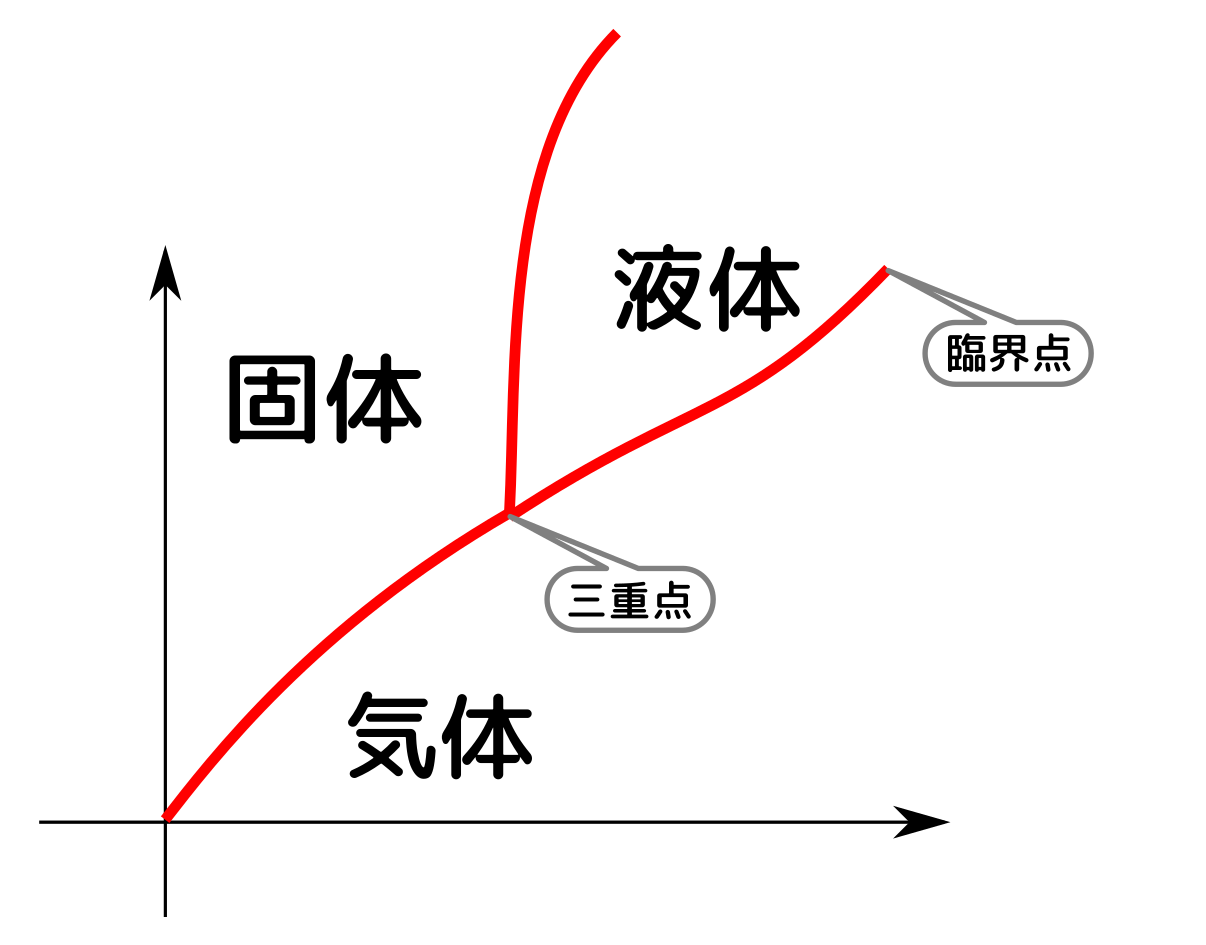
臨界点、三重点の話は興味深かった。$U,F,H$の関係性をわかったとき感動した。7/3で学習したルジャンドル変換すごい!
ルジャンドル変換は役に立つでしょ。
とうとうエンタルピーが出ましたね。そして自習、四天王の最後の1人「ギッブスの自由エネルギー$G$」が登場! この四天王をうまく使えるようになりたいです。
それぞれがどういう性格のエネルギーか、を把握しておきましょう。
ルジャンドル変換便利ですね。新たなる野望楽しみです。
ギッブス自由エネルギーも使いこなしていきましょう。
台風に負けず復習します。
今度は授業つぶれなそうでよかった。
例えば三重点が身近にある状態はなんでしょうか。氷のたくさん入った0度Cの水は三重点に位置していますか?
三重点は非常にシビアに調節しないと実現しまっせん。氷と水だと三重になってませんし。
関係式が多くでてきたので、しっかり復習する。
つながりを理解しておきましょう。
化学でエンタルピーとエントロピーについて学びましたがどう違うのかわからなかったので、今回の授業で判明してよかったです。
エンタルピーとエントロピーだと、だいぶ違います(^_^;)。
断熱、等温、等圧のルジャンドル変換での関係性が少しだけわかりました。
「少しだけ」〜〜???。
エンタルピー$H=U+PV$、ギッブスの自由エネルギー$G=U-TS+PV$。
はい。
エンタルピー$H$が出てきたので、今までのと含めて確認したい。流れるように出てきた$G$も、理解できるようにする。ルジャンドル変換を確実に。
$G$に関しては、これまでの考えがわかっていれば自然に理解できるかと思います。
相図や臨界点の話が$F$からでて面白かった。ついに4つの完全な熱力学関数が出てきた。
今日はいろいろな話があってので、よく整理しておいてください。
エンタルピー$H$を導出した。何を変数にするかという視点で、熱力学関数をルジャンドル変換を用いる上で、“熱力学”が整理できた。
いろんな表現がありますが、混乱せずに本質をつかんでください。
ルジャンドル変換をしなければいけない理由がわかりずらかった。ルジャンドル変換で繋がっている感動をもう一度考えてみます。
それは前にで説明してますので見返しておいてください。
ルジャンドル変換のありがたさを知りました。
とてもありがたいもんです。
色々な変数を固定させることで、色々な実験ができることがわかった。
実験に応じて、変数の取り方を考えるわけです。
とてもよく分かりました。
それはめでたい。
ルジャンドル変換が好きになりました。
それはよいことです。
等圧の時のエネルギーもでてきたので、しっかりと整理したいと思う。
状況に応じ、使い分けてください。
エンタルピーも出てきたので、混乱しないように注意する。
まとめておきましょう。
ルジャンドル変換が重要なので、使いこなしたい。
はい、重要です。
エンタルピーはエネルギーなので、示量変数ですか。「潜熱」とは何ですか。相転移点は臨界点と同じことですか。
エンタルピーも示量変数です。潜熱は次回やりますが、今日やった「液相→気相のような相変化を起こす時に必要な熱(=エンタルピーの変化)」です。臨界点は相転移が起こる/起こらないの境目で、相転移点とは別です。
4つの熱力学関数が揃った! 次回で最後かと思うとさみしいです。
まだまだ話し足りない感じはします。