等温操作と断熱操作:もう一度整理
ここまでの復習
ここまでの流れをまとめておこう。
第1講で、「熱」とは何か?という問いから始めた。ここまで話が進んだので、「熱」とは何かも語れるようになった。
もともと、力学ではまず「仕事」を定義し、その仕事の分だけ増減する量としてエネルギーを定義する。だからエネルギーの移動形態は、まず(定義により)仕事。
エネルギーの移動形態には、「仕事」という目に見える形のもの(←こちらに音や光は入れてもいいだろう)と、目に見えない形のものがあり、ある状態のエネルギーを$U(T;X)$と書いたとき、
$U(T;X)-U(T';X')=W(T;X\to T';X')-Q(T;X\to T';Q')$
のように、エネルギーの変化(上の式の左辺)のうち、仕事($W$)という目に見える移動の他に行われているエネルギーの移動を熱($Q$)と呼ぶわけである。
断熱操作で行う仕事は内部エネルギー$U$を定義するのに使われるが、一方等温操作で行う「最大仕事」はヘルムホルツの自由エネルギーで定義される。
さて、ここまで等温操作と断熱操作を使っていろんな過程を見てきたので、これを組み合わせた過程を考えたい。そのためにまず、しばらく話を理想気体の場合に限りつつ、等温操作と断熱操作の性質を見よう。
等温操作と断熱操作
熱力学ではよく体積$V$を横軸、圧力$P$を縦軸にしたグラフ($V$-$P$グラフ)を描く。理想気体では状態方程式$PV=NRT$が成立するから、では$V$-$P$グラフ上では$PV=$一定のグラフ(反比例のグラフ)になる。
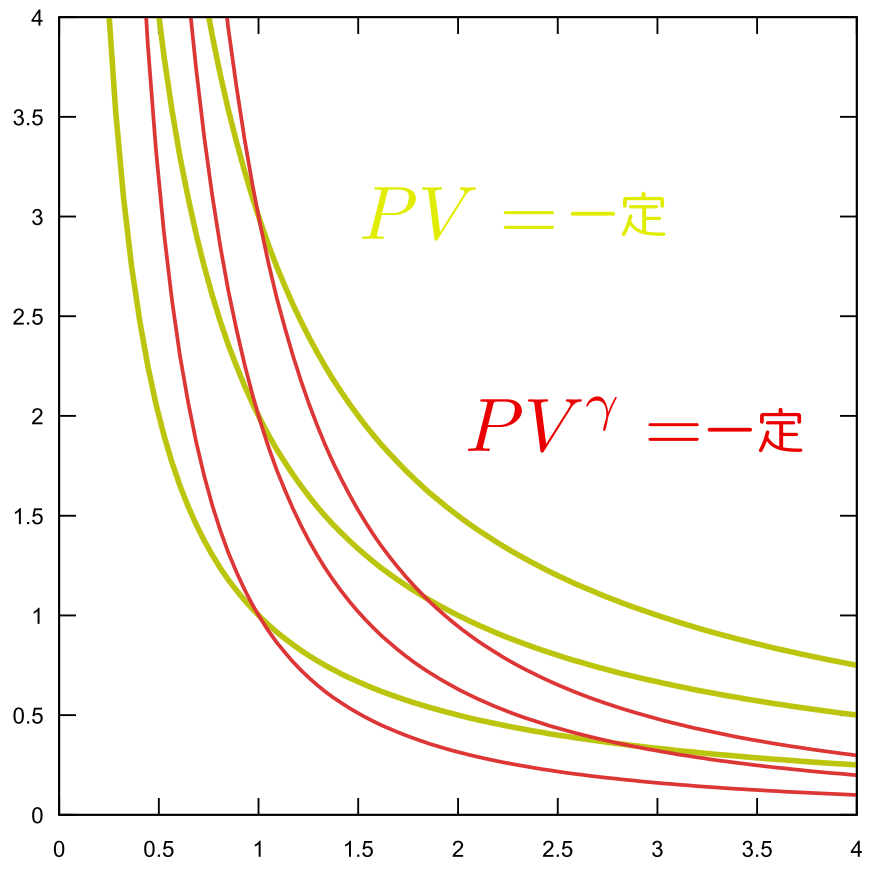
一方断熱操作では$PV^\gamma=$一定という少し違ったグラフになる(↑を参照)。
$PV^\gamma=$一定となるのは、理想気体では内部エネルギーが$U=NC_VT$と表せることから、
$NC_V \mathrm dT = -P\mathrm dV$
という微分方程式が成立する、ということからわかる。前にも同様の計算をやったのだが一応やっておくと、$T={PV\over NRT}$だから、$\mathrm dT = {\mathrm dPV+P\mathrm dV\over NR}$として整理(←このあたりの偏微分を使う計算がピンと来ない人がいくらかいたが、こういう計算には慣れよう!)することで、
${C_V\over R}\left(\mathrm dPV+P\mathrm dV\right)=-P\mathrm dV$
となり、変数分離すると
${C_V\over R}{\mathrm dP\over P}= -\left(1+{C_V\over R}\right){\mathrm dV\over V}$
となり、積分は
$\log P = -{C_V+R\over C_V}\log V + $積分定数
となって、$\gamma={C_V+R\over C_V}$とすれば、$PV^\gamma=$一定がわかる。
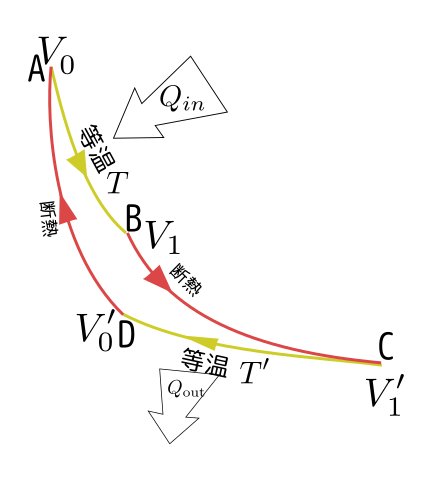
カルノーサイクル
等温操作と断熱操作を組み合わせて以下のような運動をさせる(アニメーションが次のページにある)。
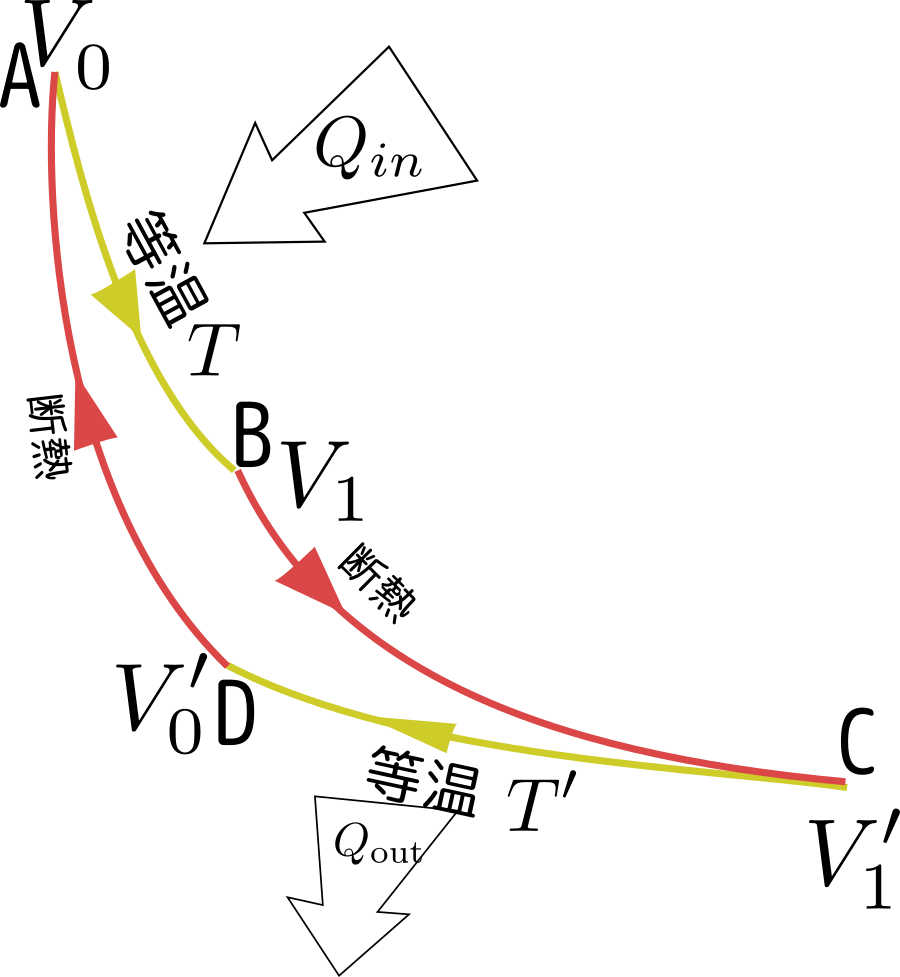
これは何をやりたいかというと、一周して元の状態に戻す間にこの気体に仕事をさせたい。図のように動くと、膨張しているときは収縮しているときに比べて圧力が高いから、全体としてプラスの仕事をしていることになる。エネルギー収支の式$\Delta U=Q-W$を考えると、一周回って元に戻るから$\Delta U=0$となり、このとき$Q=W$である。
断熱操作では熱の出入りがない。図で温度$T$の等温操作(A→B)で入ってくる熱を$Q_{\rm in}$、温度$T'$の等温操作(C→D)で出ていく熱を$Q_{\rm out}$とすると、全体で熱は$Q_{\rm in}-Q_{\rm out}$入ってきたことになり、これが仕事になるから、$Q_{\rm in}-Q_{\rm out}=W$である。ガソリンで動く車のエンジンであれば、$Q_{\rm in}$はガソリンによって生まれる熱量であり、それを(車のラジエータなど)で冷やす過程がC→Dである。