今日の講義の内容
変分原理
ここで扱う「変分原理」というのは、初等力学の頃からよく出てきた物事はエネルギーが低い方へと進むということを数式で表現したものになる。
熱力学でも$U$や$F$などのエネルギーを最小化する方向へ変化が起こるという考え方で物理現象を予言しよう、というのが変分原理である。
平衡状態にある二つの系$(T;V_1,N_1)$と$(T;V_2,N_2)$を接触させて壁を取り除いてしばらく待つと、$(T,\underbrace{V_1+V_2}_V,\underbrace{N_1+N_2}_N)$という平衡状態に達する（温度は最初から同じであったことに注意）。
このとき、ヘルムホルツの自由エネルギーの差
$$ F[T;V_1,N_1]+F[T;V_2,N_2]-F[T;V,N] $$を考えると、これはこの変化を行った時の最大仕事である。しかし最大仕事が行われるのは準静的な操作の時で、単に壁を取り除くという操作は準静的ではないからその時の仕事は最大仕事ではない。壁を取り除いただけでは何も動かしたりしないから、仕事は0である。最大仕事は0よりは大きいことだけはわかるから、
$$ F[T;V_1,N_1]+F[T;V_2,N_2]-F[T;V,N]\geq 0 $$という不等式を満たす。つまり
$$ F[T;V_1,N_1]+F[T;V_2,N_2]\geq F[T;V,N] $$で、「壁を取り払って（たとえば）気体を混ぜてしまうと、ヘルムホルツ自由エネルギーは減る（か変化しない）」ということがわかる。
二つの系が物質量$N$のやりとりができる状況にしてみよう（具体的には、壁に穴を開けて空気分子などが行き来できるようにする）。すると、最初$N_1,N_2$だった物質量が、$\tilde N_1,\tilde N_2$（もちろん、$N_1+N_2=\tilde N_1+\tilde N_2=N$）になったところで平衡に達したとしよう。この時もヘルムホルツ自由エネルギーは減る（か、変化しない）はずで、逆に言えば「もう減らせない」というところで変化が止まるはず、と考えると、
$$ F[T;V_1,\tilde N_1]+F[T;V_2,\tilde N_2]=\min_{N_1,N_2\atop N_1+N_2=N}F[T;V_1,N_1]+F[T;V_2,N_2] $$が成立するだろう（最小値が一個じゃない場合については後で考える）。
体積がやりとりされる（間の壁が押されて動くような状況）についても同様に、
$$ F[T;\tilde V_1,N_1]+F[T;\tilde V_2,N_2]=\min_{V_1,V_2\atop V_1+V_2=V}F[T;V_1,N_1]+F[T;V_2,N_2] $$が成立する。
ヘルムホルツの自由エネルギーの凸性
以上のように「二つの系を合体させると$F$は減るはず」という原理から、$F$という関数は、 $$ F[T;\lambda V_1+(1-\lambda)V_2,\lambda N_1+(1-\lambda)N_2]\leq \lambda F[T;V_1,N_1]+(1-\lambda) F[T;V_2,N_2] $$
という不等式を満たす。$(T;\lambda V_1+(1-\lambda)V_2,\lambda N_1+(1-\lambda)N_2)$とは、$(T;V_1,N_1)$と$(T;V_2,N_2)$を$\lambda:1-\lambda$に内分した点である。単純な例として$\lambda={1\over2}$の場合を考えればこれは $$ F[T;{V_1+V_2\over2},{N_1+N_2\over 2}]\leq {F[T;V_1,N_1]+F[T;V_2,N_2]\over2} $$ で、「中点での$F$は両端の平均より小さい」ということを意味している。
$F$が二階微分可能である場合、凸性は${\partial^2 F\over\partial V^2}>0$を意味する。
つりあい点
最小になる点を探すには「微分して0」を解けばよい。すなわち、 $$ {\partial\over\partial V_1}\left(F[T;V_1,N_1]+F[T;V-V_1,N-N_1]\right)=0 $$ と、 $$ {\partial\over\partial N_1}\left(F[T;V_1,N_1]+F[T;V-V_1,N-N_1]\right)=0 $$ を解けばよい。この二つの条件は${\partial F\over\partial V}=-P$と${\partial F\over\partial N}=\mu$が等しいという条件になるから、圧力と化学ポテンシャルが等しくなるところがつりあい点になると結論できる。
なお、一般に微分が0というだけでは最小点とは限らず、最大点であったり極小ではあっても局所的最小であるという可能性もある。しかし今$F$は「下に凸」とわかっているので、そんなことはない（教科書には厳密な証明があるので気になる人は参照しよう）。
$F$が$V$の関数として下に凸ということは、（微分ができる領域においては）${\partial^2 F[T;V,N]\over\partial V^2}\gt 0$ということである。これはつまり、$-{\partial P(T;V,N)\over\partial V}\gt0$つまり$P$が$V$の減少関数であることを意味する。
${\partial P\over \partial V}\lt 0$（つまりは$F$の凸性）は、確かにつりあいが安定な条件になっている。今ある系の状態を二つに（仮想的にでいいから）分割してみる。当然このとき左右の領域の圧力は等しい（元々同じものを二つに分割したから当然だとも言えるし、そうでなくてはつりあいが保てない、とも言える）。
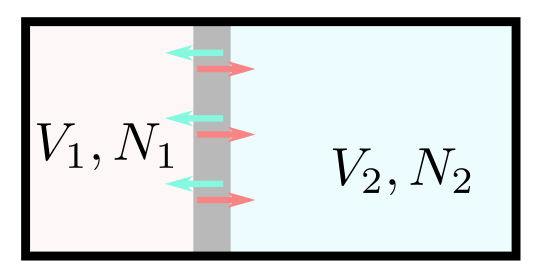
左の領域が（なにかのはずみで）膨張したとしよう（右の領域はそれに応じて少し収縮する）。もし${\partial P\over \partial V}\gt0$なら、左の領域の圧力は増え、右の領域の圧力が減る。
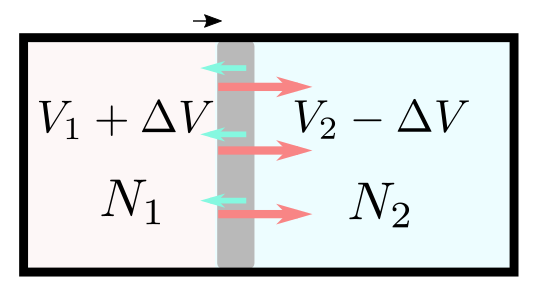
こうなると平衡が破れてしまって、どんどん左の領域が拡大してしまう。
ヘルムホルツ自由エネルギーが「下に凸（
）」でなかったらどういうおかしいことが起こるかを一つの例で示そう。
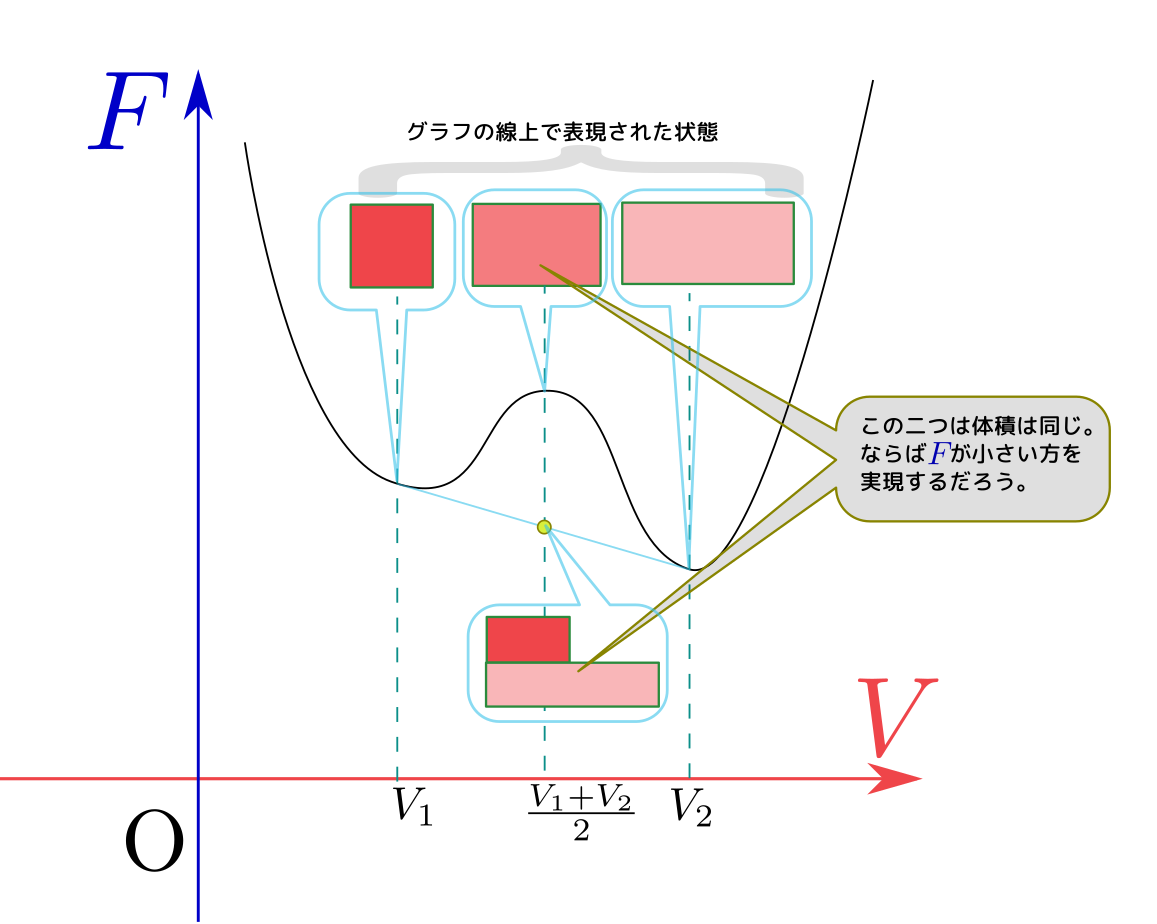
上のような「下に凸でない」$F$が存在したとしよう。すると明らかに、$F[T,{V_1+V_2\over2}]$より、$F[T,V_1]+F[T,V_2]\over2$の方が小さい。
つまり同じ${V_1+V_2\over2}$という体積を占める状態であれば、${V_1\over2},{V_2\over2}$という体積を持った二つの状態に別れた方が、ヘルムホルツ自由エネルギーが小さくなる（この例は中点で見せたが、$\lambda:1-\lambda$で内分した点でも同様のことが言える）。
このような場合、実際に起こるのは↓のような変化過程であろう。
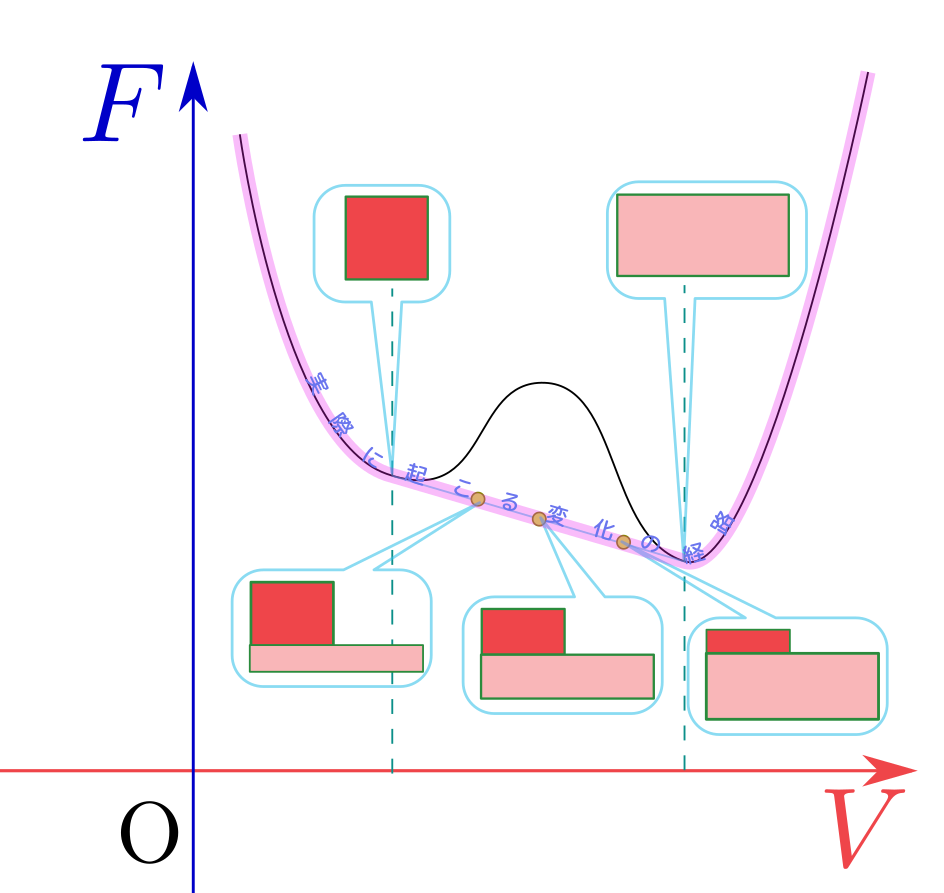
実はこれが「液体」→「気体」などの「相転移」の起こる過程である。
図にあるように中間点では密度の濃い部分
と密度の薄い部分
が共存する。それが液相（液体の状態）と気相（気体の状態）なのである。
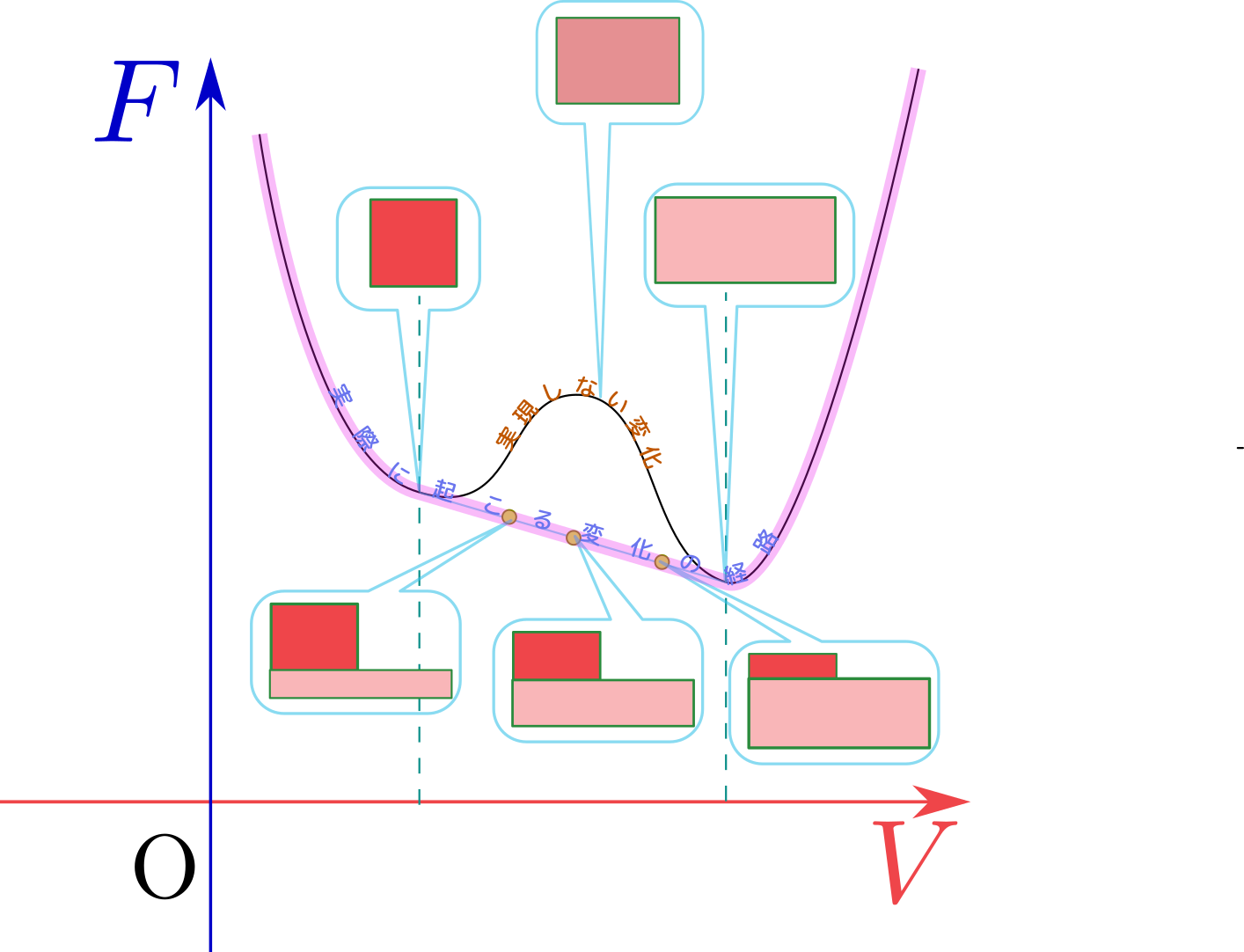
上にあるような中間色の状態で、密度が一様になった状態
は、密度が一様でない、二つの相に分かれた状態よりエネルギーが高いから、存在できない（存在したとしてもすぐによりエネルギーの低い状態へと変化してしまう）、というわけ。