今日の講義の内容
まず復習として、下の図のようなカルノーサイクルが動いたとき、それぞれの過程での「系のした仕事」「系が吸収する熱」についての表を作ってみよう、という課題を出した。
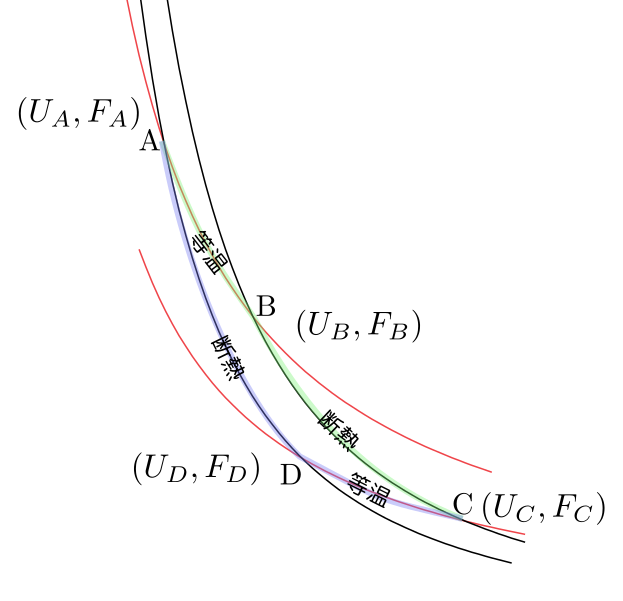
図に書いた$(U_*,F_*)$はそれぞれの状態での内部エネルギーとヘルムホルツ自由エネルギーである。
| 系のした仕事 | 系が吸収した熱 | |
| A→B(等温準静的操作) | ||
| B→C(断熱準静的操作) | ||
| C→D(等温準静的操作) | ||
| D→A(断熱準静的操作) |
これだけではなかなか手が動かないようなので、いくつかヒントを出した。
第1ヒントを見たい人は左の三角をクリック。
まず、表に「内部エネルギーの変化」を加えて、
| 系のした仕事 | 系が吸収した熱 | 内部エネルギーの変化 | |
| A→B(等温準静的操作) | |||
| B→C(断熱準静的操作) | |||
| C→D(等温準静的操作) | |||
| D→A(断熱準静的操作) |
とする。熱力学第1法則から、
(内部エネルギーの変化)=(吸収した熱)ー(した仕事)
が成立することに注意すればよい。
第1ヒントを取り入れた結果を見たい人は左の三角をクリック
それぞれの状態の内部エネルギーは与えられているので、まず内部エネルギーの変化のところが、
| 系のした仕事 | 系が吸収した熱 | 内部エネルギーの変化 | |
| A→B(等温準静的操作) | $U_B-U_A$ | ||
| B→C(断熱準静的操作) | $U_C-U_B$ | ||
| C→D(等温準静的操作) | $U_D-U_C$ | ||
| D→A(断熱準静的操作) | $U_A-U_D$ |
のように埋まる。
第2ヒントとそれを取り入れた結果をみたい人は左の三角をクリック
断熱操作では吸収した熱は0にきまっているから、
| 系のした仕事 | 系が吸収した熱 | 内部エネルギーの変化 | |
| A→B(等温準静的操作) | $U_B-U_A$ | ||
| B→C(断熱準静的操作) | 0 | $U_C-U_B$ | |
| C→D(等温準静的操作) | $U_D-U_C$ | ||
| D→A(断熱準静的操作) | 0 | $U_A-U_D$ |
である。
第3ヒントを見たい人は左の三角をクリック。
ヘルムホルツ自由エネルギーと内部エネルギーの定義の仕方を思い出すと、
ヘルムホルツ自由エネルギーの定義
等温準静操作において、($F$の変化)=ー(した仕事)である。あるいは、 $$ W=F_{前}-F_{後} $$ が成立する。
内部エネルギーの定義
断熱操作において、($U$の変化)=ー(した仕事)である。あるいは、 $$ W=U_{前}-U_{後} $$ が成立する。
である。
さらに第4ヒントとその結果を見たい人は以下をクリック
さらに$F$と$U$の定義から、
| 系のした仕事 | 系が吸収した熱 | 内部エネルギーの変化 | |
| A→B(等温準静的操作) | $F_A-F_B$ | $U_B-U_A$ | |
| B→C(断熱準静的操作) | $U_B-U_C$ | 0 | $U_C-U_B$ |
| C→D(等温準静的操作) | $F_C-F_D$ | $U_D-U_C$ | |
| D→A(断熱準静的操作) | $U_A-U_D$ | 0 | $U_A-U_D$ |
最終結果を見たい人は左の三角をクリック
さらに熱力学第1法則から、
| 系のした仕事 | 系が吸収した熱 | 内部エネルギーの変化 | |
| A→B(等温準静的操作) | $F_A-F_B$ | $U_B-U_A+F_A-F_B$ | $U_B-U_A$ |
| B→C(断熱準静的操作) | $U_B-U_C$ | 0 | $U_C-U_B$ |
| C→D(等温準静的操作) | $F_C-F_D$ | $U_D-U_C+F_C-F_D$ | $U_D-U_C$ |
| D→A(断熱準静的操作) | $U_A-U_D$ | 0 | $U_A-U_D$ |
これで系が吸収する熱が得られた。この結果から、 $$ Q_{\rm in}=U_B-U_A+F_A-F_B $$ と $$ Q_{\rm out}=-(U_D-U_C+F_C-F_D) $$ となる($Q_{\rm out}$の方は符号をひっくり返さなくてはいけないことに注意)。
Kelvinの原理は、 $$ {U_B-U_A+F_A-F_B\over T_{\rm in}}={-(U_D-U_C+F_C-F_D)\over T_{\rm out}} $$ である。少し整理すると、 $$ {U_B-F_B\over T_{\rm in}}-{U_A-F_A\over T_{\rm in}}={U_C-F_C\over T_{\rm out}}-{U_D-F_D\over T_{\rm out}} $$ または、 $$ {U_B-F_B\over T_{\rm in}} -{U_C-F_C\over T_{\rm out}} ={U_A-F_A\over T_{\rm in}} -{U_D-F_D\over T_{\rm out}} $$ と書くことができる。上の式は(Bでの状態量)ー(Aでの状態量)=(Cでの状態量)ー(Dでの状態量)という式で、下の式は(Bでの状態量)ー(Cでの状態量)=(Aでの状態量)ー(Dでの状態量)という形になっていることに注意。
ここから後は、(リンク先とは記号が少し異なっているが、中身は同じである)のアニメーションを見て、その後のエントロピーの説明までを今回は話した。