今日の講義の内容
復習
最初にもう一度、ここまでのまとめ。エントロピーの定義まで考えた後で、内部エネルギー$U$とヘルムホルツ自由エネルギーの定義についてまとめよう。
| 定義 | 微小変化 | |
| $U$ | 「断熱(こちらには「準静的」は入らない)操作でした仕事の分減るエネルギー」 | $\mathrm dU=T\mathrm dS-P\mathrm dV$(断熱なら第1項は消える) | $F$ | 「等温準静的作でした仕事の分減るエネルギー」 | $\mathrm dF=\fbox{?}\mathrm dT-P\mathrm dV$(等温なら第1項は消える) |
さて、この$\fbox{?}$については後で考えよう。
Clausius流の視点
等温操作において、熱が$\Delta Q$だけ流入するときに $$ \Delta S={\Delta Q\over T} $$ のようにエントロピーが変化する、というのがClausius流のエントロピーの定義である。一般の操作においては、それを微小な等温操作と微小な断熱操作の繰り返しと考えて $$ \Delta S=\int {\mathrm dQ\over T} $$ のように極限では積分になると考える。
この考え方においてはエントロピー増大則は以下に述べるように「熱は高温から低温に流れる」という法則になる(熱力学第2法則はKelvinの原理やPlanckの原理として出てきたが、三つめの表現としてこれがある)。
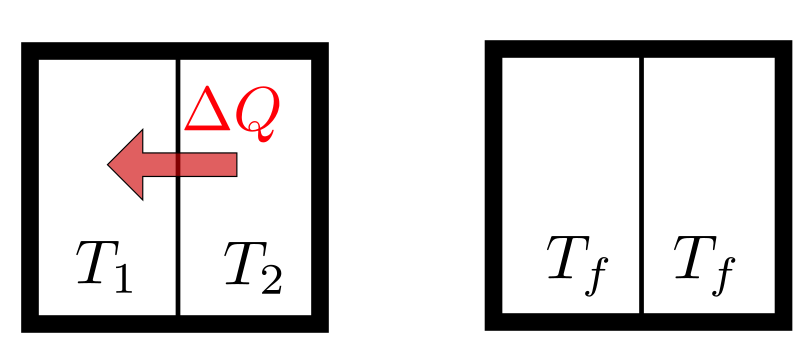
上の図のように、温度$T_1$の系と温度$T_2$の系($T_1 < T_2$)が接触し、熱の移動により最終的に温度$T_f$になったところで平衡に達したとしよう。
微小な(まだ温度が変化しない程度の)熱移動を考えると、そのとき左の系のエントロピーは${\Delta Q\over T_1}$だけ増加する。一方右の系は$\Delta Q$の熱が出て行ったから、エントロピーが${\Delta Q\over T_2}$だけ減少する。結果として全系のエントロピーは $$ {\Delta Q\over T_1}-{\Delta Q\over T_2}=\Delta Q\left({1\over T_1}-{1\over T_2}\right) $$ だけ増加する($T_1 < T_2$だから、この式は正である)。
つまり、「エントロピーは増大する」ということは「熱が高温から低温へ移動する」というある意味「あたりまえ」のこと(経験則)を表現していることになる。
こう考えると、温度差があると平均化されてしまう、というのがエントロピー増大則だ、とも言える。宇宙全体がエントロピー増大則をそのまま適用して考えると、最後は宇宙の全てが等温、等質になって、面白いことが何も起きなくなる(宇宙の熱死)。
複合系のエントロピー
系が$(T;X)\to(T';X')$のように変化するときに断熱操作ならエントロピーは減らない、ということはここまででみた。では系がいろんな温度の系の集合(複合系)であった場合にもエントロピーは減らないのだろうか、ということを考えておく。
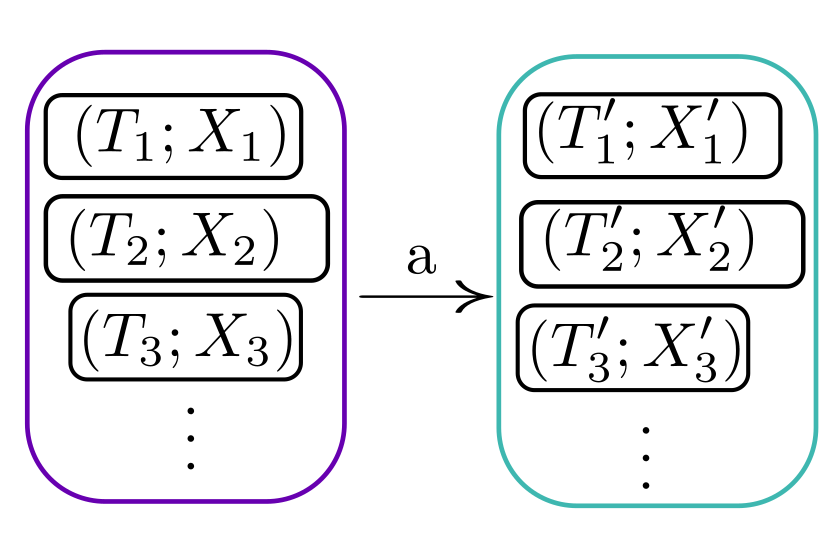
図のような複合系の変化が断熱変化で起こりえるかどうかは、 $$ S(T_1;X_1)+S(T_2;X_2)+S(T_3;X_3)+\cdots $$ と $$ S(T'_1;X'_1)+S(T'_2;X'_2)+S(T'_3;X'_3)+\cdots $$ の大小を比較すれば(大きくなっているなら可能、小さくなっているなら不可能と)わかるだろうか?
それを判断するには、それぞれの状態から断熱準静操作だけを使って温度を調整した、以下のような状態を考える。
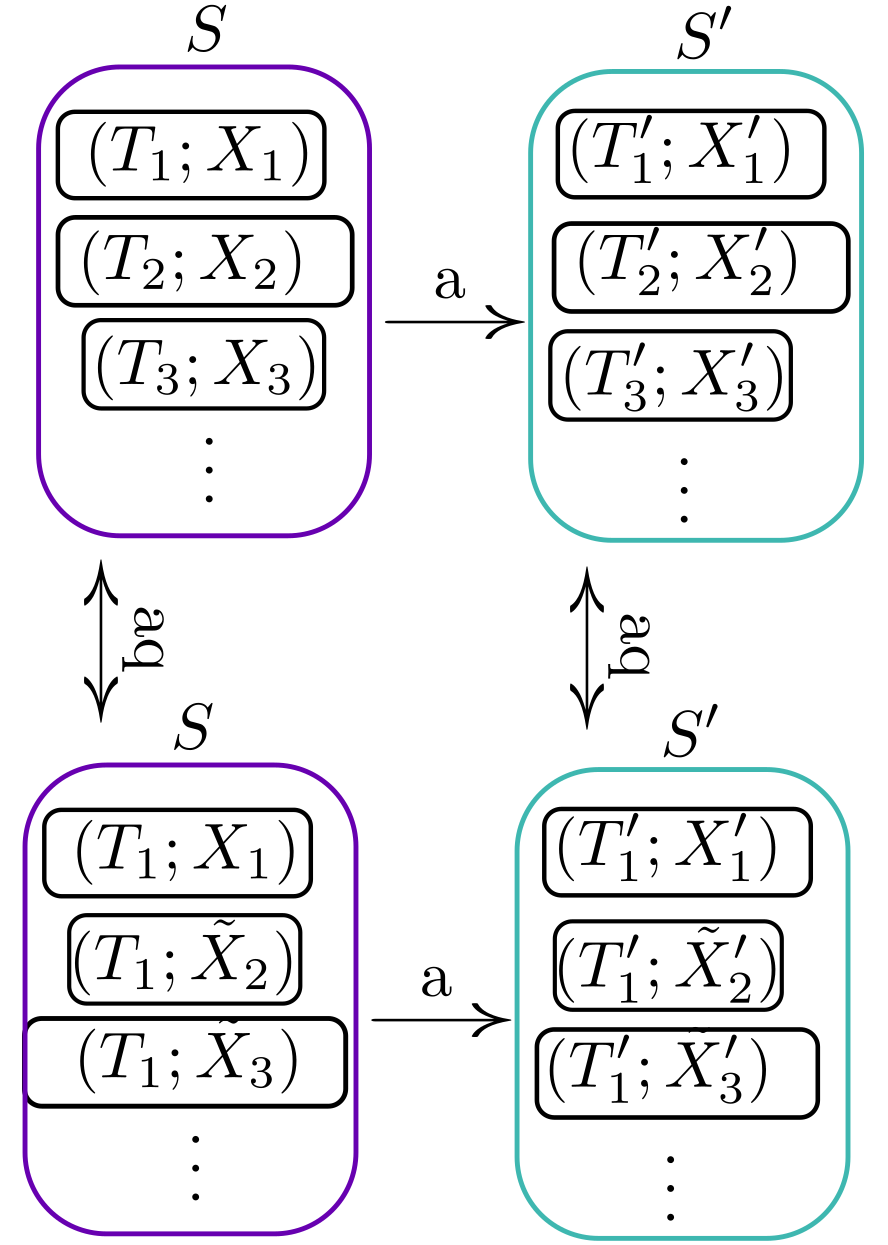
上の段と下の段は断熱準静的操作でつながっているので、エントロピーは変化していない。そして、下の段は温度は均一なので、 $S$と$S'$を比較して$S < S'$なら可能な操作だと結論できる。こうして、上の段に関してもエントロピーの大小で可能な操作かどうかが判断できる。
ヘルムホルツ自由エネルギーの微分
ヘルムホルツの自由エネルギー$F[T;V,N]=U(T;V,N)-TS(T;V,N)$を$T$で微分してみる。
$$ {\partial F[T;V,N]\over\partial T}={\partial U(T,V,N)\over\partial T}-S(T;V,N)-T{\partial S(T;V,N)\over \partial T} $$となる。
すでに示したように、${\partial U(T,V,N)\over\partial T}=T{\partial S(T;V,N)\over \partial T}$だから、
$$ {\partial F[T;V,N]\over\partial T}=-S(T;V,N) $$である。つまり、$F$を$T$で微分すると$S$が求められる。
具体的に$S$の定義式を微分して確認しよう。独立変数を$S,V$にすることにして、 $$ S={U(S,V)-F(T(S,V),V)\over T(S,V)} $$ と書く。ここで$S,V$を決めると$T$は決まるから$T(S,V)$のように書いた(つまり$T$は従属変数であって独立変数ではない)。
我々の考えたいのは断熱操作だから$S$を一定にして$V$で微分する(断熱して膨張させるということだ)。
「$S$を一定にして」の微分だから左辺は0となり、 $$ 0={\left({\partial U(S,V)\over\partial V}\right)_S-\left({\partial F(T,V)\over\partial T}\right)_V\left({\partial T(S,V)\over\partial V}\right)_S-\left({\partial F(T,V)\over\partial V}\right)_T\over T(S,V)}-{U-F\over T^2}\left({\partial T(S,V)\over\partial V}\right)_S $$ となる。$F(T(S,V),V)$を微分するとき、$V$が2箇所にあることと、最初にある$V$を微分するときは合成関数の微分になるので「$F$を$T$で微分して、さらに$T$を$V$で微分したものを掛ける」という計算になることに注意。
ここで、$\left({\partial U(S,V)\over\partial V}\right)_S$と$\left({\partial F(T,V)\over\partial V}\right)_T$はどちらも$-P$だから消せて、 $$ 0={-\left({\partial F(T,V)\over\partial T}\right)_V\left({\partial T(S,V)\over\partial V}\right)_S\over T(S,V)}-{U-F\over T^2}\left({\partial T(S,V)\over\partial V}\right)_S $$ となり、これを整理すれば$\left({\partial F(T,V)\over\partial T}\right)_V=-{U-F\over T}=-S$を得る。
以上、ちょっとややこしい計算をしたので、もうちょっと楽な考え方を示しておこう。 $$ \mathrm dU=T\mathrm dS-P\mathrm dV $$ と$F=U-TS$から$\mathrm dF$を求める。まず $$ \mathrm dF=\mathrm dU-\mathrm dT S - T\mathrm dS $$ である。これに$\mathrm dU=T\mathrm dS-P\mathrm dV$を代入するとあっさりと、 $$ \mathrm dF=-S\mathrm dT - p\mathrm dV $$ が出る。