今日の講義の内容

相転移

　先週の最後で相転移について簡単に紹介したので、もう少し詳しく話しておこう。

　前回も説明したことだが、状態方程式などから計算した擬似的ヘルムホルツ自由エネルギーが「下に凸」でない状況を含んでいると、接線を引いて「下に凸」になる「正しいヘルムホルツ自由エネルギー」を作ることができる。

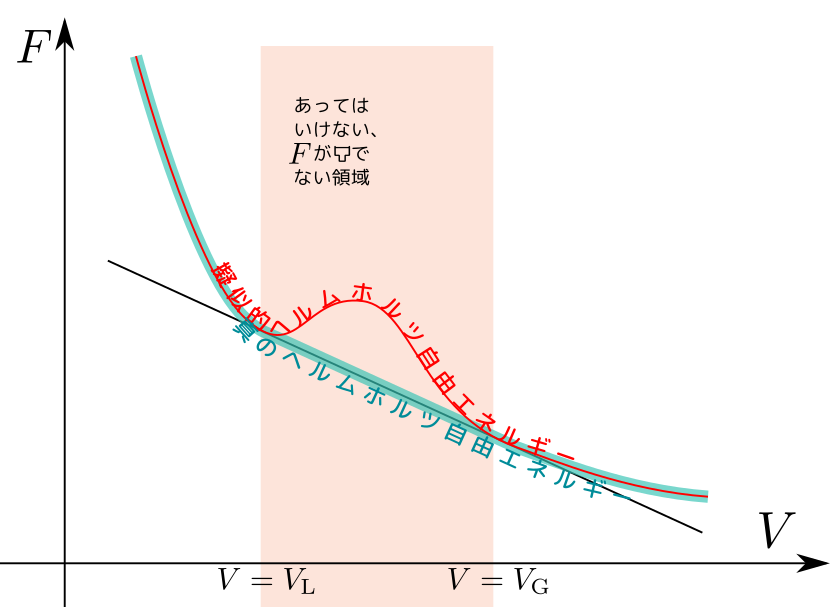
　その段階で$F$のグラフが直線になる（つまり、${\partial^2 F\over\partial V^2}=-{\partial P\over \partial V}=0$になる）状況が現れた。この状況$V_{\rm L}\leq V\leq V_{\rm G}$では異なる${N\over V}$の状況が共存し、圧力は$p=p_{\rm v}$で一定になる。この時化学ポテンシャル$\mu$も一定である（$F=-Vp+\mu N$という関係から$\mu={F+Vp\over N}$とすれば、この範囲では$F+Vp$が一定値になる）。

　上の図の赤く塗った部分では、圧力すなわち$-{\partial F\over\partial V}$が一定のままで体積が変化する。これが「気相・液相の共存領域」になる。

　この共存領域を$V$-$P$のグラフ上に表現すると↓のようになる。

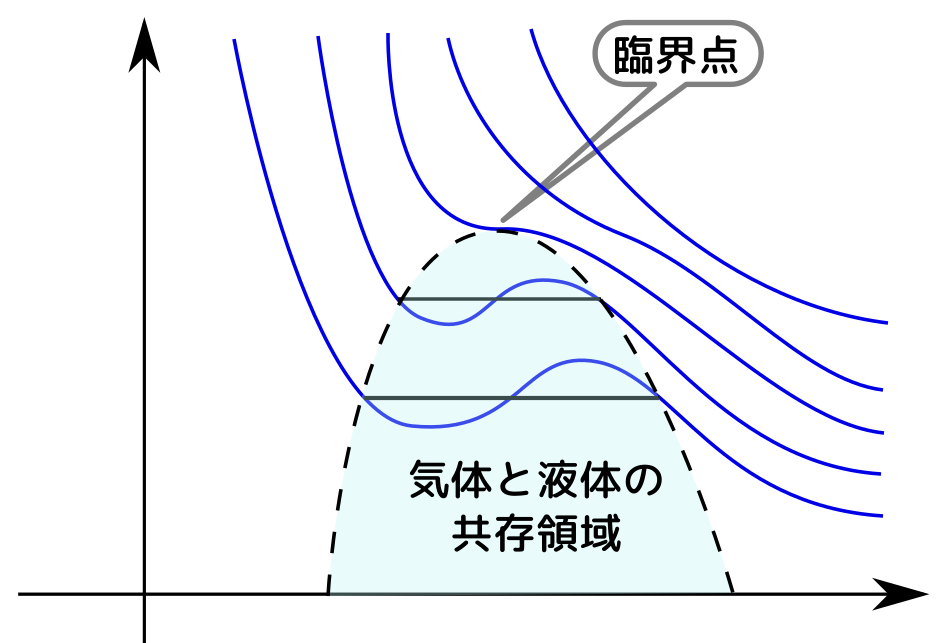
　この間に、たとえば液体→気体と相転移したなら、ぐっと体積が増える（液体窒素→気体窒素の場合で700倍）。

　温度がある程度より高いと、$V$-$P$グラフは理想気体同様の単調減少な関数になり、先に説明したような液相←→気相の変化（相転移）が起きなくなる。このときの温度を「臨界温度」と言う。

相図

　よって、気相と液相がどうなっているかを$T$-$P$のグラフ上に書くと、

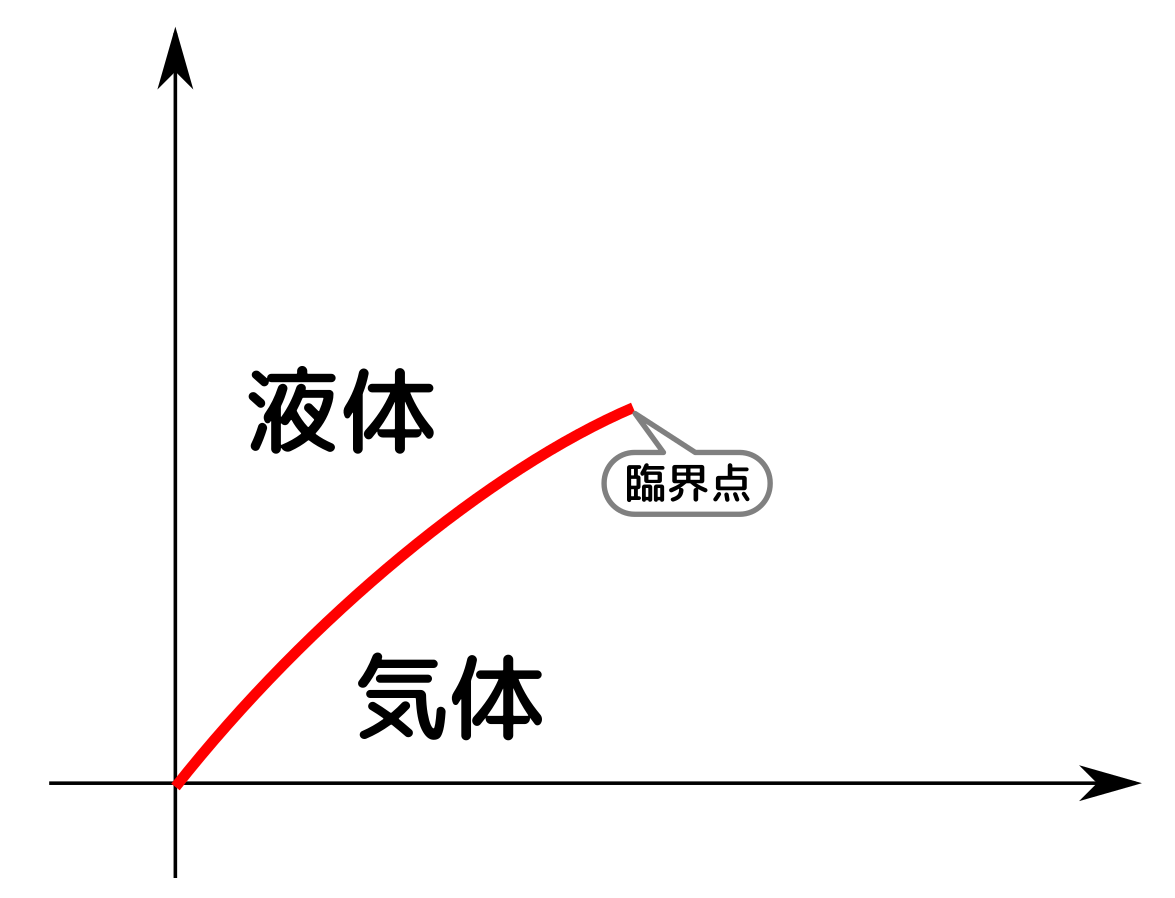
のようになる。臨界点より温度が高い状況では、液体と気体は劇的な相転移を経ることがない。むしろ、「臨界点より外では液体と気体の区別がない」という状況になる。

授業ではここで、酢酸ナトリウムの過冷却液体に衝撃を与えると「液体→固体」の相転移が起こり、同時に熱が発生することのデモンストレーション実験を見せた。

　一つ前の図の「共存領域」という面積のあった部分が、この図では直線にぺしゃっと潰れてしまっている。こっちのグラフは$T$-$P$のグラフで、共存領域では$P$が変化せずに$V$が変化して、液体←→気体と変化するのでこうなる。

　臨界点より向こうを回りこんだら、相転移せずに気体が液体になる。

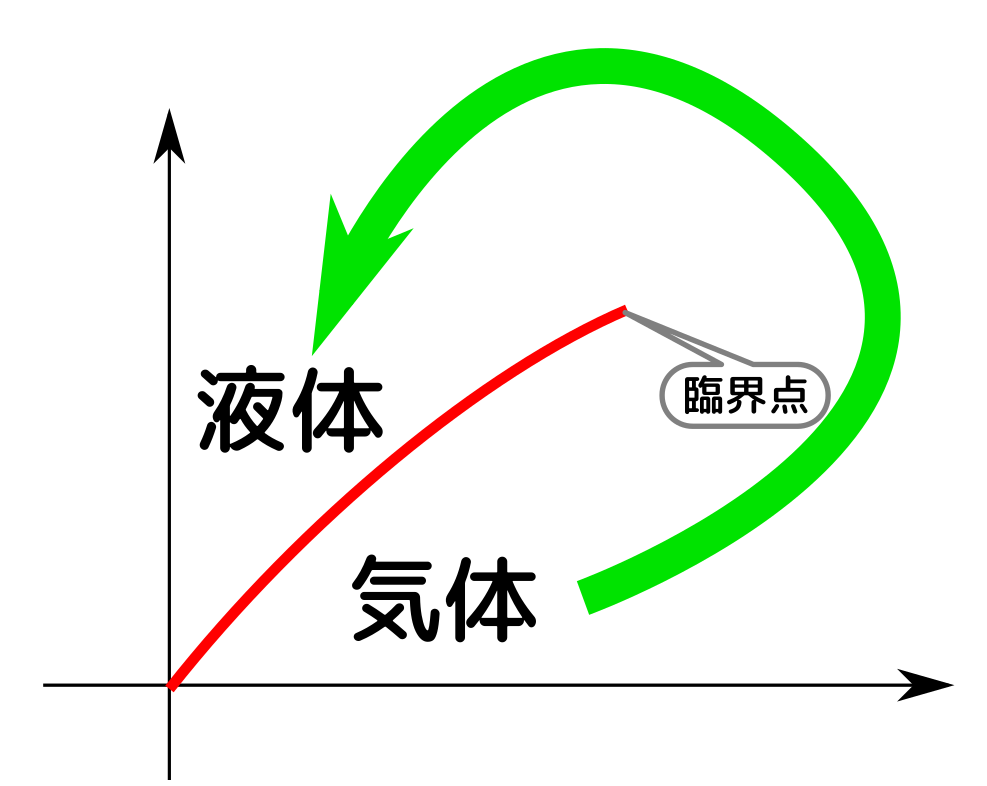
　さらに固体という相も入れると、相図は

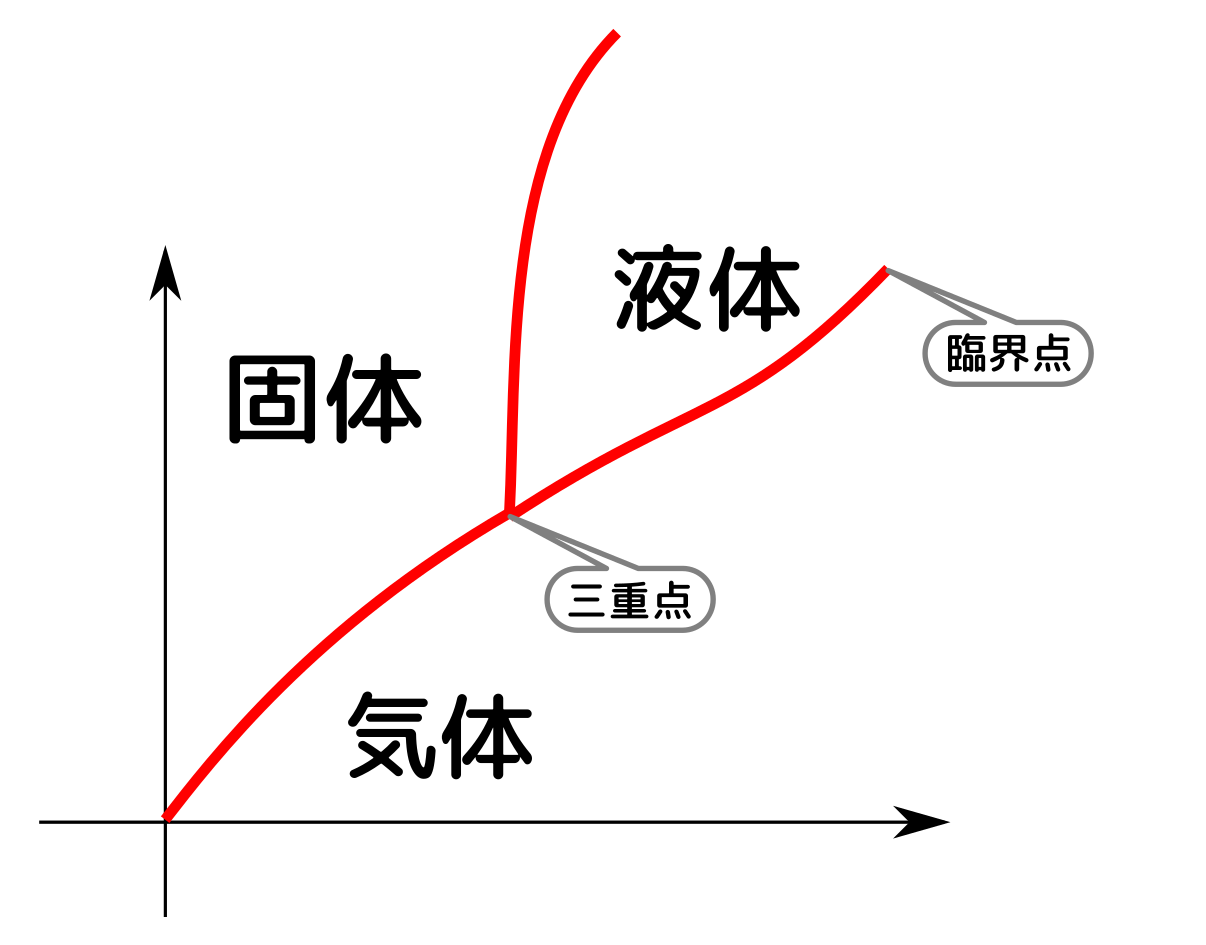
のようになる。三つが共存しているのが「三重点」である。

エンタルピーとギッブス自由エネルギー

液体→気体で吸収する熱

　ある物質が液体の状態$(T;V_{\rm L},N)$から気体の状態$(T;V_{\rm G},N)$と変化したとすると、そのとき熱力学第1法則から、


（内部エネルギーの変化$U_{\rm G}-U_{\rm L}$）＝（最大吸収熱$Q_{\rm max}$）$-$（最大仕事$W_{\rm max}$）


という式が成立するだろう。ところで相転移の時の圧力（一定）を$p_v$と書くことにすると、最大仕事は$W_{\rm max}=p_v(V_{\rm G}-V_{\rm L})$である。

　以上の式を整理すると、 $$ U_{\rm G}+p_vV_{\rm G}-\left(U_{\rm L}+p_v V_{\rm L}\right)=Q_{\rm max} $$ となる。吸収する熱が$H=U+pV$という量の差になっている。

エンタルピー

　この量（内部エネルギー$U$に$pV$を足したもの$H=U+pV$）の物理的意味を考えよう。これの変化がちょうど外部から（熱の形で）与えられたエネルギーになっていることを思うと、$H$は「等圧で断熱された環境におけるエネルギーのようなもの」として機能しているのである。

　そこでこの$H$を「エンタルピー」と読んでエネルギーに似ているがエネルギーとは別の量として扱うことにする（エントロピーと名前は２文字違いだが全然違うものであることに注意すること）。

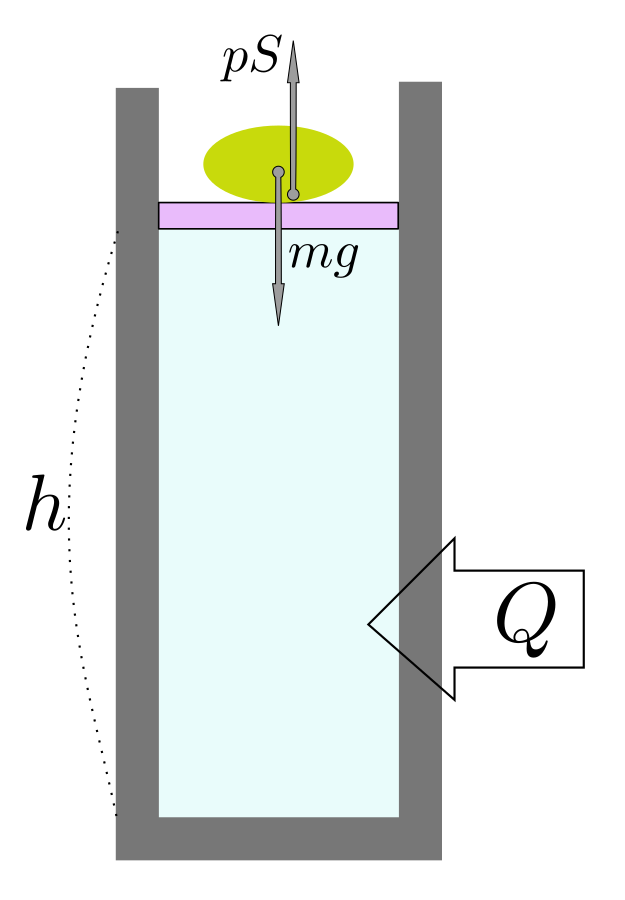
　$H$の物理的意味をもう少し考えてみよう。図のように質量$m$の重りで蓋をされた気体を考える。簡単のために蓋の質量は無視する。また、外部は真空とする（大気圧は0とする）。この物体に働く力のつりあいから、$pS=mg$である。

　この系は質量$m$の重りによってい圧力が$p={mg\over S}$で一定になるように保たれている。このような系に対して熱を与え気体を膨張させたとすると、物体が上に上がるだろう。その物体の位置エネルギーは、与えた熱から提供される。つまり、外部から熱という形で与えられたエネルギーは「気体の内部エネルギーの上昇」と「重りの位置上昇」に消費されることになる。この「重りの位置エネルギー」という系の外にある隠れたエネルギーも含めて熱の移動の収支を考えなくてはいけない。

　そのエネルギーはもちろん$mgh$だが、計算してみると$mgh=pSh$であり、$Sh$が体積$V$であるとすれはこれは$pV$という項そのものである。

　エンタルピーは、この「外部の気体を等圧に保ってくれるもののエネルギー」という「隠れたエネルギー」$pV$を内部エネルギーに足したものだと考えればよい。

　以上から、

のように考えることができる。となると、この手法を「合体」させた、

も考えたくなる。実際、実験室での化学変化などは等温・等圧で行われるから、ギッブス自由エネルギーは重要である。

受講者の感想・コメント

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

　主なもの、代表的なもののみについて記し、回答しています。


化学概論で出てきたG,Hがやっとつながった。
ルジャンドル変換がつなげるのです。

最後に今まで出てきたエネルギーがまとめられて、やっとそれぞれのエネルギーの像がわかった。
それぞれの違いと、使いみちを把握しておきましょう。

もし時間があれば「理解が恋に落ちたので証明してみた」を読んでみてください。
すでに読んでいるけど、う〜ん、そんなに好きな話しではなかったかなぁ。

水鳥の話しですが、頭部がおもくなって下に降りるのですが、元の状態にはどうやって戻るのですか？
今頃？？（今日は水鳥出してないけど）　傾けられたせいで下に落ちるしかけになってます。

エンタルピーの「エン」はエントロピーやエネルギーと同じように「〜の中」みたいな意味なのだろうけど、もうちょっと見分けのつく名前にならなかったのかなと思った。
まぁ確かに紛らわしくはある。

物質量についてのルジャンドル変換はしないのかと思いましたが、物理としてはあまり必要ないのかなと思いました。
化学ポテンシャル$\mu$を独立変数にする計算はあまりしないので、ここまでは出てこないですね。

酢酸ナトリウムの実験は面白かった。
ちょっと不思議ですね。

ここまではテストに対するいい結果をほとんど想像できない。残念。
最後までがんばってください。

dVをdPにするルジャンドル変換はいつやるのかと思っていたがちゃんとHとGとして出てきたので安心した。
これで一応出すべき熱力学関数は出ました。

エンタルピーの持つ物理的意味を理解できた。これもまたルジャンドル変換になっているのが興味深かかった
ルジャンドル変換は役に立ちますね。

だんだん終盤にかけて追い込んでいる感じがした。
あと一回でおわりですね。

授業の内容