今日の講義の内容

　今日から断熱操作に入る。これまでは等温操作における仕事（最大仕事）を考えて、それを元に「ヘルムホルツの自由エネルギー」を定義するところまでだった。

でしばらく遊んでもらった。で、「違いはどこかな？」と聞いてみた。

断熱操作でもゆっくりやるかすばやくやるかで、最後の温度が違う。
断熱操作では一周しても戻らない。
その「戻らない」で、実は温度は上がっている。

などが出てきた。

　上で出てきたように、断熱操作では操作の仕方により到着点が違う。

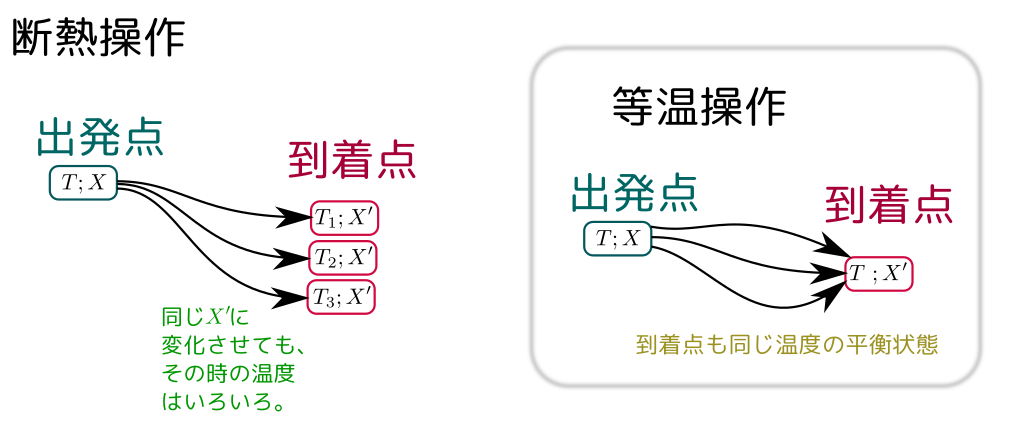
　一方、断熱操作で出発点と到着点をそろえる（つまり、最初と最後で温度が同じ温度になるようにする）場合を図で表現すると、実は以下のようになる。

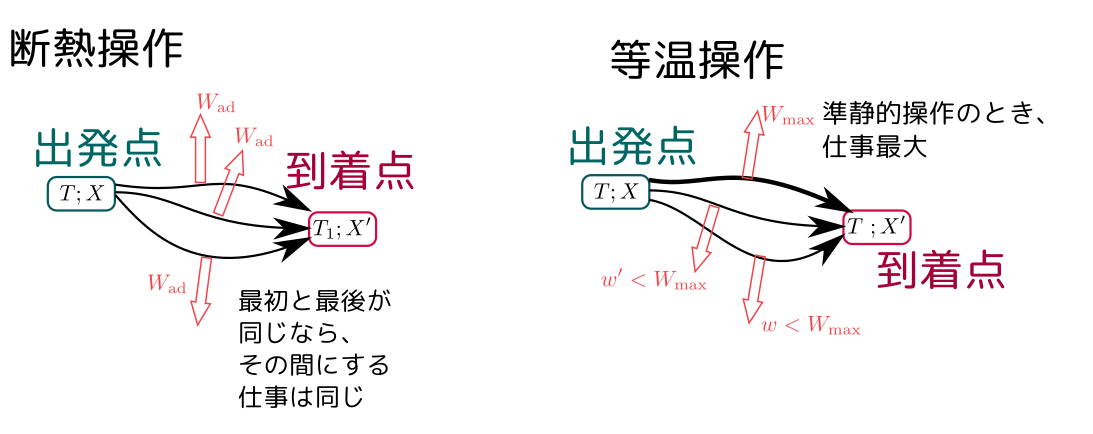
温度を上げる断熱操作の存在

　等温操作では示量変数が元に戻るように操作すると（温度も等温操作の定義により元と同じだから）、その操作はサイクルになった。ところが断熱操作では示量変数$X$が元に戻っても、温度は一般に元に戻らない。つまり、

$(T;X){{\mathrm a}\atop\longrightarrow}(T';X)$

という操作で、$T\neq T'$である。実際に起こる現象を考えると、実は$T\leq T'$である（準静的に行って帰った場合のみ等号が成り立つ）。

　この

「示量変数を変化させずに温度を上げる断熱操作は常に可能」

ということも要請とする。

　寒い時に手をこすると手を温めることができる一方、暑い日に何をしても身体を冷やすことはできない（むしろ動けばもっと暑い）。

断熱操作の存在

　上の例（温度を上げる操作はあるが、下げる操作はない）でもわかるように、断熱操作は常に存在できるわけではない。しかし、$(T;X)\to (T';X')$と$(T';X')\to (T;X)$のどちらかは１つは実現できる。

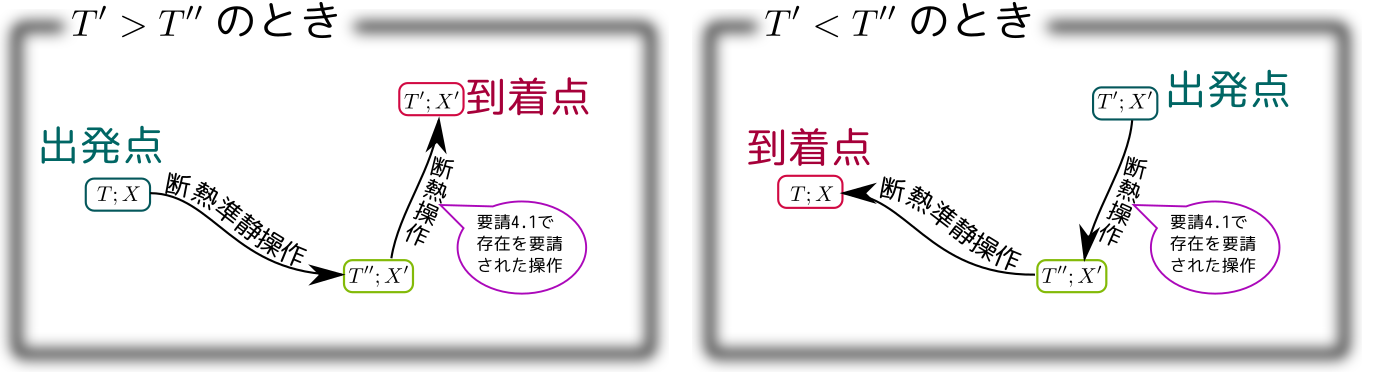
　ここで、$(T;X)\to (T'';X')$という断熱準静操作を考える。もし、$T'$＞$T''$なら、あとは温度を上げるだけなので、上の要請で存在を要請された温度を上げる断熱操作をすれば$(T';X')$に到着する。

　もし$T'$＜$T''$なら、その時は要請により$(T'';X')\to(T';X')$は必ず存在する。そして$(T;X)\to (T'';X')$という断熱準静操作は（準静的なので）逆が存在するから逆をたどればよい。こうして、どちらの操作も可能になる。

両方が可能になるのは、最初から断熱準静操作でつながっていた場合に限る。

　なぜここで「断熱操作が存在すること」にこだわるかというと、我々は「エネルギーを定義」したいのであり、そのためには「ある状態からある状態へ変化させるときの仕事」を考えなくてはいけないが、そもそも「ある状態からある状態へ変化」させることができないならそんなことを考えても無意味なのである。

　断熱操作は「仕事以外のエネルギーの出入りがない」状況を考えているので、エネルギーはちょうどした仕事の量だけ増減する（等温操作ではそうではなかったことに注意）。

　そのためにはもちろん、（力学で位置エネルギーが定義できる条件がそうであったように）「はじめの状態と終わりの状態が決まればその間にする仕事は１つに決まる」という条件が成り立っていなくてはいけない。力学の場合、系が質点や剛体でできていて摩擦や空気抵抗がなく保存力しか働かないならこれは導くことができる定理になる。しかし熱力学ではこうなることも要請にしておく。

断熱操作で系が行う仕事は、最初と最後の平衡状態だけで決まり、途中経過によらない。

　この、「最初$(T;X)$と最後$(T';X')$が決まれば途中経過によらず決まる仕事の量」を$W_{\mathrm ad}\left((T;X)\to (T';X')\right)$と書いて「断熱仕事」と呼ぶことにする。断熱仕事は最大仕事と同様に、示量性と相加性を持つ。

　こうして我々は、熱力学でも「エネルギー」を定義できるようになった、というわけ。

　さて、先週は

　等温操作での最大仕事の分だけ、ヘルムホルツ自由エネルギーが減る。式で書けば

等温準静操作で $$ \mathrm dF= -P\mathrm dV $$ または $$ P=-{\partial F\over\partial V} $$

というところまでやった。今週やったことは

断熱操作で $$ \mathrm dU= -P\mathrm dV $$ または $$ P=-{\partial U\over\partial V} $$

ということ。ここで「偏微分の意味」に注意が必要で、$P=-{\partial F\over\partial V}$の${\partial\over\partial V}$は「$T$を一定として$V$で微分」であった。一方$P=-{\partial U\over\partial V}$の${\partial\over\partial V}$は一体何を一定としての$V$微分なのだろう？？

　この答えは、もう少し後で。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

　主なもの、代表的なもののみについて記し、回答しています。

要請4.3で経路によらず仕事が決まるところは力学に似ていると思った。

この部分は全く力学と同じ考え方ですね。

準静的な操作の重要性が等温操作より低いなと思った。

いやいや、それはまだ準静的断熱操作の大事さを語ってないからです。

力学でのエネルギー保存則は導かれるけど熱力学では要請として出されるところが興味深かった。

熱力学の方がそれだけ、使う範囲が広くなっています。

前回までの進捗に比べてかなり上がったので良いと思います。

ほんとはもう少しは行きたかったんだけどね。

内部エネルギーと自由エネルギーの変化はどちらも$-P\Delta V$だとわかった。

「どういう状況で」の部分が全然違うのです。

ようやく熱が定義できそうなので楽しみ。

次回ですね。

熱力学は偏微分を使用するので練習しとこう。

偏微分は使いまくりです。

力学と全然違うなぁ〜。

力学と考え方は同じで、でも扱う相手が違うから違ってくる。

梅雨入りしたので大変です。

この後は夏だしね。

断熱操作のとき仕事は経路によらず出発点と行先が同じなら等しいというのが等温操作とのちがいだとわかった。

そこは大事。

内容が難しいので、理解できるまでノートとにらめっこします。

教科書もじっくり読みましょう。

最後の$P=-{\partial U\over\partial V}$が何を一定にして微分しているのかが気になりました。

「引き」として言っておいたんですが、成功したようです。もうすぐわかりますから、それまでお楽しみに。

授業の内容