今日の講義の内容
今日はカルノーの定理の証明。
カルノーの定理はカルノーサイクルの吸熱と排熱の比${Q_{\rm out}\over Q_{\rm in}}$が温度の比${T_{\rm out}\over T_{\rm in}}$に等しいというものだが、これを次の2段階に分けて示そう。
- 同じ熱源を使うカルノーサイクルであればすべて吸熱比${Q_{\rm out}\over Q_{\rm in}}$が等しいこと
- 理想気体を使ったカルノーサイクルでは吸熱比が${T_{\rm out}\over T_{\rm in}}$になること
そのために、まず同じ熱源で動くカルノーサイクルを二つ考える。
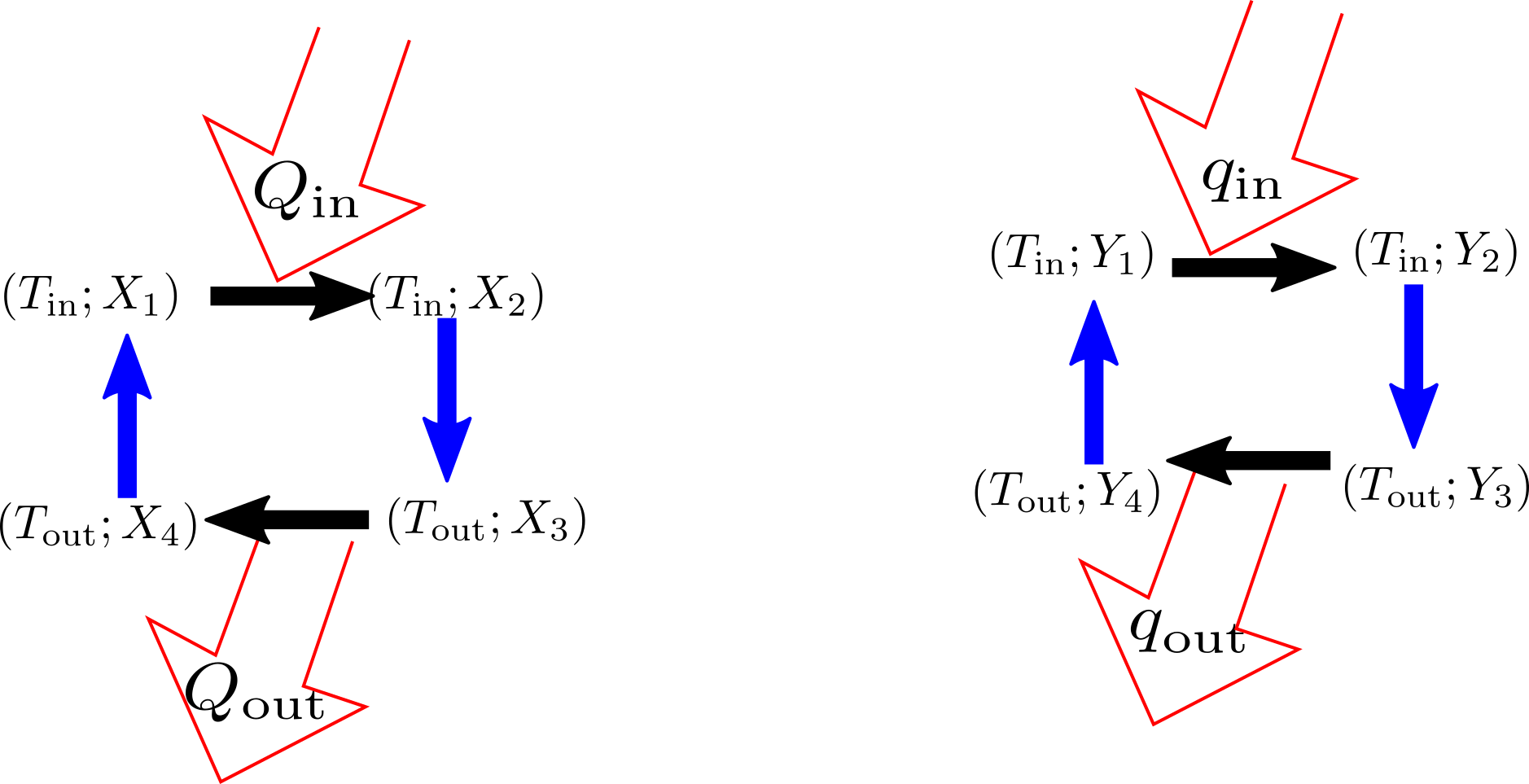
Kelvinの原理を使ってカルノーの原理を示したいが、Kelvinの原理は「一つの温度$T$の中で動くサイクルがする仕事は0以下」というものであった。カルノーサイクルは二つの温度$T_{\rm in},T_{\rm out}$の中で動くから、そのままでKelvinの原理は使えない。そこで、いわば「$T_{\rm out}$で起こることを打ち消す」方法を考える。
そのため、まず$Y_1$→$Y_4$の方のカルノーサイクルを逆回転させる。
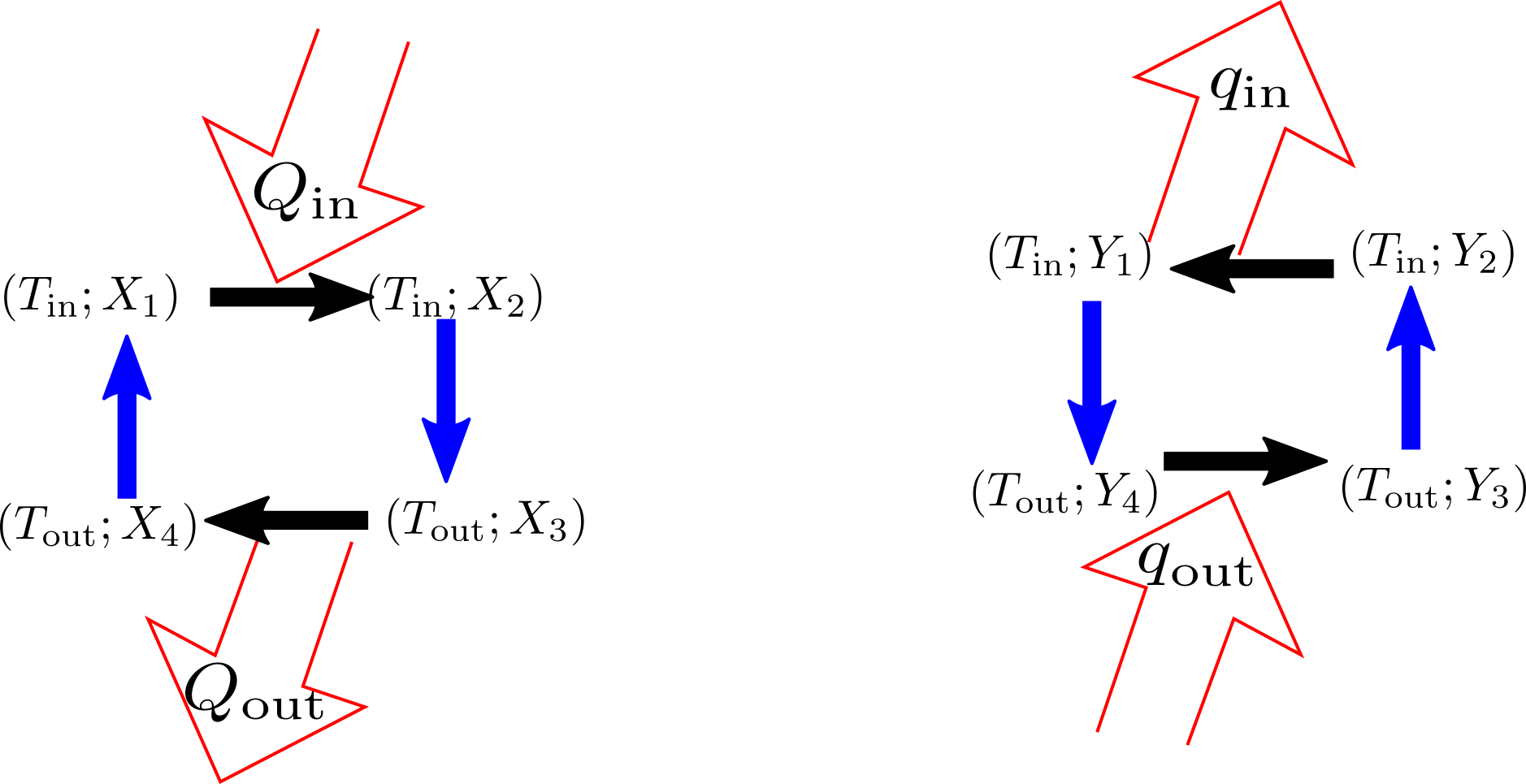
するとこのサイクルは温度$T_{\rm out}$において$q_{\rm out}$の熱を吸い込む。$Q_{\rm out}$と$q_{\rm out}$が一致しない場合、$Q_{\rm out}=\alpha q_{\rm out}$が成り立つ数を$\alpha$として、$\alpha$個の$Y$-逆回転カルノーサイクルを持ってくる。
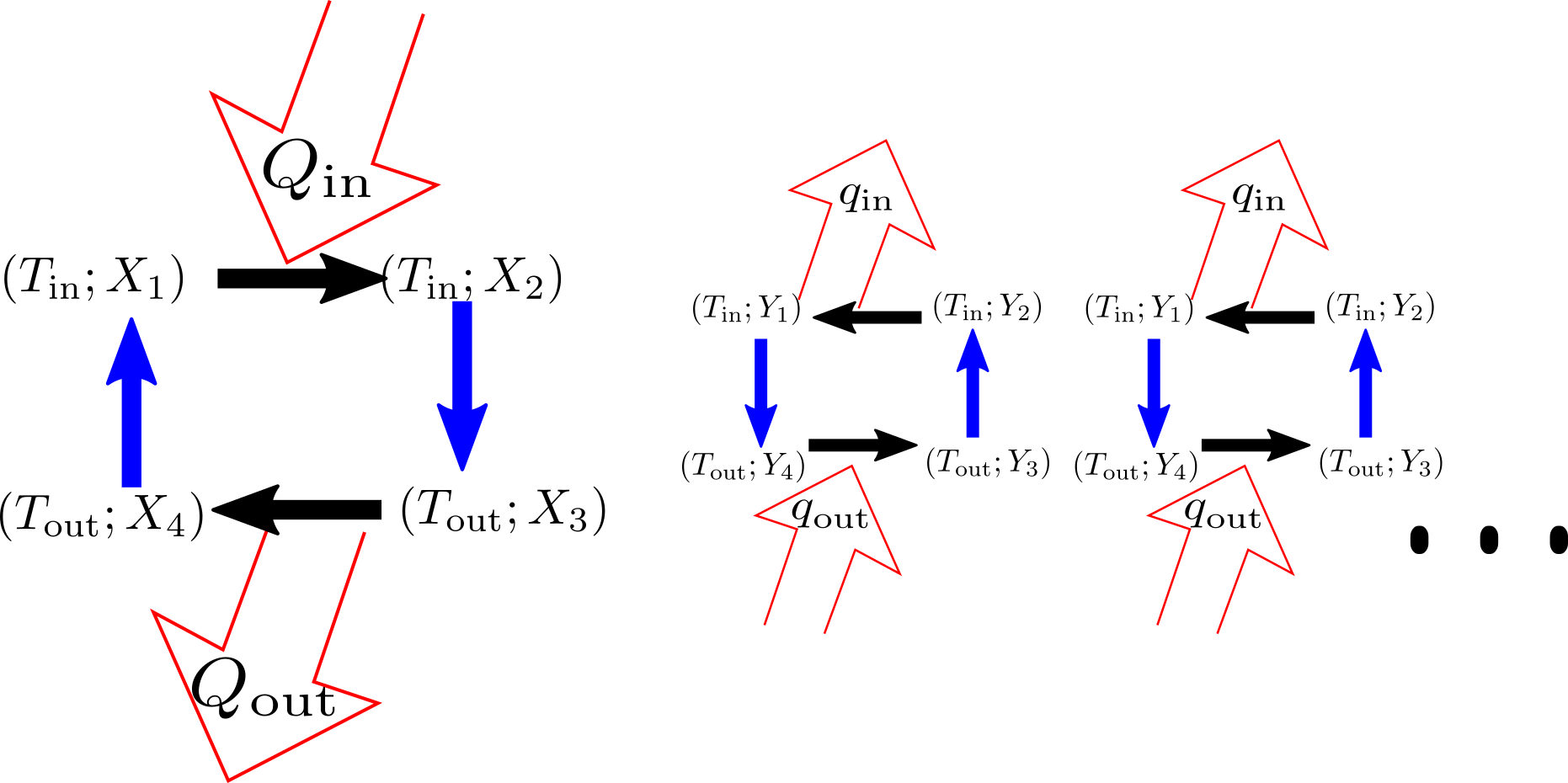
これで$X-\alpha Y$のカルノーサイクルは温度$T_{\rm out}$の熱源には熱を放出も吸収もしないことになる。その部分をブラックボックス化して隠してしまったのが次の図である。
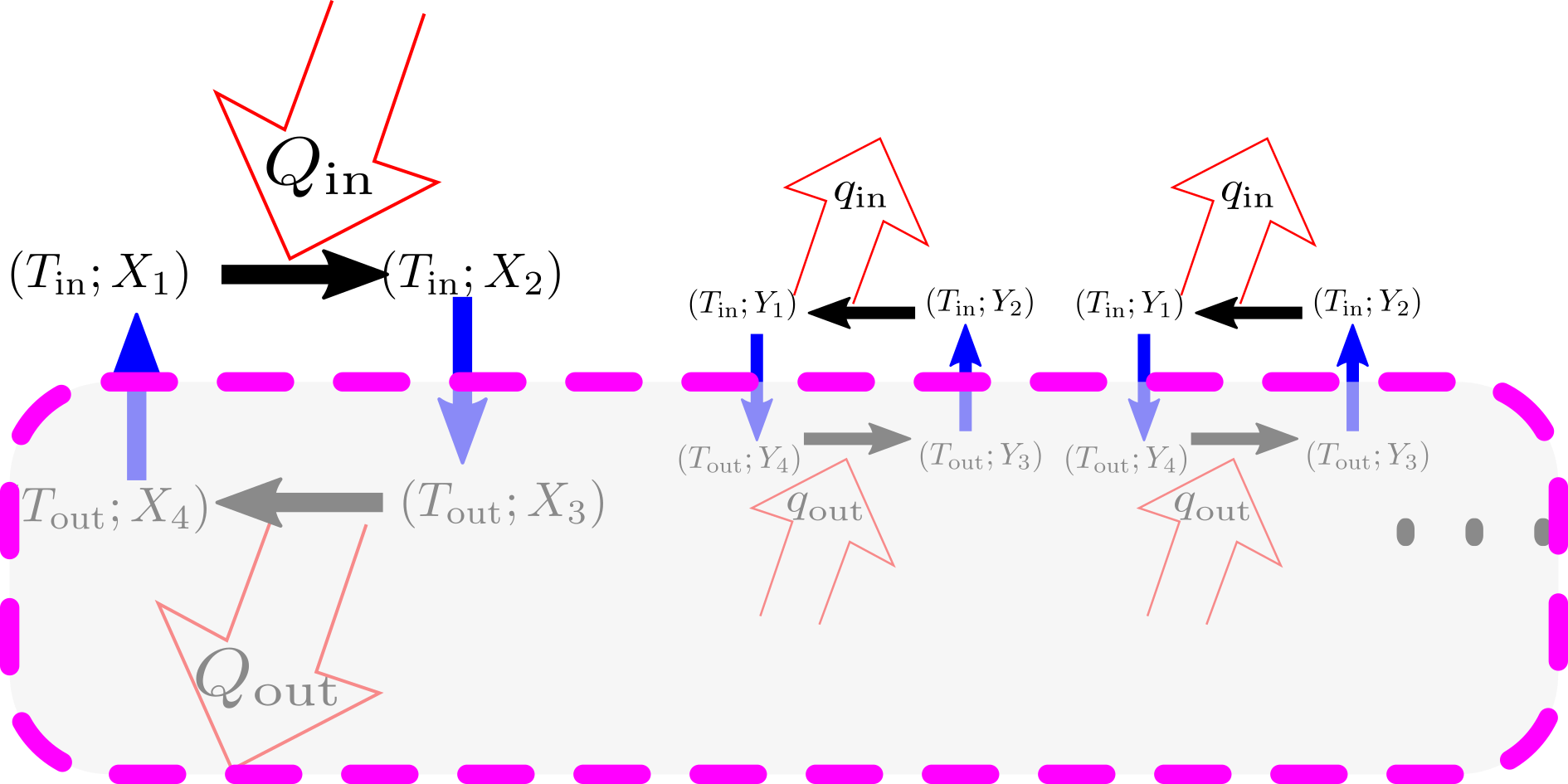
とはいえ、実際には熱を吸ったり吐いたりしてトータルで吸熱0になっているのとこれは違うのでは??という疑問が湧くかもしれないが、それについては教科書の著者の田崎さんがCarnot の定理の証明(5-4 節)の改良についてという説明(よりわかりやすい証明になっている)を書いているのでこの中の文書をプリントして配った(とはいえ、学生さんの持っている本の多くはすでにこの改良が入った版であった)。
というわけで温度$T_{\rm out}$の環境は「なくてもいいこと」になったので、ここでKelvinの原理を使う。$X$のカルノーサイクルのする仕事を$W$、$Y$のカルノーサイクルのする仕事を$w$とすれば、$X-\alpha Y$のカルノーサイクルは$W-\alpha w$の仕事をする。これは温度$T_{\rm in}$の環境のなかでのサイクルとみなしていいから、$W-\alpha w\leq 0$でなくてはいけない(Kelvinの原理)。カルノーサイクルは逆回転できるから、同じことを逆回転して考えると$W-\alpha w \geq 0$も示せる。これは$W-\alpha w=0$ということで、これから$Q_{\rm out}$の比も、仕事$W$の比も$\alpha$で共通であることがわかり、当然$Q_{\rm in}$の比も$\alpha$である。これから${Q_{\rm out}\over Q_{\rm in}}={q_{\rm out}\over q_{\rm in}}$が示せた。
次に理想気体の場合でカルノーサイクルを回すと、${Q_{\rm out}\over Q_{\rm in}}={T_{\rm out}\over T_{\rm in}}$がわかる。こうして、カルノーの定理が示せた。
次に、を動かしてもらって、特に「$V$-$P$グラフ」だけではなく「$V$-$T$グラフ」を見てもらった。
ここでく「$V$-$T$グラフ」では等温操作が「水平線」になって、温度が一定であることがわかりやすい。ここで「断熱線が垂直線になったら幸せがあるんじゃなかろうか?」と考える。そして、「断熱線が垂直線になるような横軸って何?」と考えてみよう。
「断熱線が垂直になる(断熱操作の間横軸が変化しない)」んだったら、横軸は熱そのものを目盛りにすれば?---と考えたくなるかもしれないが、二つの等温操作での吸熱・排熱は等しくないから、それでは長方形にならない。長方形にするには、今日の話からして、熱を温度で割った量が使えそうだ。
では何を横軸にするといいかというと、それが「エントロピー」である。これについてはまた来週。