今日の講義の内容
いよいよエントロピー。
もう一度、を動かしてみるところから始めた。前回は
というところまで考えた。つまり、「断熱準静操作では一定に保たれる変数」を作ろう、ということである。
カルノーサイクルは等温操作と断熱操作を組み合わせているが、その等温線と断熱線を、$V$-$P$グラフ上に表現したものを見てみよう(↓は静止画)。
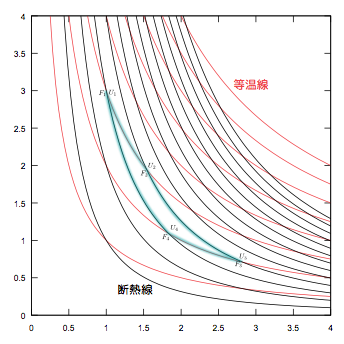
ということに気づいて欲しい。どちらの線も曲線で、しかもよく似ているのだから少々見た目がわかりにくい。そこで等温線の方だけを水平にしよう(それは簡単で、縦軸を温度$T$にすればよい)。グラフを次に載せよう。

この横軸(体積$V$)を適当にスケールして、軸を水平・垂直な格子状にすることもできるのは?---つまり、
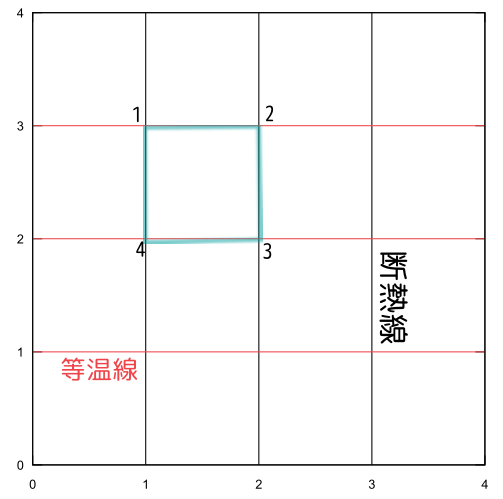
のようなグラフを作りたい!!という「野望」を抱こう。
そういう量が見つかるためには、
- 図の$2\to3$と$4\to1$で「変化量」が0。
- 図の$1\to2$での「変化量」の積分と、$3\to4$での「変化量」の積分が逆符号で絶対値が同じ。
という二つの条件が満たされなくてはいけない。別の言い方をすれば「変化量」をサイクルで一周積分すれば0にならなくてはいけない。
たとえばその変化量として熱量$Q$を使う---というのはまずいアイデアである。というのは$1\to2$で吸収する熱量と$3\to4$で放出する熱量は絶対値が一致しない。逆符号で同じ大きさにはなってない。
ここでこれらの量の間に他に条件式はなかったっけ?---と思い出してみると、Carnotの原理により、 \begin{equation} {Q_{\mathrm out}\over Q_{\mathrm in}}={T_{3\to 4}\over T_{1 \to 2}} \end{equation} あるいは、 \begin{equation} {Q_{\mathrm out}\over T_{3\to 4}}={Q_{\mathrm in}\over T_{1 \to 2}} \end{equation} があるから、$\Delta S={Q\over T}$のような変化をする量$S$を定義すると、ちゃんと$1\to2$での変化と$3\to4$での変化が逆符号で消し合うことになりそうだ。
等温操作での吸熱量は$U$の変化と$F$の変化の差であるから、$Q_{\mathrm in}=(U_2-U_1)-(F_2-F_1)$と$Q_{\mathrm out}=(U_3-U_4)-(F_3-F_4)$($Q_{\mathrm out}$の方は引き算の方向が逆だが、これはinとoutの違い)という式が出る。これを代入すれば、
\begin{equation} {(U_3-F_3)-(U_4-F_4)\over T_{3\to 4}}={(U_2-F_2)-(U_1-F_1)\over T_{1 \to 2}} \end{equation} となる。ここで、${U-F\over T}$という量を$S$と書くことにすれば、 \begin{equation} S_3-S_4 = S_2 - S_1 \end{equation} なる式が出てくる。この式は「過程$1\to 2$における$S$の変化」と、「過程$3\to4$における$S$の変化」が等しいという式になっている。
そういうことができるのは、ここまでは$F$を「等温準静操作でした仕事の分減る量」とのみ定義して「温度が変化するとどう変わるか」を決めていなかったからである(たとえば理想気体でどう決めればいいかは、後でやろう)。
このようにして決めた新しい状態量が$S$すなわちエントロピーである。
エントロピーの性質
エントロピーが示量変数で相加性を持つことは、$U,F$および$U,F$の定義に使った仕事という量が示量的で相加的であることを考えるとすぐに納得できる。また、断熱準静的操作で変化しないということも、ここで説明した作り方からすれば納得がいく。
次に大事な性質として、
$S(T;V)$<$S(T';V)$
が成り立つ。また、(それぞれの変数が微分可能なら)
$\displaystyle {\partial U(T;V)\over \partial T}=T{\partial S(T;V)\over \partial T}$
が成り立つ。
がある。
これを証明するために、次の図のような二つの操作を考える。
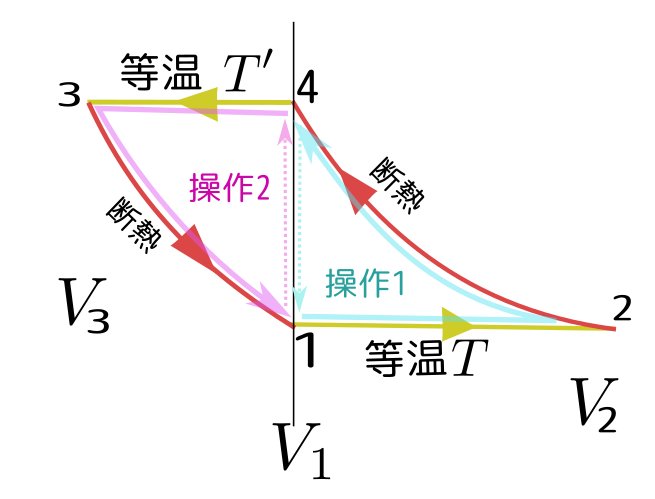
ここで、操作1の4→1は、外界の温度(常に$T$)に接触した系(その前の段階で温度は$T'$になっていた)の温度が$T$に一致するまで待つ、という操作である(外界は常に温度$T$であることに注意)。
操作2の1→4も同様で、この場合は外界の温度が常に$T'$で、系の温度がそれに一致していく。
上の操作1(1→2→4→1)の一周において系のする仕事は、
$W_{\mathrm cyc}=\left(F(T;V_1)-F(T;V_2)\right)+\left(U(T;V_2)-U(T';V_1)\right)$
と書けるが、いまや$F=U-TS$となったことを使うと、
$W_{\mathrm cyc}={F(T;V_1)-F(T;V_2)}+U(T;V_2)-U(T';V_1)={U(T;V_1)-U(T;V_2)-T(S(T;V_1)-S(T;V_2))}$
となり、ここで$-U(T;V_2)+U(T;V_2)$を消して、さらに$S(T;V_2)=S(T';V_1)$を使うと、
$W_{\mathrm cyc}=U(T;V_1)-T(S(T;V_1)-S(T';V_1))-U(T';V_1)$
となる。体積$=V_1$という、1つの体積について式が出せたことに注意。
ここで、環境(外界)の温度は常に$T$だったことを考えると、ケルビンの原理により、$W_{\mathrm cyc}\leq 0$だから、
$U(T;V_1)-U(T';V_1)-T(S(T;V_1)-S(T';V_1))\leq 0$
よって、
$T(S(T';V_1)-S(T;V_1))\leq U(T';V_1)-U(T;V_1)$
となる。同様に操作2(4→3→1→4)を考えると、
$W_{\mathrm cyc}={F(T';V_1)-F(T';V_3)}+{U(T;V_1)-U(T';V_3)}$
から、
$W_{\mathrm cyc}=U(T';V_1)-T'(S(T';V_1)-S(T;V_1))-U(T;V_1)$
となって、これが$\leq0$であることから、
$U(T';V_1)-U(T;V_1)\leq T'(S(T';V_1)-S(T;V_1))$
が言える。
この二つをまとめて考えて、
$T(S(T';V_1)-S(T;V_1))\leq U(T';V_1)-U(T;V_1)\leq T'(S(T';V_1)-S(T;V_1))$
$T'\to T$になる極限(つまり、$T'-T=\Delta T\to0$となる極限)を考えると左辺も右辺も$T{\partial S(T;V)\over\partial T}\Delta T$へと接近する(中辺は${\partial U\over\partial T}\Delta T$になる)ので、
${\partial U\over \partial T}=T{\partial S\over \partial T}$
が言える。
このこと(つまり、内部エネルギーの$T$微分とエントロピーの$T$微分が、比例定数$T$で比例すること)からエントロピー$S$が温度の増加関数であることがわかる。
この式は(ちょっと示すのに時間を掛けてしまったが、そもそもエントロピーが$\Delta S={Q\over T}$となるように定義されていたことを思えば、出てきて当然の式である。