試験とその解答
必須問題1

答えはここをクリック
それぞれの物理量が状態量(stock)か、変化量(flow)か、さらにflowだとして途中経過によるか、を訪ねている。
(1)ウ(2)ア(3)ア(4)ウ(5)ウ
が答え。
基本中の基本を聞いたつもりだが、これを間違えているようでは先が思いやられる。ここがわかってないと熱理学全然わかってないに等しい。

答えはここをクリック
「水が液体から気体に変わるときにエントロピーが増えている」というのが一番重要な点で、最低でも「水のエントロピーが増えている」と答えて欲しいところ。
この人の問いは「どこでエントロピーが増えているのでしょう?」であるので、という方向で答えてほしい。
「エントロピーが増大するのは断熱操作のときだけである」と答えていた人がいたが、それではこの人の疑問に答えたことにはならない。

答えはここをクリック
「どこを間違ったのか?」に対しては2種類の解答がある。
- 圧力一定で温度が上昇すると、気体は膨張するので仕事をする。よってそのときに必要な熱を計算するときは仕事を足さなくてはいけないが、それを忘れている。
- 定圧の操作を考えているのだから、内部エネルギー$U$ではなくエンタルピー$H$を使って熱を計算すべきである。
どちらかが正解だが、下の回答例が多かった。
「$U(T;V)$や$U(T,P)$は完全な熱力学関数ではないから」という回答がいくつか見られたが、そんなことは全く関係ない。

答えはここをクリック
クーラーをサイクルと考えるので、クーラーは元の状態に復している。室外機がないということは外に熱を出さないので断熱操作である。それなのに温度が下がるとしたら、プランクの原理あるいはエントロピー増大の原理に反しているということがかけていれば正解。
「カルノーの原理から、温度差がないと仕事はできません」と書いている人がいたが、この場合はクーラーは外から仕事をしてもらっているのだから、それとは関係ない。
答えはここをクリック
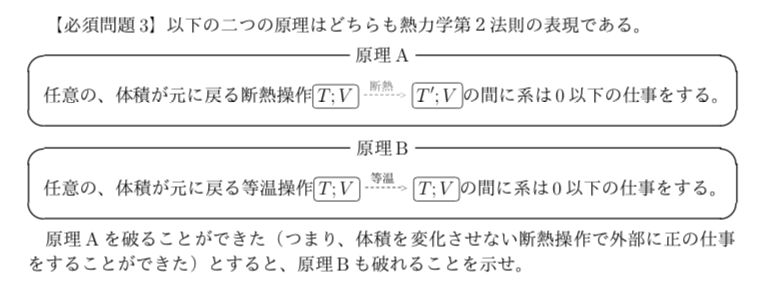
原理Aを破る機械が存在していたとすると、$T;V$から$T';V$へと断熱操作して系にプラスの仕事をさせた後、その後系を温度$T$の熱浴に接触させて温度$T$になるまで待てば、状態$T;V$から$T;V$へと等温の環境の中で正の仕事ができたことになる。よって原理Bも破れる。

答えはここをクリック
(1)$P=-{\partial F\over\partial V}=NRT\times\alpha{2V\over N^2}={2\alpha RV\over N}$
(2)$G=F+PV=NRT\left(1-\alpha{V^2\over N^2}\right)+PV$として、ここで終わっている人がいたが、$G[T,P;N]$にLegendre変換せよ、という問題なんだからちゃんと$T,P;N$で表すところまで計算しよう。(1)の結果より$V={PN\over 2\alpha RT}$であるから、$G=NRT\left(1-\alpha{P^2\over 4\alpha^2 R^2T^2}\right)+{P^2 N\over 2\alpha RT}=NRT +{P^2 N\over4\alpha RT }$となる(ここでここまでちゃんと計算しておかないと、次の(3)でおかしなことになるのだ)。
(3)${\partial G\over \partial P}=V$となるはずである。微分すると、${\partial G\over \partial P}={PN\over 2\alpha RT}$で、確かに$V$になる。
これを上の(2)で計算を途中で放り出して「$G=NRT\left(1-\alpha{V^2\over N^2}\right)+PV$を$P$で微分したら$V$」とやっている人がいたが、これは全く駄目な計算。独立変数は$T,P;N$としているのだから、ここでは$V$は$P$の関数なのである。
もっと駄目な計算として、$PV=NRT$を代入している人がいた。この系が理想気体だなどとは、一言も言ってない。

答えはここをクリック
「本来持っていなければいけない性質」とは「下に凸であること」。これがないと不安定になる。不安定になり理由は体積が増加すると圧力が増えるのでどんどん体積が増えてしまう、というのでもよいし、「エネルギー最小」が決まらなくなるということでもよい。

答えはここをクリック
二つのカルノーサイクルを一方を逆回転させて結合し、一方の排熱を利用してもう一方を動かす。すると一つの熱源とのみ熱のやりとりをするサイクルができあがる。効率が違うという前提が正しければ、このとき仕事は0ではない。負であったとしたらサイクル全体を逆回転させれば正の仕事が得られる。これは熱力学第2法則(Kelvinの原理)に反する。

答えはここをクリック
(1)$\left({\partial H\kakko{T,P}\over \partial P}\right)_T=\left({\partial H\kakko{P;S}\over \partial P}\right)_S+\left({\partial H\Kakko{P;S}\over \partial S}\right)_P\left({\partial S\kakko{T,P}\over \partial P}\right)_T$
(1)の答えに、$\left({\partial H\Kakko{P;S}\over \partial P}\right)_S=V$と$\left({\partial H\kakko{P;S}\over \partial S}\right)_P=T$、および$\left({\partial S\kakko{T,P}\over \partial P}\right)_T=\left(\partial V\kakko{T,P}\over \partial T\right)_P$を使うと、$$-V+T\left({\partial V\kakko{T,P}\over \partial T}\right)_P=0$$であれば右辺が0になることがわかる。
これは、$U$に関するエネルギー方程式と同じものを、$H$に関して導いてもらうという問題でした。

答えはここをクリック
二階微分の順序を替えたものが等しいという関係式を作る。 $$ {\partial\over\partial T}\left({\partial G\over\partial P}\right) ={\partial\over\partial P}\left({\partial G\over\partial T}\right) $$ より、${\partial V\over\partial T}=-{\partial S\over\partial P}$。
$$ {\partial\over\partial N}\left({\partial G\over\partial P}\right) ={\partial\over\partial P}\left({\partial G\over\partial N}\right) $$ より、${\partial V\over\partial N}={\partial \mu\over\partial P}$。
$$ {\partial\over\partial N}\left({\partial G\over\partial T}\right) ={\partial\over\partial T}\left({\partial G\over\partial N}\right) $$ より、$-{\partial S\over\partial N}={\partial \mu\over\partial T}$。
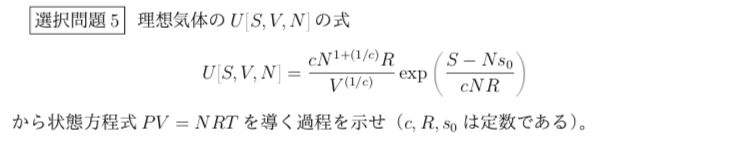
答えはここをクリック
$P=-{\partial U\over\partial V}=-{N^{1+(1/c)}R\over V^{1+(1/c)}}\exp\left({S-Ns_0\over cNR}\right)$と$T={\partial U\over\partial S}={cN^{1+(1/c)R}\over V^{(1/c)}}\times {1\over cNR}\exp\left({S-Ns_0\over cNR}\right)$から、$P={NRT\over V}$が出てくる。
これは、単純な計算問題。なお、$U=cNRT$をいきなり使っている人がいたが、この問題はそれも含めて導いて欲しいところ。

答えはここをクリック
(1)$p={NRT\over V}$なので、$\int_{V_1}^{V_2}p\diff V=NRT\int_{V_1}^{V_2}{\diff V\over V-b}=NRT\log\left({V_2-b\over V_1-b}\right)$
(2)$\Delta U=Q-W$で、$W$が上の答え。$\Delta U=0$(等温だから)。よって(1)の答えそのものである。
(3)断熱操作だから内部エネルギーの変化で決まるが、今は温度が変化しないのだから、0
(4)断熱操作だから、$\diff U=-p\diff V$となり、$NcR\diff T=-{NRT\over V-b}\diff V$という式が成立する。 変数分離して$c{\diff T\over T}=-{\diff V\over V-b}$なので積分して、$c\log T=-\log (V-b)$となり、一定となるのは$T^c (V-b)$という量(または、$T(V-b)^{1\over c}$などでもよい)。あるいは状態方程式から$T={p(V-b)\over NR}$だから、$p(V-b)^{1+{1\over c}}$が一定。

答えはここをクリック
(1)$0=\diff S=(U-F)\times\left(-{\diff T\over T^2}\right)+{1\over T}(\diff U-\diff F)$に$\diff U=-P\diff V$を代入すると、$0=-{U-F\over T}{\diff T\over T}+{1\over T}(-P\diff V-\diff F)$となって、これから$\diff F=-S\diff T-P\diff V$
(2)$0=\diff T=(U-F)\times\left(-{\diff S\over S^2}\right)+{1\over S}(\diff U-\diff F)$に$\diff F=-P\diff V$を代入すると、$0=-{U-F\over S}{\diff S\over S}+{1\over S}(\diff U+P\diff V)$となって、これから$\diff U=T\diff S-P\diff V$