2005年度初等量子力学試験

＊プランク定数h、hbar.png= [h/2π]など、必要な物理定数は解答に使用してよい。
＊計算の過程も解答用紙に書くこと（公式覚えてきて書いただけでは点はやれないし、途中が書いてないと部分点もあげられない）。
以下の問のうち、４問を選択して解答せよ。５問以上答えた場合は点数のいい方から４つを合計して点数とする。


[問い1] 量子力学を勉強中の下級生にこう質問されたら、あなたはどう答えるか。ほんとに下級生に教えるつもりで、質問した人に納得してもらえるように丁寧に書くこと。
  1. 「『波動関数ψ = e[i/((h/2p) )](px−Et)はxの正の方向に運動量p を持った状態だ』と本に書いてあるんですが、この波動関数から確率密度を計算すると、ψ*ψ = 1になっちゃいました。『運動量を持っている』って言うのに、確率が場所にも時間にもよらないってどーゆーことですか」
  2. 「ψ = e[i/((h/2p) )](px−Et)という式でもう一つ質問なんですけど、このEはエネルギーで、1/2mv2ですよね。p=mvとすると、この式の位相は[1/hbar.png ](mvx−1/2mv2t)=[mv/hbar.png](x−1/2vt)となりました。これだと波の速度が1/2vになっているんですけど、運動量mvなのに速度vにならないのはなぜですか？」
  3. 「量子力学ではエネルギーは振動数×プランク定数(hν)になりますよね。じゃあエネルギー0だと振動しないということですよね。古典力学ではエネルギーの原点はどこでもいいから、E→ E+E0のように定数だけずらしてもいいという話だったけど、量子力学では振動が止まっている時がエネルギーが0ということで、エネルギーの原点決まっちゃうんですか？」
解答例へ


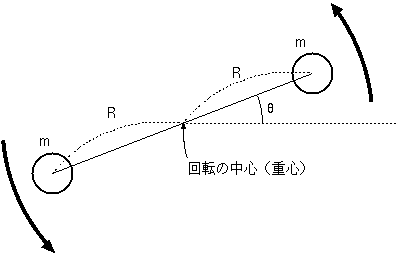[問い2] 二原子分子の回転H2,O2の ような２原子分子の回転運動を量子力学で扱うとどうなるかを考えよう。質量mの二つの粒子が距離2Rだけ離れて結びついているとする。実際の回転は３次元 的に起こるが、ここでは簡単のため平面上をぐるぐる回るとし、それ以外の運動は全て無視する。図の角度をθとして、θ に対する運動量をpθ とすると、これは角運動量であるから、pθ=2mR2· θである。
 
　シュレーディンガー方程式を作る時にはハミルトニアンのpθを−ihbar.png[∂/∂θ]と置き換えればよい。
  1. この回転運動に対するシュレーディンガー方程式が
    − hbar.png2
    4mR2
    		∂2
    ∂θ2
    		 ψ(θ,t) = ihbar.png ∂
    ∂t
    		 ψ(θ,t)
    となることを説明せよ。
  2. 解の形をψ(θ,t)=Aeilθ−iωtと仮定し、この方 程式を解いて、lとωの関係を求めよ。
  3. 波動関数が規格化された状態であるためには、Aはいくらでなくてはいけないか。
  4. θ = 0とθ = 2πは同じ状態であるから、波動関数ψ(θ)はψ(0)=ψ(2π)を満たさなくてはいけない。このことからlにはどんな条件が付くか。
  5. 気体分子運動論によれば、絶対温度がTの時、運動の１自由度ごとに1/2kTのエネルギーが分配されるので、このエネルギーの平均値も1/2kT程度になるはずである。しかし温度が低い時、それだけのエネルギーは分配されなくなる。なぜそうなるのか、理由を説明せよ。
解答例へ


[問い3] 解析力学のハミルトン形式では、座標x、運動量p、ハミルトニアンHの間に、

dp
dt
 =− ∂H
∂x
 ,     dx
dt
 = ∂H
∂p
という正準方程式が成立していた。
一方量子力学のシュレーディンガー方程式は
ihbar.png ∂
∂t
 ψ = Hψ
という形をしている。
正準方程式が量子力学ではどのように実現されているかを数式を使って具体的に 述べ、その証明を与えよ。
解答例へ

[問い4]
  1. 光電効果は、光の粒子性を示す実験であるとよく言われる。この実験のどのような点が光の粒子性の顕れなのかを説明せよ。ただし、
    • 光を波だと考えると、どのような実験事実に反することになるのか。
    • 光子一個のエネルギーがhνであるという事実は、実験結果のどこに あらわれているか。
    の二つの論点について必ず述べること。
  2. 光電効果以外の、光の粒子性を示す実験事実を一つあげ、その実験事実 のどこが光の粒子性の顕れなのか、説明を述べよ。
解答例へ


[問い5] 質量mの粒子の物質波が領域Iから領域IIへと入射した。 領域Iでは位置エネルギーはVだが、領域IIでは0である（V > 0とする）。領域I、領域IIでのシュレーディンガー方程式はそれぞれ、
ihbar.png ∂
∂t
ψI = [ − hbar.png2
2m
∂2
∂x2
 +V] ψI
と
ihbar.png ∂
∂t
ψII = − hbar.png2
2m
∂2
∂x2
 ψII
である。
  1. 解としてψ = A eikx−iωtという形を仮定する(A,k,ω は定数)。kとω の間に成立する式を、領域I,領域IIでそれぞれ求めよ。
  2. それぞれの領域での位相速度と群速度を求め、ωを使わずに表せ。
  3. 双方の領域で振動がつながるためには、角振動数ωは等しくなる。 kは、領域Iから領域IIに移動した時に増加したか、それとも減少したか？
  4. 領域Iから領域IIへ入ったとき、位相速度と群速度は増加したか、減少し たか。計算によって示し、その物理的解釈を述べよ。
解答例へ


[問い6]
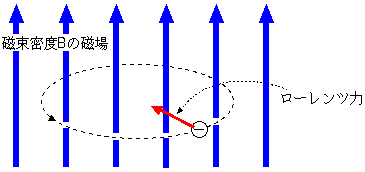磁場中の円運動
磁束密度Bの一様な磁場中で、電子（質量m、電荷−e）が磁場と垂直な平面内で半径rの等速円運動している。電子には速度とも磁場とも垂直な方向にevBの力（ローレンツ力）を受けながら運動する。
  1. 電子が速さvで等速円運動をしていると考えて、古典的運動方程式を書け。
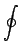  2. この運動は周期運動であるから、ゾンマーフェルトの量子条件周回積分pdq=nh を適用することができる(nは自然数)。この場合の量子条件はどのように書けるか。
  3. 電子を物質波と考えると、前問と同じ条件が導かれることを示せ。
  4. 電子の持つ運動エネルギーをnおよび定数(m,e,B,h)を使って表せ。
  5. この運動における∆xと∆pに関して考察し、不確定性関係が成立していることを示せ。
解答例へ


[問い7] 下のグラフのような波動関数を考える。虚数部分はなかったとする。
M字型波動関数
  1. 規格化せよ。
  2. 確率密度を計算せよ。
  3. xの期待値を計算せよ。
  4. この波動関数に虚数部を加えて、確率密度が−a < x < aの範囲で一定になるようにしたい。x < −a,x > aの範囲では確率密度０であったとする。虚数部として適当な関数の例を求めよ。
[解答例]
  1. ψ(x)は−a < x < 0ではψ(x)=−H/axであり、0 < x < aではψ(x)=H/axである。絶対値の自乗を積分すると、

    		∫ a

    −a 
    		H2
    a2
    		 x2 dx = H2
    a2
    		[
    		 1
    3
    		 x3]
    		 a

    −a 
    		 = 2H2
    3a2
    		 a3= 2H2 a
    3
    よって、H=√{[3/2a]}とすれば規格化される。
  2. ψの絶対値の自乗をとるので、−a < x < aにおいて、[3/(2a3)]x2。
  3. 対称性より0。
  4. 虚数部分の絶対値の自乗が定数−[3/(2a3)]x2であればよい。たとえば定数を[3/(2a3)]とすれば（絶対値の自乗が負にならない限り、どうおいてもかまわない）、虚数部の絶対値の自乗が[3/(2a3)](1−x2)となるので、虚数部は i√{[3/(2a3)]}√[(1−x2)]となる。




File translated from TEX by TTHgold, version 3.63.
On 7 Aug 2005, 14:00.