相対論講義録2005年第３回

←第２回へ　「相対論」講義録の目次に戻る　第４回へ→


2.4  「慣性系」の定義

　以上でわかるように、ニュートンの運動方程式はガリレイ変換によって不変である。しかし例えば座標系原点を等加速度運動させたりすると、もはや新しい座標系では運動方程式が成立しなくなる。
　そこで、ニュートンの運動方程式が成立する座標系を特別に「慣性系」と呼ぶ。ニュートンの運動方程式は上の座標変換で不変である。つまり、上の座標変換は、慣性系を別の慣性系に移すような座標変換である、ということが言える。
　たとえば地球表面に固定した座標系は厳密には慣性系ではない。地球の回転によって、コリオリ力および遠心力というみかけの力が働く。また、慣性系xに対して加速度運動しているような座標系
x′=x − 1
2
 at2
(2.7)
を導入したとすると、このx′系での運動方程式は
m(
 d2 x′
dt2
 +a) =F
(2.8)
あるいは
m d2 x′
dt2
 = F−ma
(2.9)
となってしまう。つまりx′系は慣性系ではなく、運動方程式の力の部分に余分な項−maが つく。この項は「慣性力」と呼ばれる。加速している物体（発進する車など）の上の観測者が加速と逆向きに力が働いているように感じるのが、この慣性力の もっとも単純な例である。このような加速度のある座標系は特殊相対論ではあまり扱われないが、一般相対論では非常に重要になる。



[問い2-2] 今、遊園地にあるフリーフォールの中での運動を考える。外から見ると、物体には重力が働くので、運動方程式は
m d2 y
dt2
 =−mg
(2.10)
である（yは上向きを正としてとった鉛直方向の座標）。フリーフォールも加速度gで自由落下運動しているとして、フリーフォールが静止しているような座標系を設定し、その座標系で立てた運動方程式には重力の影響がないことを示せ。



↑この問題は宿題です。

　とりあえず慣性系でない座標系のことは横に置いておくとして、
ガリレイ変換によって移り変わるどの慣性系においても、同じ運動の法則が成立する。
という原理を「ガリレイの相対性原理」と呼ぶ。この法則の「運動の法則」の部分を電磁気学を含めた「物理法則」に書き換えたいというのが相対論の目標である。後で詳しく述べるが、その目標達成のために「ガリレイ変換」の部分も「ローレンツ変換」に書き換えられることになる。
ローレンツ変換によって移り変わるどの慣性系においても、同じ物理法則が成立する。
というのが「特殊相対性原理」である6。

2.5  絶対空間に対するマッハの批判

　ニュー トンはニュートン力学を構築する時、「絶対空間」すなわち物体が静止していることの基準となる空間を仮定した。つまり、「静止している」ということが定義 できるとしたのである。マッハはこれを批判し、「物体が静止しているかどうかを判定することはできない」と主張した。実際ニュートンの運動方程式はガリレ イ変換で不変なのだから（動きながら見ても物理法則は変らないのだから）運動を見ているだけではその物体が静止しているかどうかを判定することはできな い。観測者自身すら、止まっているのかどうかが判定できないからである。
　この「動いているかどうか判定できない」というのは等速直線運動の場合に限る。たとえば観測 者が回転運動をしていれば、遠心力を感じるので、遠心力があるか否かを実験することで「自分は回転しているのか」を判定することができる（数式上で言え ば、先の計算のθが時間の関数であれば、運動方程式は不変ではない）。つまり、「静止系か否か」は実験で判断できないが「慣性系か否か」は判断できる、と いうことになる。
　しかしマッハはこの考え方も批判していて「自分が静止していて宇宙全体が回転していたとして も遠心力が働くかもしれない」と述べている。たとえばバケツをぐるぐる回すと中の水面の中央がくぼむ。これは「バケツの回転による遠心力で水が外へ追いや られるから」と説明されるのが普通である。そして「バケツが回転している」と判断できることは絶対空間がある証拠であると考えられていた（これを「ニュー トンのバケツ」と呼ぶ）。しかし、バケツが静止していて宇宙全体が回転していたとしても同じことが起こるかもしれない、「そんなことは起こらない」という 根拠はどこにもないとマッハは言うのである。今のところ（？）、誰も宇宙全体を回転させるような実験はできないので、この真偽はもちろんわからない。マッ ハは「各々の物体がどのように運動するかは、まわりにある物体全体との相互作用によって決まるべきだ」という思想（マッハ原理と呼ばれる。アインシュタイ ンもこの原理の信奉者だった）を持っていたので、安易に絶対空間を導入することに批判的だったのである。
　マッハの批判から学ぶべきことは「観測されていないことを固定観念で「決まっている」と思い込んではいけない」ということである7。 ニュートンは実際には観測することができない「絶対空間」をあると仮定してニュートン力学を作った（実際にはこの仮定は必要ではない）。「絶対空間」が存 在することは人間の感覚にはなんとなく、合う。だが、感覚を信用することは危険である。「物体に働く力は、物体の速度に比例する」という、人間の感覚に合 うアリストテレスの理論が長い間信じられてきた（が間違っている）ということを思い出さなくてはいけない。


第３章 ２次元、３次元の座標変換

　前の章では１次元的な問題に関して運動方程式の座標変換を調べたが、この章では２次元、３次元空間の座標変換についてまとめておく。いずれ、４次元時空での座標変換を考える時のガイドラインになるからである。

　しばらく物理の話より数学の話が増えるが、第４章では電磁気学の話に戻っていくので、しばらく辛抱。相対論の計算では以下でやるような行列やテンソル計算が必要になる。この章はその練習。

3.1  ２次元の直線座標の間の変換

　一つ次元をあげて、２次元空間の場合で考えてみる。二つの空間座標をx,yとすると、x,yに対して別々の平行移動を行う座標変換
x′=x−a, y′=y−b
であるとか、それぞれ別の速度でガリレイ変換する座標変換
x′=x−vx t, y′=y−vy t
などがある。
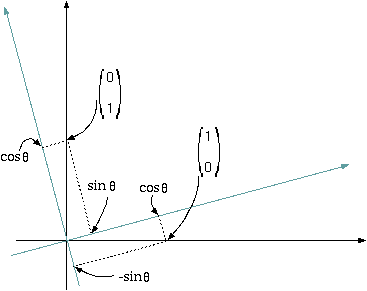
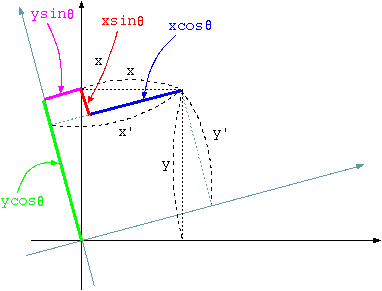
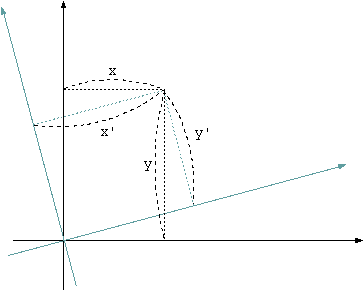回転の座標変換 　しかしここまでは１次元の話を重ねているだけで面白味がない。２次元ならではの座標変換は、右の図のような、座標軸の回転である。


x′=
xcosθ+ ysinθ
y′=
−xsinθ+ ycosθ

(3.1)



[問い3-1] 右の図に適当に補助線を引くことにより、(3.1)を図的に示せ。

　この問題は授業中にやった。右の図を参考にして考えればすぐにわかる。

問い3-1の参考図







(3.1)は、行列を使って

(
x′
y′
) =(
cosθ
sinθ
−sinθ
cosθ
)
(
x
y
)
(3.2)
と書くこともできる。

　ここで注意。行列なんか使わなくても、別に(3.1)でいいじゃないかと思う人もいるかもしれな い。しかし、(3.1)でもなんとかなりそうなのは２次元という単純な問題を考えているからである。問題が複雑になってくると行列を使った方が圧倒的に見 通しがよい。そうなる理由は、行列で書くと「演算」を表す部分
(
cosθ
sinθ
−sinθ
cosθ
)

と「演算されるもの」を表す部分

(
x
y
)


がきれいに分離することがあげられるだろう。

(x,y)=(1,0)という点と、(x,y)=(0,1)という点が(x′,y′)座標でみるとどう表せるかを考えよう。行列計算で書けば、

(
cosθ
−sinθ
) =(
cosθ
sinθ
−sinθ
cosθ
)
(
1
0
) ,    (
sinθ
cosθ
) =(
cosθ
sinθ
−sinθ
cosθ
)
(
0
1
)
(3.3)
となる。つまり行列
(
cosθ
sinθ
−sinθ
cosθ
)
は
(
1
0
) を座標変換した結果の (
cosθ
−sinθ
)
と、
(
0
1
) を座標変換した結果である (
sinθ
cosθ
)
を横に並べて作った行列であると考えることができる。 
(
1
0
)と(
0
1
)
は互いに直交し、それ自体の長さは１である。したがって、
(
cosθ
−sinθ
)と(
sinθ
cosθ
)
も互いに直交して長さは１である。長さや「直交する」という性質はどの座標系で見ても((x,y)座標系でも(x′,y′)座標系でも)同じだからである。
単位ベクトルを二つの座標系で見る。
　回転であるから当然であるが、この式は
(x′)2+(y′)2 = x2+y2
(3.4)
を満足する。つまり、原点からの距離（上の式は距離の自乗）はこの変換で保存する。 これを行列で考えよう。まず、

          
( x    y )

(
x
y
)
 = x2+y2
(3.5)
のように、行ベクトルと列ベクトルのかけ算という形で距離の自乗を表現する。列ベクトルの座標変換は(2)だったが、行ベクトルの座標変換は

          
( x′   y′)
=           
( x    y )


(
cosθ
−sinθ
sinθ
cosθ
)
 =           
( xcosθ+ ysinθ   −xsinθ+ ycosθ)

(3.6)
と書ける。(2)と場合とは行列の並び方が変わっているものになっていることに注意しよう（具体的に行列計算をしてみればこれで正しいことはすぐにわかる）。この、
A = (
a11
a12
a21
a22
) →At = (
a11
a21
a12
a22
)
(3.7)
のような並び替えを「転置(transpose)」と呼び、行列Aの転置はAtという記号で表す。転置はaij→ ajiと書くこともできる。aijとは「i番目の行の、j番目の列の成分」であるから、iとjを入れ替えるということは行番号と列番号を取り替えることである。ゆえに、転置を「行と列を入れ替える」とも表現する。
　この式を使って、(x′)2+(y′)2を計算すると、

          
( x′   y′)

(
x′
y′
) =           
( x    y )

(
cosθ
−sinθ
sinθ
cosθ
)
(
cosθ
sinθ
−sinθ
cosθ
)
(
x
y
)
(3.8)
となるが、

(
cosθ
−sinθ
sinθ
cosθ
)
(
cosθ
sinθ
−sinθ
cosθ
)
 =(
cos2θ+sin2θ
cosθsinθ−sinθcosθ
sinθcosθ−cosθsinθ
sin2θ+ cos2θ
)
 =(
1
0
0
1
)
(3.9)
となることを考えると、


( x′   y′)

(
x′
y′
) =
( x    y )
(
x
y
)
すなわち、(x′)2+(y′)2=x2+y2になることがわかる。このように必要な部分だけを計算できるのが行列計算のメリットの一つである。
(3.9)が成立することは、直接的計算でももちろんわかるのだが、ベクトルの意味を考えればその意味が明白に理解できる。
行列のかけ算
上の図のように、行列のかけ算というのは結局、行ベクトルと列ベクトルの内積の計算を繰り返すものである。そして、

(
cosθ
sinθ
−sinθ
cosθ
)
が「互いに直交して長さが１であるような二つのベクトルを横に並べたもの」であり、

(
cosθ
−sinθ
sinθ
cosθ
)
は同じベクトルを縦に二つ並べたものである。計算の結果１になるのは「自分自身との内積」すなわち「ベクトルの長さの自乗」を計算している部分で、０になる部分は「直交している」というところを計算している部分である。
今の一例に限らず、回転を表すような行列は「互いに直交して長さが１になるベクトルを並べたもの」という性質を持っていなくてはならない。
逆に、(3.4)を満足するような座標変換が

(
x′
y′
) = (
a11
a12
a21
a22
)(
x
y
)
(3.10)
と書けていたとすると、二つの列ベクトル
(
a11
a21
),(
a12
a22
)
は、どちらも長さが1で、互いに直交しなくてはいけない。このような条件を満たしている行列を直交行列といい、Aが直交行列であれば、AtAは単位行列となる。
　直交行列であれ、というだけの条件では回転の行列になるとは限らない。たとえば、
(
1
0
0
-1
)
は直交行列であるが、その物理的内容は回転ではなく、y軸の反転である。直交行列で、かつ行列式が１であるという条件を満たす場合、その行列は回転を表す。

　なお、量子力学で出てくるユニタリ変換（ユニタリ行列）というのは、この直交変換（直交行列）の、複素数バージョン。やはり座標系（ただし複素数の）を複素数的に回転させる。
[問い3-2] 行列
(
cosθ
sinθ
sinθ
−cosθ
)
はどんな座標変換を表す行列か。図で表現せよ。
[問い3-3] 直交行列の行列式は1か−1か、どちらかであることを以下を使って示せ。
  1. 二つの行列(A,B)の積(AB)の行列式(det(AB))は、それぞれの行列式の積(detAdetB)である。
  2. 転置しても行列式は変わらない(detA = det(At))。
 二つの行列(A,B)の積(AB)の行列式(det(A))」となっていたのは誤り。上のように訂正。
[問い3-4] 今考えた直交行列Aの行列式detAには、どのような幾何学的意味があるか。その意味を考えて、detAが1または−1であることの意味を説明せよ。
ヒント:行列式detA = a11a22−a12a21は、ベクトル
(
a11
a21
)と(
a12
a22
)
の何？？？


↑この問題は宿題です。

学生の質問・コメントから

　マッハの原理の「相互作用によって決まる」とはどういう意味でしょうか。等速運動する電車の中でジャンプする人の運動も、この考えで理解できるんでしょうか。
　物体が動いているのか動いていないのか、あるいは加速しているのかしていないのかは、すべてまわ りの物体と比較してどんな運動をしているかで決まるべきだ、というのがマッハの原理です。等速度運動の場合ではあまり関係ありません。通常のニュートン力 学では等速運動の場合で電車が動くのか、宇宙全体が逆向きに動くのかわからない、と考えます。マッハの原理では、たとえば電車が加速するのか、宇宙全体が 逆向きに加速したのか、それもわからないと主張します。つまり「等速運動する電車でのジャンプ」の話より、もっと深い話になってます。

　２次元の座標変換はイメージできましたが、３次元や４次元はこんなふうにイメージできないんですか？
　できます。ちょっと苦労するし、図を書くのがたいへんですが。

　註の、一般座標変換の意味がわかりません。すべての座標系ってのは慣性系とは違うのですか？
　慣性系じゃない座標系も含めて、ありとあらゆる座標系の間の座標変換をしても物理法則は変わらないんだ、というのが一般相対性原理です。つまり、範囲が特殊相対性原理に比べて、かなり広くなってます。

　直交行列は座標を回転させる行列なのですか？
　回転＋反転ですね。

　ガリレイ変換をせっかく習ったのにだめだと言われてショックだった。（同様のコメント多数）
　すぐにもっと役に立つローレンツ変換を習います。

　地球上は近似的な慣性系だそうですが、厳密な慣性系は存在するのですか？
　存在します。つまりは加速度運動してないような座標系を作ればいいのですから。ただし、一般相対論を習うと、「重力が働いているところは慣性系ではない」という驚愕の事実が判明するので、そこまで考えると厳密な慣性系は無重力状態でないと実現しないことになります。

　行列って役に立つんですねぇ、初めて知りました（同様のコメント多数）
　そうなんです。役に立つから高校数学で教えているのです。

　いつまでたっても行列は嫌いです（これも複数から）
　でもねぇ、やっぱりあった方が便利なんですよ。

Footnotes:

6さらに「一般座標変換によって移り変わるすべての座標系のおいてすべての物理法則が成立する」となると「一般相対性原理」。これを実現するのが一般相対論。
7このあたりの「心」は量子力学にもつながるかもしれない。ただし、マッハ自身は量子力学どころか、分子論に対しても批判的であった。つまりは全てを疑ってかかる人だったのだろう。

←第２回へ　「相対論」講義録の目次に戻る　第４回へ→
File translated from TEX by TTHgold, version 3.63.
On 10 May 2005, 12:41.