 第1章
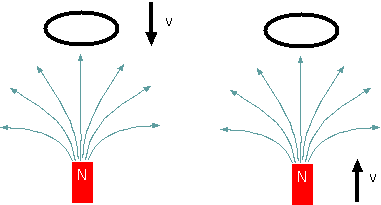
で概要だけ述べた、電磁誘導に関する疑問について、ここでくわしく考えておこう。図のように、二つの現象を考える。左の図では、コイルが磁石に近づき、右
の図では、磁石がコイルに近づく。二つの現象は、見る立場を変えれば同じ現象であり、結果として「コイルに時計まわりの電流が流れる」という点でも同じで
ある。しかし、その記述は同じではない。
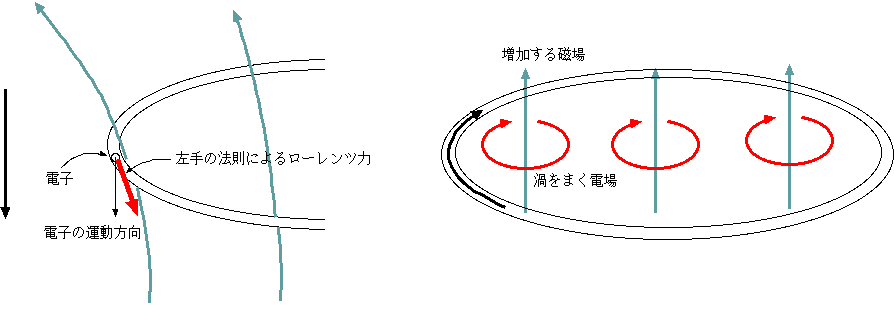
右図の場合であれば、それはコイル内の磁束密度が時間変化するということからくると解釈される。すなわちMaxwell方程式のrot→E = −[(∂→B)/(∂t)] にしたがって、磁束密度が変化している場所には電場の渦が発生していて、その電場によってコイル中の電子が力を受け、電流となる。よく知られているように、この時に発生する電位差は、ファラデーの電磁誘導の法則V=−[(dΦ)/(dt)]によって求められる。ここでΦは回路内をつらぬく磁束であり、Vの符号はΦに対して右ネジの向きに電流を流そうとする時にプラスと定義される。
第1章
で概要だけ述べた、電磁誘導に関する疑問について、ここでくわしく考えておこう。図のように、二つの現象を考える。左の図では、コイルが磁石に近づき、右
の図では、磁石がコイルに近づく。二つの現象は、見る立場を変えれば同じ現象であり、結果として「コイルに時計まわりの電流が流れる」という点でも同じで
ある。しかし、その記述は同じではない。
右図の場合であれば、それはコイル内の磁束密度が時間変化するということからくると解釈される。すなわちMaxwell方程式のrot→E = −[(∂→B)/(∂t)] にしたがって、磁束密度が変化している場所には電場の渦が発生していて、その電場によってコイル中の電子が力を受け、電流となる。よく知られているように、この時に発生する電位差は、ファラデーの電磁誘導の法則V=−[(dΦ)/(dt)]によって求められる。ここでΦは回路内をつらぬく磁束であり、Vの符号はΦに対して右ネジの向きに電流を流そうとする時にプラスと定義される。
|

|
| (4.5) |
| (4.6) |
| (4.7) |
| (4.6') |
|
∂x1 ∂x′i |
|
|
∂ ∂x1 |
|
|
| (4.7') |
| (4.7'') |
|
| (4.8) |
| (4.9) |
| (4.10) |
| (4.11) |
| (4.12) |
| (4.13) |
| (4.14) |
| (4.15) |
| (4.16) |
| (4.17) |
|
|
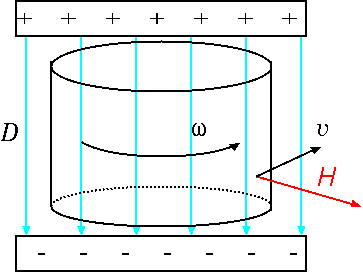 ヘルツの方程式が正しいかどうかを判定できる実験として、レントゲン(Röntgen)とアイフェンヴァルト(Eichenward)による、回転する誘電体の実験がある。図のように誘電体を半径Rの円筒形にして、軸方向に磁場をかけておいて回転させる。
エーテルがこの回転する誘電体と一緒に運動しているとすれば、ヘルツの方程式の中の→vには、各点各点の回転速度を代入すればよい(これで本当にいいのかは再考が必要)。磁場が一定だとしてヘルツの方程式(4.14)はこの場合、
ヘルツの方程式が正しいかどうかを判定できる実験として、レントゲン(Röntgen)とアイフェンヴァルト(Eichenward)による、回転する誘電体の実験がある。図のように誘電体を半径Rの円筒形にして、軸方向に磁場をかけておいて回転させる。
エーテルがこの回転する誘電体と一緒に運動しているとすれば、ヘルツの方程式の中の→vには、各点各点の回転速度を代入すればよい(これで本当にいいのかは再考が必要)。磁場が一定だとしてヘルツの方程式(4.14)はこの場合、
| (4.18) |
| (4.19) |
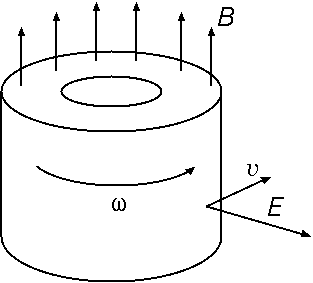 上で電場中で物体を回転させて磁場を作ったことの逆で、物体を磁場中で回転させて分極を作る実
験がある。この現象については、アインシュタインとラウプがローレンツ変換を使って磁場中で動く磁性体の分極を計算している(1908年)。W.ウィルソ
ンとH.A.ウィルソンが実験で確認した(1913年)。この実験結果も、素朴にヘルツの方程式を適用した計算とは合わないが、相対論的計算ならば合う。
ここでは「誘電体が回転している速度をヘルツの方程式の→vに
代入する」という計算をやっているが、物体が動いてもその場所のエーテルは動かないのかもしれない。実は「物体が動くとその周りのエーテルは一緒に動くの
か?」ということを定めるための実験は、すでに1851年にフィゾー(Fizeau)によってなされている。彼は水中の光速度が、水が流れている時にはど
のように変化するかを間接的に測定19し、静止している水中の光速をuとすると、光の進む方向に水が速さvで流れているときは
上で電場中で物体を回転させて磁場を作ったことの逆で、物体を磁場中で回転させて分極を作る実
験がある。この現象については、アインシュタインとラウプがローレンツ変換を使って磁場中で動く磁性体の分極を計算している(1908年)。W.ウィルソ
ンとH.A.ウィルソンが実験で確認した(1913年)。この実験結果も、素朴にヘルツの方程式を適用した計算とは合わないが、相対論的計算ならば合う。
ここでは「誘電体が回転している速度をヘルツの方程式の→vに
代入する」という計算をやっているが、物体が動いてもその場所のエーテルは動かないのかもしれない。実は「物体が動くとその周りのエーテルは一緒に動くの
か?」ということを定めるための実験は、すでに1851年にフィゾー(Fizeau)によってなされている。彼は水中の光速度が、水が流れている時にはど
のように変化するかを間接的に測定19し、静止している水中の光速をuとすると、光の進む方向に水が速さvで流れているときは
| (4.20) |
|