相対論講義録2005年第９回

　←第８回へ　「相対論」講義録の目次に戻る　第10回へ→

　前回、前々回でローレンツ変換をグラフと図で解説した。もう少し物理的内容を詰めてから、もう一 度数式での導出をやるつもりだったが、どうも今ひとつうまく伝わってない感じがしたので、数式での導出を先にやることにした。そのため、６章の残りと７章 を飛ばして８章に行った（後で戻る予定）。

第８章　ローレンツ変換と４次元時空

8.1  ローレンツ変換の数式による導出

この章ではローレンツ変換に関してグラフで行った議論を数式でもう一度まとめ、その物理的および幾何学的内容について考えていく。
まず、ローレンツ変換を計算により求めよう。ローレンツ変換が満たすべき条件として、次の３つを取る。
  1. この変換によって、古い座標系での光円錐( (x−x0)2+(y−y0)2+(z−z0)2−c2(t−t0)2=0 )は新しい座標系でも光円錐((x′−x′0)2+(y′−y′0)2+(z′−z′0)2 −c2 (t′−t′0)2=0)へと移る(光速度不変の原理)。
  2. この座標変換において特別な点はない(一様性)。
  3. この座標変換において特別な方向はない(等方性)。
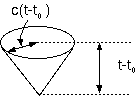光円錐 　1.が主張しているのは、光速度不変の原理を満足せよ、ということである。ある時空点(t0,x0,y0,z0) （x′座標系では(t′0,x′0,y′0,z′0)）から光が出て、時空点(t,x,y,z) （x′座標系では(t′,x′,y′,z′)）にたどりついたとする。時刻t（あるいは時刻t′）には、その光はc(t−t0) （あるいはc(t′−t′0)）広がっている。ゆえに(x−x0)2+(y−y0)2+(z−z0)2−c2(t−t0)2=0が成立するならば、(x′−x′0)2+(y′−y′0)2+(z′−z′0)2 −c2 (t′−t′0)2=0も成立せねばならない。光速度はどっちの座標系でもcだからである。くどいようだがもう一度書く。これは実験事実である。また、ここで光速度一定という現象に着目してはいるが、これは光を特別視しているわけではなく、マックスウェル方程式が生み出す物理現象の代表として光を使っているということに注意して欲しい。「光速度一定」は「どの座標系でも成立すべき物理法則」の代表なのである29。

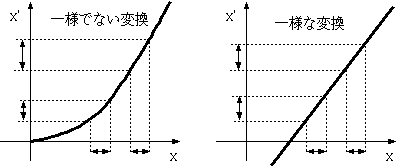非一様な変換と一様な変換　2.が主張しているのは、この変換が一様であれ、ということである。
　たとえばx′ = ax2のような変換をしたとすると、x=0付近と、そこから遠い場所では、xが変化した時のx′の変化量が違う。これはつまり、x座標系で測った1メートルが、x′ 座標系では場所によって10センチになったり3メートルになったりと、違う長さになるということである。しかし今考えているのは座標系の一様な運動である から、こんなことは起こらないだろう(ある座標系での1メートルが別の座標系では等しく50センチになることはあり得るとしても！)。この条件を満たすた めには、(x,y,z,ct)と(x′,y′,z′,ct′)が一次変換で結ばれなくてはならない。
　3.が主張しているのは、たとえばこういうことである。x 軸の正方向へ速さvで運動している場合と、x軸の負方向へ速さvで運動している場合を比べたとする。この二つは、最初にx軸をどの方向にとったかというだけの違いであって、物理の本質的な部分は違わないはずである。つまり、ある方向へ移動する座標系だけが特別扱いされるようなことはあってはならない。
　以下で、これらの要請だけからガリレイ変換に替わる新しい座標変換を導く。
　x′系の空間的原点x′=y′=z′=0が、x座標系で見ると速度vでx軸方向に移動していて、時刻t=0では原点が一致しているとする。このことから、x′=0 という式を解くと、x=βctという答えが出るようになっていることがわかる。この条件はガリレイ変換x′=x−vtでも成立する。2.の条件があるので、
x′=A(x−βct)
(8.1)
という形でなくてはならないことがわかる。y方向、z方向には座標軸は移動していない。つまりこの座標変換で、y=0である場所はy′=0である場所に移る。zに関しても同様なので、
y′=By,   z′=Bz
(8.2)
となるべきだろう。ここで、簡単のためにy軸やz軸の方向も変わらないとした。この二つの式の係数がどちらもBなのは、空間の対称性から判断した。
　しかし、要請3.から、Bは1でなくてはならないことがわかる。Bが1でなかったとすると、この座標変換によってy軸やz軸方向の長さが伸びたり（B > 1 の場合）、縮んだり（B < 1の場合）することになる。運動方向を反転(v→ −v)したとしよう。この時の変換は元の変換の逆変換であろうから、y"=y/B,    z"=z/Bという形になる。つまり+x方向ではB 倍になったとしたら、−x方向では1/B倍でなくてはならない。B ≠ 1だと、この現象は要請3.に反する。
　 時間座標に関しては、
ct′ = C(ct−D x−E y−F z)
(8.3)
と置いてみる。

　ここで -Ey -Fz も入れておいたが、どうせE=F=0なので、最初から ct′ = C(ct−D x) にして計算した方がよかった。来年から省こう。
　以上の座標変換に対して、要請1.すなわち「x2+y2+z2−c2 t2=0の時に(x′)2+(y′)2+(z′)2−c2(t′)2=0になれ」という条件（書き忘れているが、簡単のためx0など0の着く量は全部０にした）が成立するためにはA,C,D,E,Fがどうならなくてはいけないかを考える。そのためにまず (x′)2+(y′)2+(z′)2−(ct′)2を計算しよう。

　このあたりの式、テキストはいくつか間違っていたので、赤字で訂正してあります。
(x′)2+(y′)2+(z′)2−(ct′)2 =
A2(x−βct)2 + y2 +z2 −C2(ct−D x −E y −F z)2
=
(A2−C2 D2)x2+(1-C2E2)y2 +(1-C2F2)z2 +(A2 β2 − C2)(ct)2

−(2A2β− 2C2 D) xct+2 C2 E y ct +2C2 F z ct

+…(y,zの1次、2次を含む項)

(8.4)
　ここで、条件x2+y2+z2−c2t2=0であることを思い起こす。よってここではx,y,zが独立な変数であって、ctはct=±√[(x2+y2+z2)]であるとして扱う。x,y,zは各々独立に動かせるから、xct,yct,zctの係数は零でないと困る。これから、E=F=0とA2β− C2D=0がわかる。そこでD = [(A2β)/(C2)]と代入して、

0=
(A2− A4 β2
C2
 )x2+y2 +z2 +(A2β2 − C2)(ct)2
0=
(A2− A4 β2
C2
 )x2+y2 +z2 +(A2β2 − C2)(x2+y2+z2)
0=

( A2− A4 β2
C2
 +A2β2 − C2) x2+(1+A2β2 − C2)y2 +(1 +A2β2 − C2) z2

(8.5)
ここでx2の係数は0にならなくてはいけないが、

A2−A4 β2 C2+A2β2 − C2 =
0
A2−C2 − A2 β2
C2
 (A2−C2) =
0
(A2−C2)( 1 − A2 β2
C2
) =
0

(8.6)
となるから、A2=C2か、[(A2 β2)/(C2)]=1かが成立せねばならない。しかし[(A2β2)/(C2)]=1だと、y2の前の係数が1になってしまい、けっして0にならない。そこで、C2=A2として、
1 = C2(1−β2)
(8.7)
という式が成立する。これで座標変換は
x′ = 1


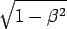sqrt(1-β^2)
 (x−βct), y′ = y, z′=z, ct′ = 1


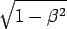sqrt(1-β^2)
 (ct−βx)
(8.8)
とまとめられる。当然ながら、図から求めたものと一致する。あらためて指摘しておくと、係数sqrt(1-β^2)は、xやtのスケールの変化（ローレンツ短縮やウラシマ効果）を表している。また、ct′の式にct−βxが現れることは、tの同時刻とt′の同時刻が場所によって変化すること(t=一定とt′=一定がグラフ上で平行線ではない)を示しているのである。
なお、ここまでの計算では簡単のために運動方向をx方向に限ったし、y,z座標に関しても同じ方向を向いているとした。一般的には運動方向が任意の方向を向いたものや、これに座標軸の回転が組み合わさったものが出てくる可能性がある。


　補足。上のローレンツ変換で、βが通常１よりずっと小さいことを思い出せば、sqrt(1-β^2)は１だと思ってもさしつかえない。また最後のct-βxのところも、βxは忘れてよい。x-βctのβctは、後ろからcがかかっているので忘れてはだめ。と考えると、βが小さい状況では、
x′ = x−βct, y′ = y, z′=z, ct′ = ct

という式になるわけだが、これはガリレイ変換そのものである。つまり、我々の日常の経験では、ガリレイ変換はじゅうぶんよい近似として成立しているのである。

　ここまでやったところで6.3節に戻った。

6.3  （新しい意味の）ローレンツ短縮

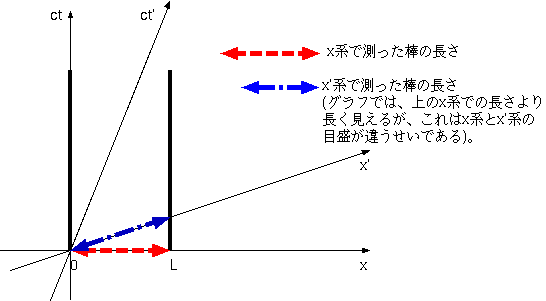ローレンツ短縮の図　ローレンツがad hocに導いたローレンツ短縮と似た現象が、この座標変換でも導かれることを示そう。今、一つの棒をx−t座標系で見て静止するように置いたとする。棒の長さをLとして、一方の端をx=0、もう一方の端をx=Lに置いたとする。時間tが経過してもこのxの値は変化しない。では、これをx′ 座標系で見るとどうか。棒の一方の端の時空座標を(x1,t1)または(x′1,t′1)で、もう一方の端の時空座標を(x2,t2)または(x′2,t′2)で表すとすれば、

(x1,t1)=(0,t)
↔
(x′1,t′1)=(−γβct,γt)

(6.12)

(x2,t2)=(L,t)
↔
(x′2,t′2)=(γ(L−βct),γ(t−[β/c]L))

(6.13)
となる。
　この当たりの式も、一部/cが落ちてました。上のように訂正してください。
　ここでx′座標系で棒の長さを測るとしよう。「x′座標系での棒の長さ」はt′1=t′2にした時のx′2−x′1で計算される。上の表の(x′1,t′1)と(x′2,t′2)では、t′1 ≠ t′2なので、t2の方の時間をt→ t+[β/c]Lとずらして、
(x2,t2)=(L,t+ β
c
 L)↔ (x′2,t′2)=(γ(L−βct−β2 L),γt)
とすれば、t′1=t′2になる。この時のx′2−x′1を計算すると、
x′2 − x′1 = γ(L−β2L) = L 1−β2


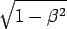sqrt(1-β^2)
 =L
sqrt(1-β^2)
 
(6.14)
となり、x系での長さLに比べ、sqrt(1-β^2)倍になっている（縮んでいる）ことがわかる。
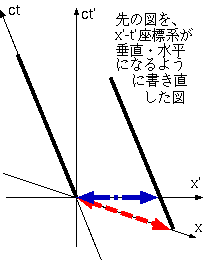立場を変えてみたローレンツ短縮の図
　この式は形としてはローレンツがマイケルソン・モーレーの実験結果を説明するために導入した短縮と同じである。逆に言うと「ローレンツ短縮が起こるべし」という要請から、係数Aを 決めることも可能であったことになる。しかし、今求めた新しい意味のローレンツ短縮と、古い意味のローレンツ短縮は根本的に意味が違う。まず、ローレンツ はエーテルとの相対運動が理由で機械的に短縮が起こると考えたが、ここでの短縮は座標変換によって生じたものであって、力が働いて起こる短縮とは全く意味 が違う。また、図で説明してあるように、座標系が違うことによって「同時刻で空間的に離れた２点」という２点の定義の仕方そのものが変わってくる。ガリレ イ変換ではこんなことは生じない。古い意味のローレンツ短縮はガリレイ変換を使った物理の中で考えられたものだから、同様に「座標系が違えば同時刻が違 う」ということを考慮せずに単に短縮すると仮定している。
　何よりここで導かれた短縮は光速度不変の原理と特殊相対性原理から自動的に導出されたもので、筋道だった説明が与えられていることが大きな違いである。



[問い6-2] ミュー粒子と呼ばれる粒子は、2×10−6秒で崩壊してしまう。ウラシマ 効果を考えないと、たとえ光の速さ(3×108m/s)で走ったとしても、 6×102mしか走れない。しかし、大気圏の上の方で発生したミュー粒子 が、ちゃんと地上に到着する。これは、光速の99％近くで走っているおかげで時 間の進み方が遅くなっているからであると考えることができる。
これをミュー粒子の立場に立って（つまり、ミュー粒子と一緒に動く座標系で） 考えるとどうなるだろうか。この立場では、ミュー粒子は静止している（動いて いるのは地球の方）ので、2×10−6秒で崩壊してしまうはずである。で はなぜ、大気圏の下まで到着することができるのか？？

(ヒント：動いているのは地球の方。当然、大気圏も動く！）

 [問い6-3]
  1. 二台の電車AとBのすれちがいをある人（観測者O）が見ている。Oから見る と、AとBはx軸の正方向と負方向にそれぞれ速さvで走ってくるように見 える。電車の固有長さ（すなわち、電車が静止している系で測定した長さ）はと もに2Lであるとする。観測者の座標系で時刻t=0において、x=0の場所でA、 Bの中央が一致していたとする。これらの電車の運動を表すグラフを書け。
  2. 電車Aの中央に乗っている観測者をα、電車Bの中央に乗っている観測者 をβとする。α、β、Oの３人の世界線は、さっきのグラフの原点で重な る。αは「電車Bの方が電車Aより短い」と観測し、βは「電車Bの方が電 車Aより短い」と観測する（互いに相手を「自分より短い」と判断する）。 先の問題のグラフに「αが原点にいる時に観測する電車A,Bの長さ」と 「βが原点にいる時に観測する電車A,Bの長さ」を書き込み、互いに相手 を短いと観測することを説明せよ。




学生の感想・コメントから

　数式で出した方がわかりやすい。
　という人と、
　やはり図で説明してくれた方がすっと頭に入ってくる。数式で説明されるとだまされたみたい。
という人と、２種類いるみたいです（どっちでもわからないって人を入れると３種類）。できれば両方でしっかりわかって欲しい。

　ローレンツ変換にはガリレイ変換がちゃんと入っていて、うまくできているなぁと思った。
　ほんとに、うまくできています。

　「x2+y2+z2−c2 t2=0の時に(x′)2+(y′)2+(z′)2−c2(t′)2=0になれ」という条件は、「どの座標系でも固有時間は同じである」という条件と同じですか？
　同じではありません。後者が成立すれば前者が成立します。しかし前者が成立しても後者が成立するとは限りません。後者⇒前者なのです。ただし、今考えているローレンツ変換では両方が成立します。これは要請2.と要請3.が組み合わされているおかげです。

　t→ t+[β/c]Lとずらす理由は何ですか？
　そうすれば、t'が同じになります。今観測者はx'-ct'座標系にいるので、彼の同時（つまり、t'が等しい）状態で棒の先端と後端の位置を測定して、棒の長さを決めます。そのためにはtで見ると同時でない状態に持って行かなくてはいけないのです。

　ローレンツ短縮ですが、「動いている棒を止まっている人が見た時」と「止まっている棒を動いている人が見た時」はどちらも棒が縮んで見えるのですか？
　はいその通り。この二つは相対的に同じですから、同じ見ためになります。どうしてそうなるのかは、図を見ながら考えてみてください。

Footnotes:

29こうやって作ったローレンツ変換がマックスウェル方程式を不変に保つかどうかはちゃんとチェックする必要がある。答を先に書いておくと、電場や磁場のローレンツ変換をちゃんと定義すれば不変になっている。
 
File translated from TEX by TTHgold, version 3.63.
On 21 Jun 2005, 12:48.