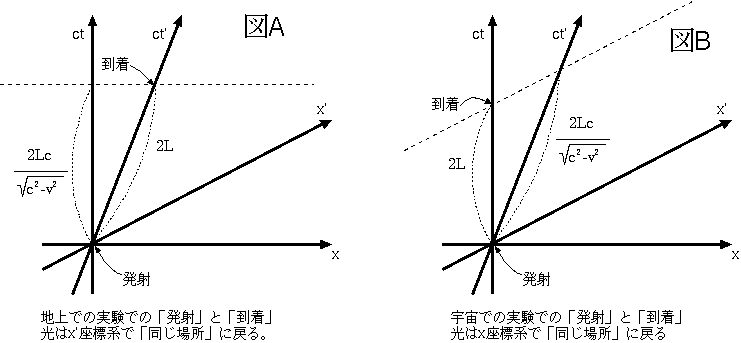
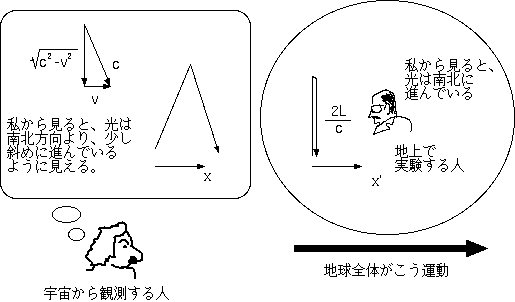
 マイケルソンとモーレーの実験における、南北方向の光について思い出す。実験装置が動いていないという立場(地上にいる人の立場)で観測すると、距離2L を光が進むので、往復に[(2L)/(c)]かかる。一方同じ現象を、装置が速さv で東に動いているという立場(地球外の人の立場)で観測する。この人にとっては光は南北方向にではなく、少し斜めに(光の速度ベクトルcと地球の速度ベクトルvが図に書いたような関係になるように)進んでいる。この人にとっての光の速度の南北方向成分は
マイケルソンとモーレーの実験における、南北方向の光について思い出す。実験装置が動いていないという立場(地上にいる人の立場)で観測すると、距離2L を光が進むので、往復に[(2L)/(c)]かかる。一方同じ現象を、装置が速さv で東に動いているという立場(地球外の人の立場)で観測する。この人にとっては光は南北方向にではなく、少し斜めに(光の速度ベクトルcと地球の速度ベクトルvが図に書いたような関係になるように)進んでいる。この人にとっての光の速度の南北方向成分は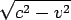 になる(当然cより遅い)。
ゆえにこの時に光が発射されてから到着するまでの時間は[(2L)/
になる(当然cより遅い)。
ゆえにこの時に光が発射されてから到着するまでの時間は[(2L)/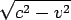 ]となる(Lは南北方向の距離であることに注意せよ)。つまり、地球外の人の方が同じ現象にかかった時間を
]となる(Lは南北方向の距離であることに注意せよ)。つまり、地球外の人の方が同じ現象にかかった時間を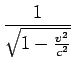 倍だけ、長く感じることになる。
このように、動いている人(この場合は地球上にいる人)の時間は止まっている人(この場合は宇宙から観測する人)の時間より遅くなることになる。これを浦島太郎の昔話になぞらえて、ウラシマ効果と呼ぶ。
倍だけ、長く感じることになる。
このように、動いている人(この場合は地球上にいる人)の時間は止まっている人(この場合は宇宙から観測する人)の時間より遅くなることになる。これを浦島太郎の昔話になぞらえて、ウラシマ効果と呼ぶ。| 地上の座標系 | 宇宙船の座標系 | |
| 発射 | x′=0, t′=0 | x=0,t=0 |
| 到着 | x′=0, t′=[(2L)/(c)] | x = A′v×[(2L)/(c)], t=A′×[(2L)/(c)] |
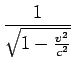 倍長いのだから、
[(2L)/(c)]×
倍長いのだから、
[(2L)/(c)]×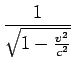 =A′×[(2L)/(c)]となって、ゆえにA′=
=A′×[(2L)/(c)]となって、ゆえにA′=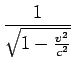 ということになる。
ということになる。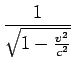 とわかる。
ここで、地上でも宇宙でも相手の方が時間が遅いと感じるなんておかしい、と思うかもしれないが、次のように考えるとおかしなところは何もない。
とわかる。
ここで、地上でも宇宙でも相手の方が時間が遅いと感じるなんておかしい、と思うかもしれないが、次のように考えるとおかしなところは何もない。

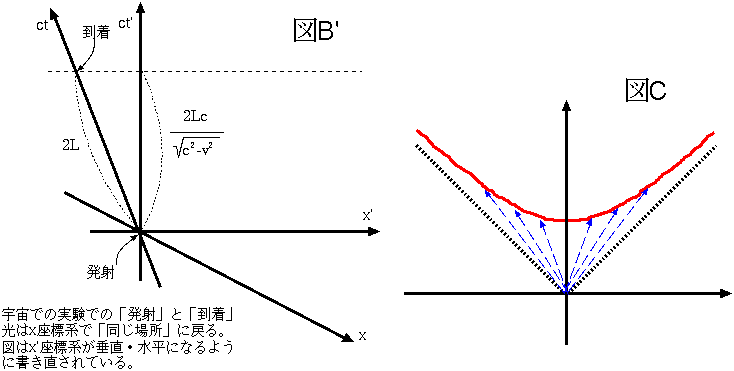 図B'は、図Bを、x′−t′座標系が垂直になるように書き直したものである。ct 軸に関しては図Bを左右逆転したような図になっている(速度逆向きの座標変換だから)。
また、図C中の点線は原点からいろんな速度で出発した人の時計が同じ時刻を刻む時空点を線でつないだものである。速く動く人ほど持っている時計は遅く進むので、垂直に対して傾いた軌道をとっている人ほど、止まっている人との時間差が大きくなる。
結局、x′−t′系での同時がx−t座標系から見ると傾いていてx−t座標系での同時と同じではないため、このように「互いに相手の時間を短く感じる」という一見矛盾した結果が出る。
図B'は、図Bを、x′−t′座標系が垂直になるように書き直したものである。ct 軸に関しては図Bを左右逆転したような図になっている(速度逆向きの座標変換だから)。
また、図C中の点線は原点からいろんな速度で出発した人の時計が同じ時刻を刻む時空点を線でつないだものである。速く動く人ほど持っている時計は遅く進むので、垂直に対して傾いた軌道をとっている人ほど、止まっている人との時間差が大きくなる。
結局、x′−t′系での同時がx−t座標系から見ると傾いていてx−t座標系での同時と同じではないため、このように「互いに相手の時間を短く感じる」という一見矛盾した結果が出る。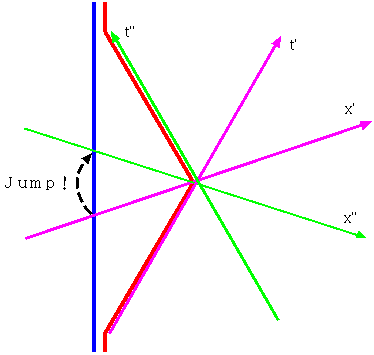 ロケットが地球に帰ってきたら、どっちの時計が進んでいることになるんですか?
ロケットが地球に帰ってきたら、どっちの時計が進んでいることになるんですか?
|
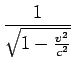 という座標変換をすれば、どの座標系でも光速は一定値cを取ることがわかった。
という座標変換をすれば、どの座標系でも光速は一定値cを取ることがわかった。
|
| (6.11) |
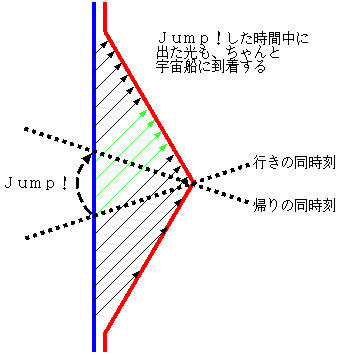 宇宙船が折り返した時、座標が変わり、急に時間が経つとき、宇宙船からはその間に地球上で起こったことは確認できないんですか?
宇宙船が折り返した時、座標が変わり、急に時間が経つとき、宇宙船からはその間に地球上で起こったことは確認できないんですか?