
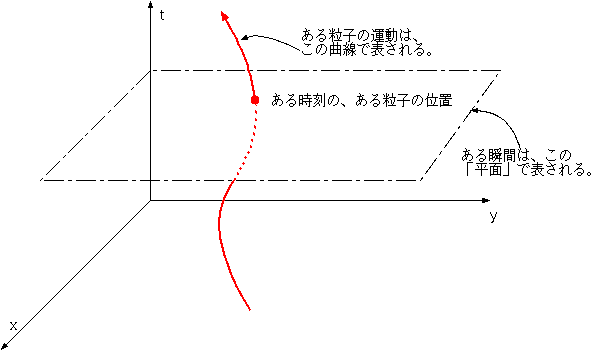
 相対論では、4次元、すなわち4つの座標を
使って運動を記述するということが大事になる。「次元」という言葉はずいぶんいろんな意味に使われていて9、一般社会においては「4次元」という言葉は特に謎めいたイメージを持たされて
いる。しかしここで言う「次元」というのは「いくつの数を指定すれば系の状態が決まるか」という意味であって、それが「4」であるということは、別に不思
議なことではない。例えば待ち合わせをする時、「じゃあ、生協食堂前で会おう」では待ち合わせはできない。かならず「何時に」ということも決めるはずであ
る。「生協食堂前」を指定するのに数字を使うとしたら、3つの数字が必要である10。これに時刻を足して4つの数字を指定して始めて待ち合わせが成立する。つま
りこの場合必要な数字は4つ。これを「4次元」と言う11。
物体の位置だけを問うのなら、3次元でいい。ニュートン力学の世界では、3次元空間と1次元の時間は完全に切り放されて、別個に存在している。相対論的
世界では、空間と時間の間に少し関係が生じてくる。そのため、相対論の話をする時には4次元的記述が好まれる(と、今言ってもわからないだろうけどれど、
授業が進むにつれてわかってくるはずである)。
相対論では、4次元、すなわち4つの座標を
使って運動を記述するということが大事になる。「次元」という言葉はずいぶんいろんな意味に使われていて9、一般社会においては「4次元」という言葉は特に謎めいたイメージを持たされて
いる。しかしここで言う「次元」というのは「いくつの数を指定すれば系の状態が決まるか」という意味であって、それが「4」であるということは、別に不思
議なことではない。例えば待ち合わせをする時、「じゃあ、生協食堂前で会おう」では待ち合わせはできない。かならず「何時に」ということも決めるはずであ
る。「生協食堂前」を指定するのに数字を使うとしたら、3つの数字が必要である10。これに時刻を足して4つの数字を指定して始めて待ち合わせが成立する。つま
りこの場合必要な数字は4つ。これを「4次元」と言う11。
物体の位置だけを問うのなら、3次元でいい。ニュートン力学の世界では、3次元空間と1次元の時間は完全に切り放されて、別個に存在している。相対論的
世界では、空間と時間の間に少し関係が生じてくる。そのため、相対論の話をする時には4次元的記述が好まれる(と、今言ってもわからないだろうけどれど、
授業が進むにつれてわかってくるはずである)。

|
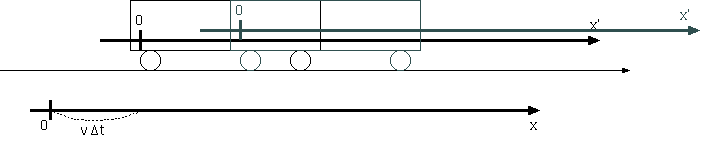
(2.1) |
|
(2.2) |
|
|
(2.4) |
|
(2.5) |
|
(2.6) |
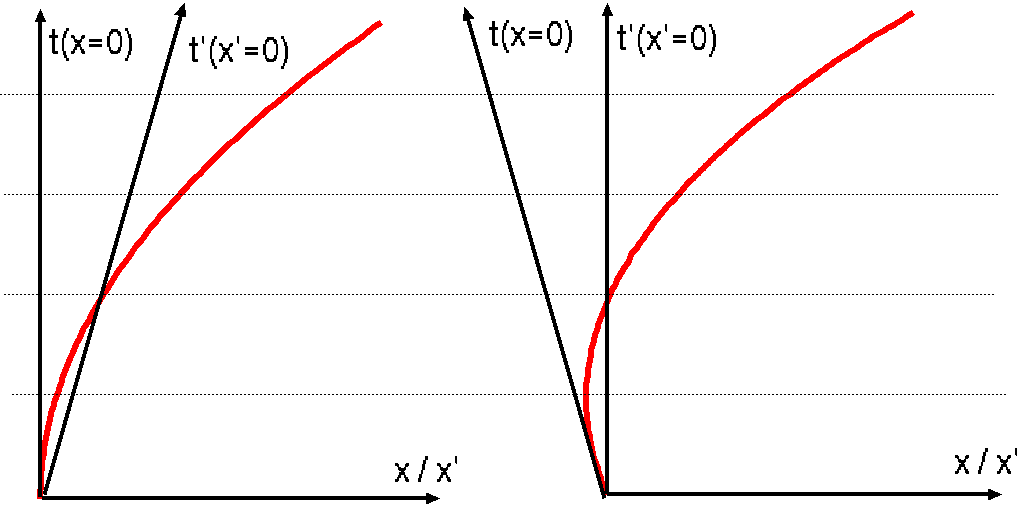 二つの結果を、x系とx′系でグラフにしてみたものが上の二つの図である。x系で見ると「静止した状態の物体が速度を少しずつ増しながら離れていった」
と見える運動であるが、x′系でみると、「最初左へ走っていた物体がだんだん遅くなり、やがて止まって今度は右向きに走りだし、自分の前を通りすぎてどん
どん右へと速度を増しながら離れていった」ということになる。等速運動している自転車を、後から発車した自動車があっという間に追い抜いていった、という
状況である。
上のグラフで、t=t′なのにt軸とt′軸が同じ軸でないことをおかしく思う人もいるかもしれないが、t軸というのはx=0で表される線であり、t′軸
というのはx′=0
で表される線であることに注意せよ。つまりt軸とt′軸が同じ方向を向かないのはxとx′にずれがあるからなのである。この二つのグラフは、グラフを水平
方向(x方向)に、高さ(t座標)に比例した距離だけ横にずらしていくことによって互いに移り変わる。つまり、3+1次元空間のうち、3の部分(空間ある
いは超平面)を時間に応じて動かしていくという変換を行っていることになる。
二つの結果を、x系とx′系でグラフにしてみたものが上の二つの図である。x系で見ると「静止した状態の物体が速度を少しずつ増しながら離れていった」
と見える運動であるが、x′系でみると、「最初左へ走っていた物体がだんだん遅くなり、やがて止まって今度は右向きに走りだし、自分の前を通りすぎてどん
どん右へと速度を増しながら離れていった」ということになる。等速運動している自転車を、後から発車した自動車があっという間に追い抜いていった、という
状況である。
上のグラフで、t=t′なのにt軸とt′軸が同じ軸でないことをおかしく思う人もいるかもしれないが、t軸というのはx=0で表される線であり、t′軸
というのはx′=0
で表される線であることに注意せよ。つまりt軸とt′軸が同じ方向を向かないのはxとx′にずれがあるからなのである。この二つのグラフは、グラフを水平
方向(x方向)に、高さ(t座標)に比例した距離だけ横にずらしていくことによって互いに移り変わる。つまり、3+1次元空間のうち、3の部分(空間ある
いは超平面)を時間に応じて動かしていくという変換を行っていることになる。
|
|
(2.7) |
|
(2.8) |
|
(2.9) |
|
ガリレイ変換によって移り変わるどの慣性系においても、同じ運動の法則が成立する。という原理を「ガリレイの相対性原理」と呼ぶ。この法則の「運動の法則」の部分を電磁気学を含めた「物理法則」に書き換えたいというのが相 対論の目標である。後で詳しく述べるが、その目標達成のために「ガリレイ変換」の部分も「ローレンツ変換」に書き換えられることになる。
ローレンツ変換によって移り変わるどの慣性系においても、同じ物理法則が成立する。というのが「特殊相対性原理」である14。