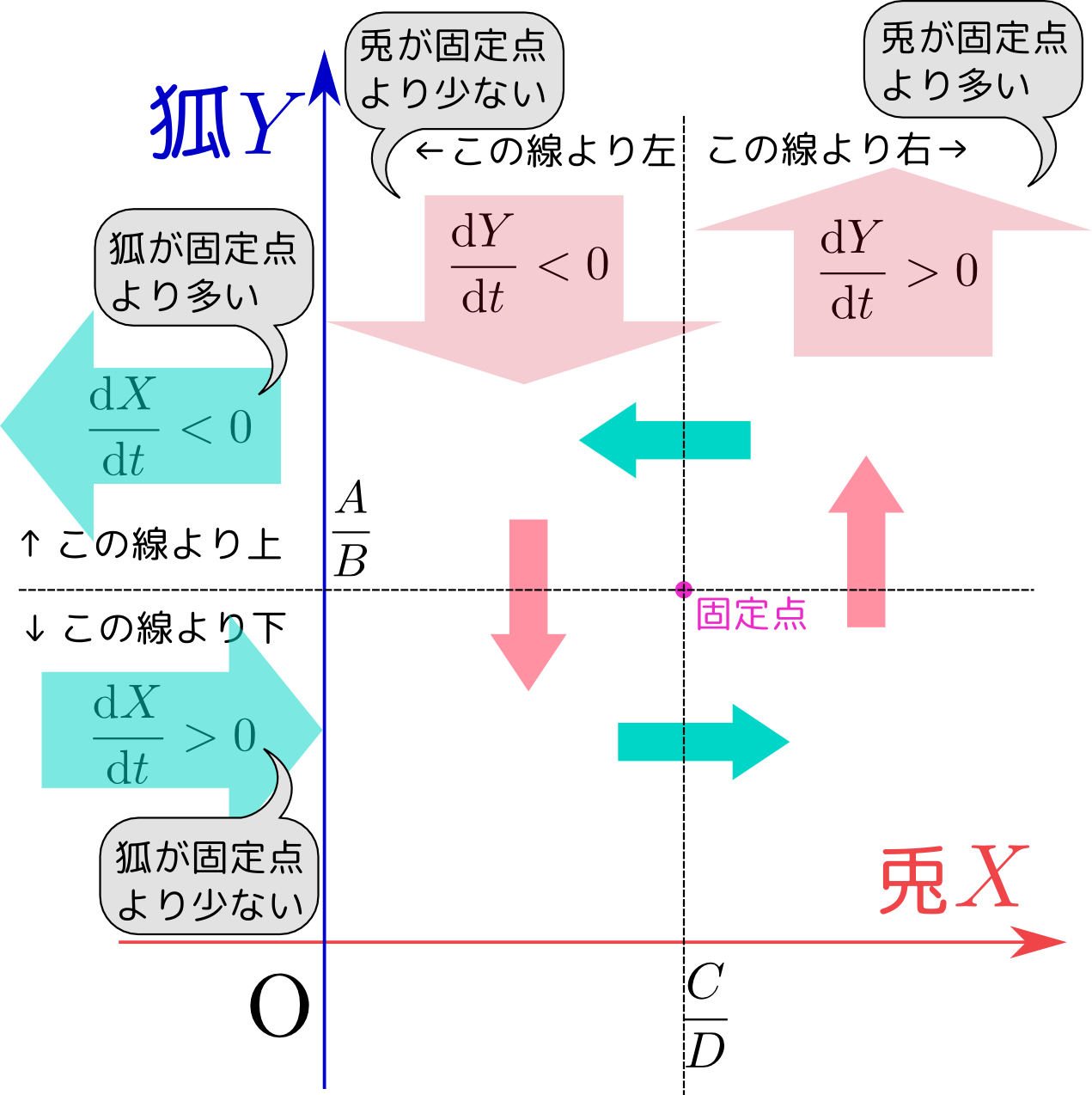
懸垂線

紐を２点を固定してつりさげた時の形を考えてみる。

一番下の部分を原点として、下の図のように座標系を張る。

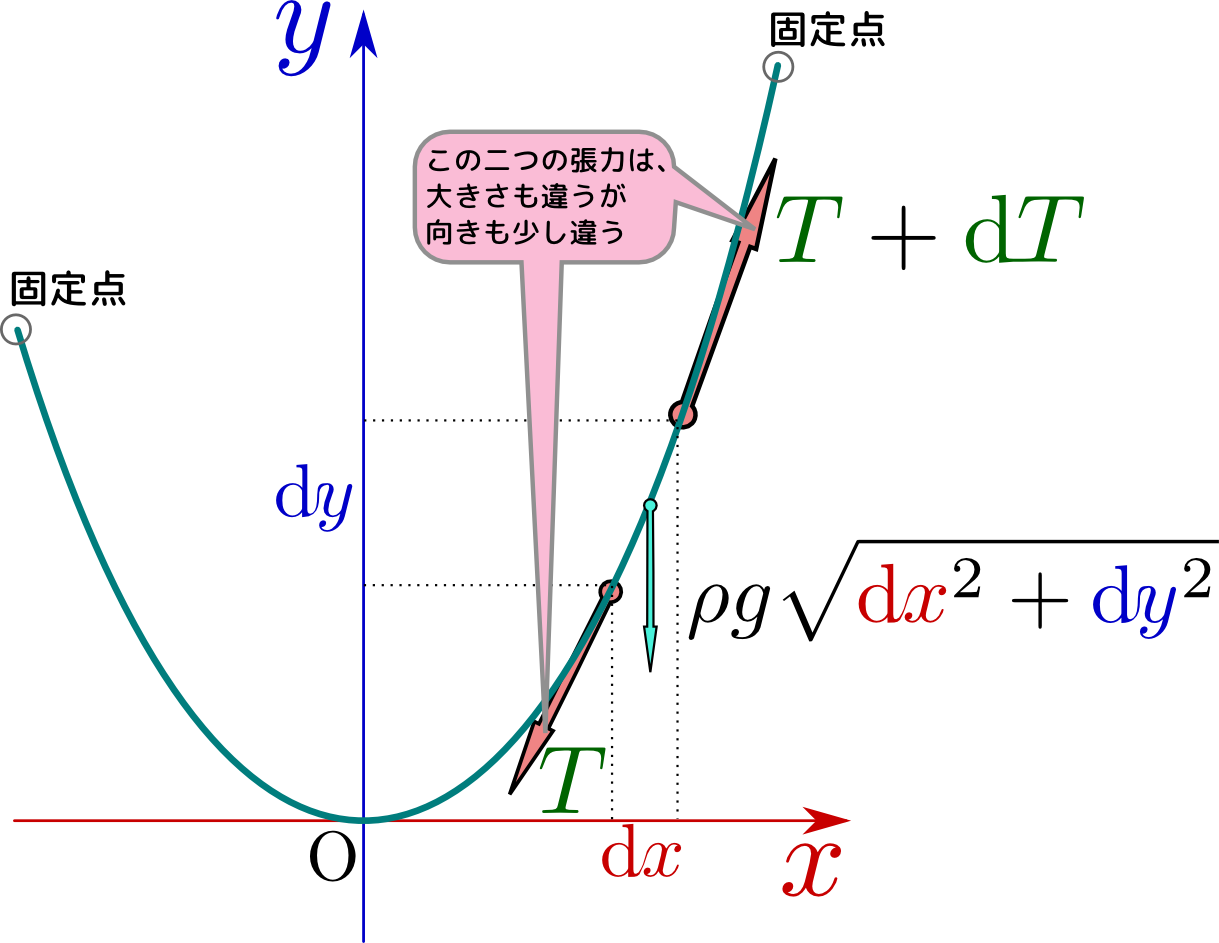
紐にか\かる張力は（垂直に垂らした時と同様に、上の方ほど大きくなるはずだから、図のように微小部分を考えた時、下端には${T}$、上端には${T}+\mathrm dt$の力が働く。紐は直線状ではないからこの張力の向きも（微小に）違う。働く力はこの他に重力がある。微小部分の紐の長さは$\sqrt{\mathrm dx^2+\mathrm dy^2}$だから、これに単位長さあたりの質量$\rho$と重力加速度$g$を掛けた分の重力が下向きに働く。

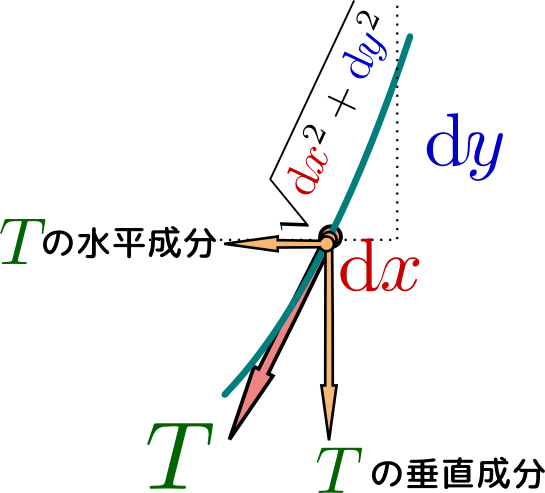
この微小部分に働く張力の水平成分は等しいはずである。よって、

\begin{equation} {T}{\mathrm dx\over \sqrt{\mathrm dx^2+\mathrm dy^2}}=T_0~~~(T_0は定数)\label{suiheiteisuu} \end{equation}

が成り立つ。ここで$T_0$は、$\mathrm dy=0$の時の張力だと思えばよい（図を見ると、それは最下点すなわち原点である）。

次に垂直成分を考えると、${T}$の垂直成分の増加がちょうど重力によって打ち消されればつりあいが保たれるから、「${T}$の垂直成分の微分」が、その微小部分にかかる重力に等しくなる。式で表現すれば、

\begin{equation} \mathrm d \left( {T}{\mathrm dy\over \sqrt{\mathrm dx^2+\mathrm dy^2}} \right)=\rho g \sqrt{\mathrm dx^2+\mathrm dy^2} \end{equation}

が成り立つということである。

上の式から、${T}=T_0{\sqrt{\mathrm dx^2+\mathrm dy^2}\over \mathrm dx}$として代入して、

\begin{equation} \mathrm d \left( T_0{\mathrm dy\over \mathrm dx} \right)=\rho g \sqrt{\mathrm dx^2+\mathrm dy^2} \end{equation}

となる。$T_0$は定数だから微分の外に出して、右辺は$\mathrm dx$をルートの外に出し、

\begin{equation} T_0\mathrm d \left({\mathrm dy\over \mathrm dx}\right)=\rho g\sqrt{1+\left({\mathrm dy\over \mathrm dx}\right)^2}\mathrm dx \end{equation}

とした上で、${\mathrm dy\over \mathrm dx}=V$と考えれば

\begin{equation} \mathrm dV= {\rho g\over T_0}\sqrt{1+V^2}\mathrm dx \end{equation}

という変数分離可能な微分方程式になる。$\sqrt{1+V^2}$という形が出てきたので、$V=\sinh {t}$という置換積分（$\mathrm dV=\cosh {t} \mathrm dt$となる）を使って計算して、

\begin{equation} \begin{array}{rll} {\mathrm dV\over \sqrt{1+V^2}}=&{\rho g\over T_0}\mathrm dx &{V=\sinh {t}として} \\ {\cosh {t} \mathrm dt\over \cosh {t}}=&{\rho g\over T_0}\mathrm dx &{積分して} \\ {t}=&{\rho g\over T_0}x+C~~~&(Cは積分定数) \end{array} \end{equation}

であるから、

\begin{equation} V={\mathrm dy\over \mathrm dx}= \sinh \left({\rho g\over T_0}x+C\right) \end{equation}

となる。これをさらに積分して、

\begin{equation} y= {T_0\over \rho g}\cosh \left({\rho g\over T_0}x+C\right)+D~~~(Dは積分定数) \end{equation}

が解となる。最初に図で設定したように$x=0$で$y=0,{\mathrm dy\over \mathrm dx}=0$とすれば、$C=0,D={-{T_0\over \rho g}}$となり、最終的な答えは

\begin{equation} y= {T_0\over \rho g}\left( \cosh \left({\rho g\over T_0}x\right)-1\right)\label{kensui} \end{equation}

となる。このような曲線（$\cosh$で表される）を「懸垂線」と呼ぶ。最初「放物線？」と思った人がいたが、計算結果は$\cosh$である。しかし

\begin{equation} \cosh x =1+{1\over 2}x^2 + {1\over 24}x^4+\cdots \end{equation}

という展開であることを考えると、$x$が小さい範囲ではこの式は$y=ax^2$とほぼ同じである。

肉食動物と草食動物の連立微分方程式

←第23講へ　講義録目次ページに戻る

肉食動物と草食動物の連立微分方程式

草食動物（兎）と肉食動物（狐）の数（それぞれ$X$と$Y$とする）がどう増減するかを考える。狐は兎を食べるので、兎は狐と出会うと死ぬと考えよう。出会う確率は$X$と$Y$の積に比例すると考えると、兎の減少量も積$XY$に比例するだろう。

兎は草食で、草はなくならないとすれば、狐に出会わなければ今いる量$X$に比例して増える。よって、

\begin{equation} {\mathrm dX\over \mathrm dt}= AX -BXY\label{lwone} \end{equation}

という式で増減するとする（$A,B$は比例定数）。

一方狐は、兎を食べないと生きていけないのだから、その増加はどれだけ兎を食べられるかによって決まり、それは$XY$に比例するのだったから、狐は$XY$に比例して増える。兎がいなかったら寿命が来て死ぬだけなので、それを$-CY$という形で式に入れて

\begin{equation} {\mathrm dY\over \mathrm dt}= -C Y + D XY\label{lwtwo} \end{equation}

という微分方程式に従うことになる（$C,D$は$A,B$とは別の比例定数である）。この方程式はこの式を出した二人の数学者の名前を取って「ロトカ・ヴォルテラの方程式」と呼ばれる。

時間変化を考えるには、${\mathrm dX\over \mathrm dt},{\mathrm dY\over \mathrm dt}$に関する二つの微分方程式を連立させて解けばよいわけである。いきなり解けと言われるとどうしていいのか悩んでしまうところだが、ここでまず、「${\mathrm dX\over \mathrm dt}={\mathrm dY\over \mathrm dt}=0$となるのはどんなときか？」から考えるのがよい。これはつまり$X,Y$が時間変化しなくなる状況なので「固定点」と呼ぶ。固定点を求める方程式は

\begin{equation} AX-BXY = X(A-BY)=0,~~~~-CY + DXY=Y(-C+DX)=0 \end{equation}

である。

この方程式は$X=Y=0$という解を持つが、これは「兎も狐もいない」という「つまらない解」なので考えないことにする。つまり、$X={C\over D},Y={A\over B}$が意味のある固定点である。

固定点からずれた時の${\mathrm dX\over \mathrm dt},{\mathrm dY\over\mathrm dt}$の様子をグラフに表示すると下のグラフのようになる。これから$X$-$Y$平面内で反時計周りにぐるぐる回るような時間発展を行うということが予想される。

固定点からのずれを$x,y$とする。つまり、

\begin{equation} X= {C\over D}+x,~~Y={A\over B}+y \end{equation}

とする。こうして$x,y$の微分方程式を作ると、

\begin{equation} {\mathrm dx\over \mathrm dt}= -B \left({C\over D}+x\right) y,~~~ {\mathrm dy \over \mathrm dt}= D\left({A\over B}+y\right)x \end{equation}

となる。ここで$x,y$は${C\over D},{A\over B}$に比べて小さいと考えて、括弧内の$x,y$は無視して、

\begin{equation} {\mathrm dx\over \mathrm dt}= -{BC\over D} y,~~~ {\mathrm dy \over \mathrm dt}= {AD\over B} x \end{equation}

と近似する。第一式を微分して

\begin{equation} {\mathrm d^2 x\over \mathrm dt^2}= -{BC\over D} {\mathrm dy\over \mathrm dt} \end{equation}

にしてから第二式を代入すると

\begin{equation} {\mathrm d^2 x\over \mathrm dt^2}= -{BC\over D}\times{AD\over B}x=-{AC}x \end{equation}

という、単振動と同じ式が出てくる。解はすでに知っていて、

\begin{equation} x(t)=x_0 \cos \left(\sqrt{AC}t+\alpha\right) \end{equation}

と書ける（$x_0,\alpha$は微分方程式からは決まらない）。${\mathrm dx\over \mathrm dt}=-{BC\over D} y$なので、

\begin{equation} \begin{array}{rl} -\sqrt{AC}x_0 \sin \left(\sqrt{AC}t+\alpha\right)= &-{BC\over D} y(t) \\ {D\over BC}\times\sqrt{AC}x_0 \sin \left(\sqrt{AC}t+\alpha\right)= &y(t) \end{array} \end{equation}

で$y$も求まる。

$X,Y$の時間変化を表すのが次のグラフである。

$x,y$と$X,Y$は定数を足しただけの違いなので、$X$（兎）の変化は$\cos$で、$Y$（狐）の変化は$\sin$で表されていると思えばよい。

グラフに示したように、狐のグラフが「山」である間は兎のグラフは右下がり、狐のグラフが「谷」である間は兎のグラフが右上がりとなる。もちろんこれは「狐が多くて兎が食われる時期は兎が減り、狐が少なくなると兎が増える」ということを示している。逆に「兎が多いと狐が増える（およびこの逆）」もわかる。グラフを見ながらそれを確認してみよう。

ここで求めたのは近似解なので、$X$-$Y$平面に描かれる図形は単純な楕円であるが、実際に微分方程式をちゃんと解いてみると少々複雑な図形を描く。

X=

Y=

初期値変更 グラフ消去

この場合は$(X,Y)=(1,1)$が固定点であり、その周りをめぐる軌跡を描く。固定点からの外れが小さい領域では軌跡は円に近い（楕円でなく円なのは今の場合は${D\over BC}=1$だから）。

「狐が少ないと兎は急激に増える」「増えた兎は狐が食うことによって減る（この時同時に狐が増える）」「兎を食いつくすと狐も減る」という現象が起きていることが、グラフからも感じられる。

懸垂線 受講者の感想・コメント

←第23講へ　講義録目次ページに戻る

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

肉食動物と草食動物の連立微分方程式

第23講へ　講義録目次ページに戻る