まず、よく使う式をまとめておこう。ここまでで「微分」という演算の意味がわかっていれば、どの性質も少し考えれば納得できるはずである。
微分の性質
という言葉はこの後もよく出てくる。これは
の二つの性質を合わせ持っているということである。
確認するには、$\alpha f({x})+\beta g({x})$を微小変化させてみればよい。
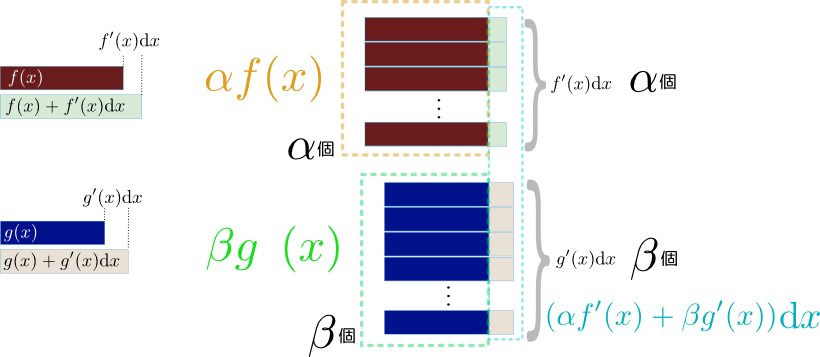
\begin{equation} \begin{array}{rl} \alpha f({x}+\mathrm dx)+\beta g({x}+\mathrm dx) =& \alpha \underbrace{(f({x})+f'({x})\mathrm dx)}_{\small f({x}+\mathrm dx)}+\beta \underbrace{(g({x})+g'({x})\mathrm dx)}_{\small g({x}+\mathrm dx)} \\ =&\alpha f({x})+\beta g({x}) +\underbrace{(\alpha f'({x})+\beta g'({x}))}_{\left(\alpha f({x})+\beta g({x})\right)'}\mathrm dx \\ \end{array} \end{equation}となって線型性が確認できる(ここ以後しばらくの計算では${\cal O}((\mathrm dx)^2)$には興味がないので、常に省略する)。この式をあえて図で表現しておくと以下のようになる。

次のライプニッツ則は具体的には、
\begin{equation} \begin{array}{rl} f({x}+\mathrm dx)g({x}+\mathrm dx) =&\underbrace{(f({x})+f'({x})\mathrm dx)}_{\small f({x}+\mathrm dx)}\underbrace{(g({x})+g'({x})\mathrm dx)}_{\small g({x}+\mathrm dx)}\\ =&f({x})g({x})+f'({x})g({x})\mathrm dx+f({x})g'({x})\mathrm dx\\[3mm] =&f({x})g({x})+\underbrace{(f'({x})g({x})+f({x})g'({x}))}_{(f({x})g({x}))'}\mathrm dx\\ \end{array} \end{equation}という計算をやると、右辺の$\mathrm dx$の1次のオーダーの係数(つまり、微係数)が$f'({x})g({x})+f({x})g'({x})$であることがわかる。下の図はこの微分演算の時に行われている微小変化のイメージである。
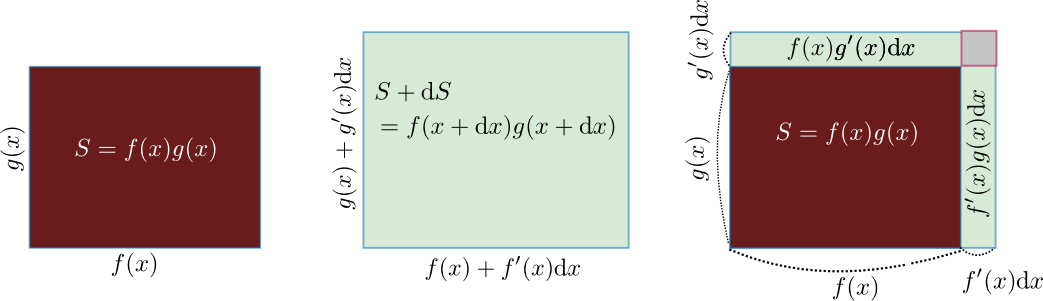
最後に{\bf 合成関数の微分}(このルールは「連鎖律(chain rule)」とも呼ばれる)を数式で表現しておこう。$g(f({x}))$という合成関数を考えて、その独立変数${x}$を${x}+\mathrm dx$と微小変化させる。
結果、$f({x})$は
\begin{equation} f({x}+\mathrm dx)= f({x})+ \underbrace{f'({x})\mathrm dx}_{\mathrm{d} (f({x}))} \end{equation}へと変化する。ここで$\mathrm{d} (f({x}))=f'({x})\mathrm dx$という記号を使った。$\mathrm{d}(なんとか)$のように$\mathrm{d} $をつけることで「(なんとか)の微小変化」という意味を持たせるこれをさらに省略して$\mathrm df({x})$、さらに$({x})$も省略して$\mathrm df$とだけ書いたりもする。。ライプニッツの記号の方を使うと、$\mathrm{d} (f({x}))={\mathrm df\over \mathrm dx}({x})\mathrm dx$と書けて、この式を「$\mathrm dx$を約分している」というイメージで捉えることができる。
$f({x})$の${x}$が微小変化すると、$g(f({x}))$は
\begin{equation} g(f({x}+\mathrm dx))= g(f({x})+\underbrace{f'({x})\mathrm dx}_{\mathrm{d}(f({x}))}) \end{equation}と微小変化する。上にも書いたように、$f'({x})\mathrm dx$の部分を$\mathrm{d} (f({x}))$と考えれば、
\begin{equation} g(f+\mathrm{d} (f({x})))= g(f)+g'(f)\mathrm{d} (f({x})) \end{equation}という展開をもう一度考えて、
\begin{equation} g(f({x}+\mathrm dx))= g(f({x}))+ g'(f({x}))\underbrace{f'({x})\mathrm dx }_{\mathrm{d} (f({x}))} \end{equation}とすることで、$g(f({x}))$の導関数が$g'(f({x}))f'({x})$だとわかる。
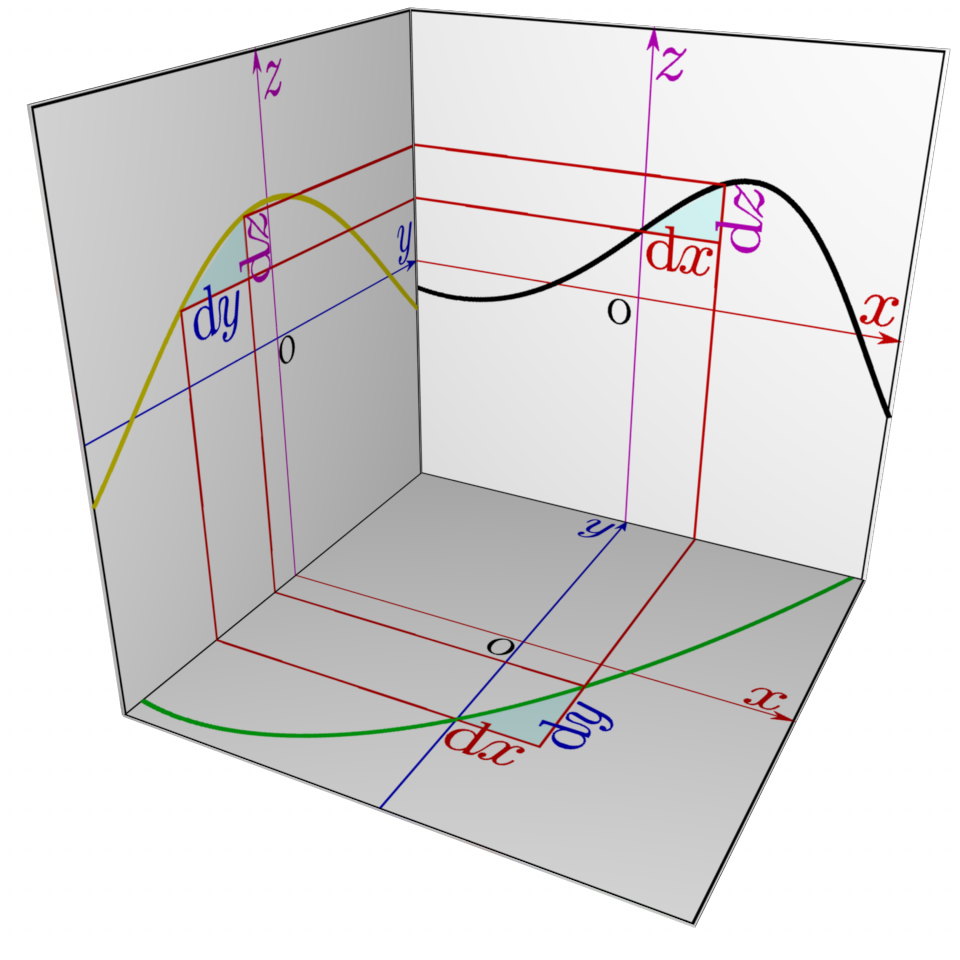
これを図で表現したのが右の図である。合成関数のときのように、${x}\to{y}\to{z}$(${y}=f({x}),{z}=g({y})$)という関係がある時、${x}$を微小変化させた時にそれに応じて${y}$が、そして連鎖して${z}$が変化する。
図には三つの導関数
$${\mathrm dy\over \mathrm dx}({x}),{\mathrm dz\over \mathrm dy}({y}),{\mathrm dz\over \mathrm dx}({x})$$を表す三角形(この三角形の傾きが導関数の値)が描かれている。導関数は$\mathrm dx,\mathrm dy,\mathrm dz$という三つの微小量の比でここでも計算しているのは微小変化の「比」だけであって、微小変化そのものではない。計算されるものだから、
\begin{equation} {\mathrm dz\over \mathrm dy}({y}) {\mathrm dy\over \mathrm dx}({x})={\mathrm dz\over \mathrm dx}({x})~~~~ただし、{y}=f({x}) \end{equation}が成立する。
\begin{equation} {\mathrm dz\over {\mathrm dy}}{{\mathrm dy}\over \mathrm dx}={\mathrm dz\over \mathrm dx} \end{equation}という「約分」を行った、と考えてもよい。
例として$F({x})=({x}^2+{x})^3$の微分をしてみよう。これを$f({y})={y}^3,{y}=g({x})={x}^2+{x}$として、$F({x})=f(g({x}))$と考えてから微分すると、
\begin{equation} {\mathrm{d} \over \mathrm dx}F({x})=\underbrace{ {\mathrm{d} \over \mathrm dx}g({x})}_{(2{x}+1)} \underbrace{ {\mathrm{d} \over \mathrm dy}f({y})}_{3{y}^2} = 3(2{x}+1)({x}^2+{x})^2 \end{equation}となる。慣れてきたら${y}$を導入するのも省略して、
\begin{equation} \begin{array}{rrl} & ({x}^2+{x})^3+ \mathrm{d} \left(({x}^2+{x})^3\right)=& \left( {x}^2 + {x} + \mathrm{d} ({x}^2+{x}) \right)^3 \\ &\mathrm{d} \left(({x}^2+{x})^3\right)=& \left( {x}^2 + {x} + \mathrm{d} ({x}^2+{x}) \right)^3- ({x}^2+{x})^3\\ &\mathrm{d} \left(({x}^2+{x})^3\right)=&3\left( \mathrm{d} ({x}^2+{x})\right) ({x}^2+{x})^2\\ &=&3(2{x}+1)({x}^2+{x})^2\mathrm dx \end{array} \end{equation}のように計算したってよい。
$x^2,x^3$の場合をここまで考えたが、$x^n$の微分も同様に
\begin{equation} {y}+\mathrm dy=\underbrace{({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)\cdots }_{n個} \end{equation}の中にある$\mathrm dx$の1次は$n$個の${x}^{n-1}\mathrm dx$であろうと考えるか、もしくは
\begin{equation} \underbrace{{y}}_{これが変化すると}=\underbrace{\overbrace{ {x}\times{x}\times{x}\times{x}\times{x}\times{x}\times{x}\times\cdots }^{n個}}_{\tiny このうち一つが\mathrm dx 変化したもの\atop が全部でn種類出てくる} \end{equation}と考える(二つ以上の${x}$が変化して$\mathrm dx$になったものは、${\cal O}(\mathrm dx^2)$となって出てこない)と、
\begin{equation} \mathrm dy = n{x}^{n-1}\mathrm dx~~~すなわち、{\mathrm dy\over \mathrm dx}= n{x}^{n-1} \end{equation}と分かる。
上の式は$n$が自然数なら正しい。では、指数が負の整数ならどうなるだろうか。その場合は、${y}={x}^{-n}$をまず、${x}^n {y}=1$に直してから、その微小変化を考えると、
\begin{equation} \begin{array}{rll} \underbrace{({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)\cdots }_{n個}\times({y}+\mathrm dy)=&1\\ \underbrace{{x}^n {y}}_1 + n{x}^{n-1}\mathrm dx{y} + {x}^n \mathrm dy =&1\\ {x}^n \mathrm dy =&-n{x}^{n-1}\mathrm dx \underbrace{{x}^{-n}}_{{y}} \\ \mathrm dy =& -n {x}^{-n-1}\mathrm dx\\ \end{array}\label{fubekibibun} \end{equation}となる慣れてきたら、「${x}^n {y}=1$の両辺を微分する」の一言で$n{x}^{n-1}\mathrm dx {y}+ {x}^n \mathrm dy =0$を出してよい。(結果${\mathrm dy\over \mathrm dx}= -n x^{-n-1}$を上の${\mathrm dy\over \mathrm dx}=nx^{n-1}$と見比べると、単に$n\to -n$と置き換えただけの式になっている)。
指数が整数でない場合についても考えよう。たとえば${y}={x}^{1\over n}$については、これをまず${y}^n = {x}$になおしてから、
\begin{equation} \underbrace{({y}+\mathrm dy)({y}+\mathrm dy)({y}+\mathrm dy)({y}+\mathrm dy)\cdots }_{n個}= {x}+\mathrm dx \end{equation}とすれば(これまで同様、1次のオーダーを取り出すことで)こちらも慣れてくれば、${y}^n = {x}$からすぐに$n {y}^{n-1}\mathrm dy = \mathrm dx$が出せるだろう。、
\begin{equation} \begin{array}{rl} n {y}^{n-1}\mathrm dy =& \mathrm dx\\ {\mathrm dy\over \mathrm dx} =& {1\over n {y}^{n-1}}={1\over n}{x}^{{1\over n}-1}\\ \end{array} \end{equation}がわかる。同様に、${y}={x}^{m\over n}$に関しても${y}^n={x}^m$としてから
\begin{equation} \begin{array}{rl} \underbrace{({y}+\mathrm dy)({y}+\mathrm dy)({y}+\mathrm dy)({y}+\mathrm dy)\cdots }_{n個}=& \underbrace{({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)\cdots }_{m個}\\ n{y}^{n-1}\mathrm dy =& m {x}^{m-1}\mathrm dx \end{array} \end{equation}のように考えれば、
\begin{equation} {\mathrm dy \over \mathrm dx}= {m\over n} {x}^{{m\over n}-1} \end{equation}が示せるから、一般の有理数$\alpha={m\over n}$に対して${y}={x}^\alpha$の微分は
\begin{equation} {\mathrm dy\over \mathrm dx}= \alpha {x}^{\alpha-1} \end{equation}としてよい。ここまでくれば、「無理数に対しても極限操作で定義すればよさそうだ」とわかるので、$\alpha$は任意の実数でよい。この式を見ると微分により${x}$の冪を1ずつ下がることが言える。例外は定数(すなわち$x^0$の時)で、この時だけは$(定数)\times x^{-1}$とはならず、0となるでは微分すると$x^{-1}={1\over x}$になる関数はないのかというと、ちゃんとある。。
ここでは$x^\alpha$だけを考えたが、すでに微分が線型性を持つことは知っているので、
\begin{equation} {\mathrm{d} \over \mathrm dx}\left( a {x}^\alpha + b {x}^\beta + c{x}^\gamma+\cdots\right) = a\alpha {x}^{\alpha-1}+ b\beta {x}^{\beta-1}+ c\gamma {x}^{\gamma-1}+\cdots \end{equation}のように冪の和の微分も簡単にできる。