三角関数の微分（sin）

sinの微分

まず数式で考えていく。

三角関数の加法定理

\begin{equation} \sin (A+B)=\cos A\sin B+\sin A\cos B,~~ \cos (A+B)=\cos A\cos B-\sin A\sin B \end{equation}

を使って

\begin{equation} \sin ({\theta}+\mathrm d\theta)=\cos {\theta} \sin \mathrm d\theta + \sin {\theta} \cos \mathrm d\theta \end{equation}

という式を出す。ここで$\mathrm d\theta$は0に近づけるのだから${\cal O}(\mathrm d\theta^2)$は書かないことにすると、$\sin \mathrm d\theta =\mathrm d\theta$であり、$\cos\mathrm d\theta=1$であるから、

\begin{equation} \sin ({\theta}+\mathrm d\theta)= \sin {\theta}+\underbrace{\cos {\theta}}_{微係数}\mathrm d\theta \end{equation}

となる（$f({x}+\mathrm dx)=f({x})+f'({x})\mathrm dx$と比較せよ）。これから、

sinの微分

\begin{equation} \begin{array}{rl} {\mathrm d }(\sin {\theta})=&\cos{\theta} \mathrm d\theta,~~~~ {\mathrm d \over \mathrm d\theta}(\sin {\theta})=\cos{\theta} \end{array} \end{equation}

である。

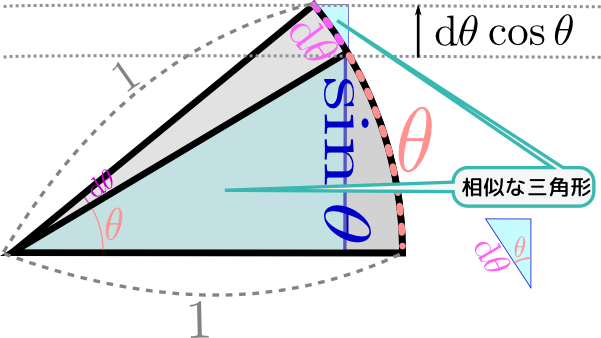
次に、同じことを図で考えよう。

上のように、角度${\theta}$を$\mathrm d\theta$だけ変化させた時の、（三角形の高さ）である$\sin\theta$の変化を考える。図に「相似な三角形」として示している「小さい方の三角形の斜辺は曲線だから相似な三角形とは言えないぞ！」と思う人もいるかもしれないが、今$\mathrm d\theta$をどんどん小さくしているので、この曲線は限りなく直線に近いのである。ように、$\mathrm d\theta$という長さの弧を斜辺として微小な直角三角形ができていて、この直角三角形の高さにあたる部分が$\mathrm d\theta \cos{\theta}$である。つまり$\sin {\theta}$の微小変化が$\cos {\theta} \mathrm d\theta$と書けるのだから、微係数は$\cos \theta$である。

では、これを動画で実感しよう。

　下左の図は半径１の円（単位円）を描いたもので、中心から円周の一点に向かっている棒の角度に応じて、sinθ,cosθの値が決まる。

↑の棒の角度はドラッグによって変えることができる。

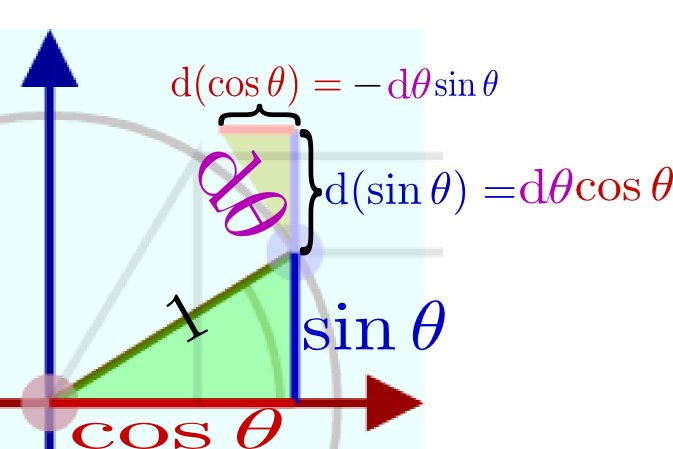
　アニメーションのように、θが変化していったときに縦軸の座標sinθと横軸の座標cosθがどのように変化していくかを考えると、それぞれの微分がどうなるかがわかる（はずである）。

　左の図は上のグラフに長さを描き込んだものである。θが変化したことによる「高さ」sinθの変化量であるd(sinθ)がdθ×cosθに等しいことが読み取れる。

　右側のグラフはsinθ,cosθのグラフであるが、そちらにも、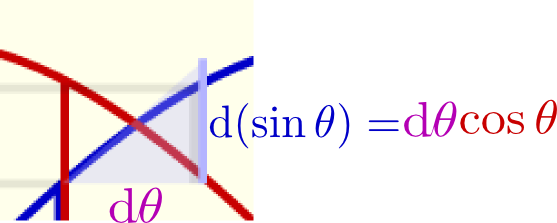のように傾きが表示してある。この「傾き」が確かにcosθに比例していることを確認しよう。

　動径の棒をドラッグして動かすことができるので、いろんな場合について確かにsinθの変化（増減）がcosθに比例していることを動かしながら実感して欲しい。

←最初のページへ　cosの微分のページへ→