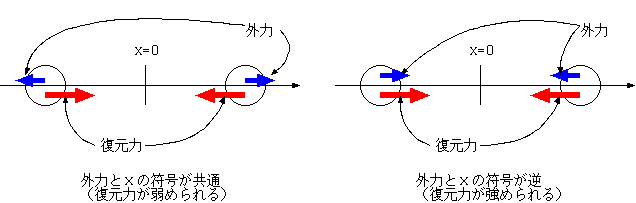
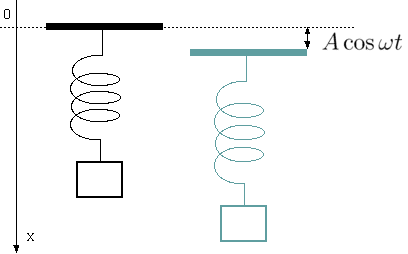
ω0 > ωでは、物体の位置xと外力が同符号になっている。それが左の図で、この時、復元力(xと逆じ振動)と外力は逆を向く。
結果として「復元力を弱くした」のと同じことである。すると当然、実際に起こる振動の周期は外力がない時より長くなる。ω0 < ωの時はこの逆で、外力は復元力を強めるので、周期は短くなる。
 ここで、C′=0の場合を考察しておこう。その
場
合、
ここで、C′=0の場合を考察しておこう。その
場
合、
|
(2.24) |

|
(2.25) |
|
(2.26) |
|
(2.27) |
|
(2.28) |
|
(2.29) |
|
(2.30) |
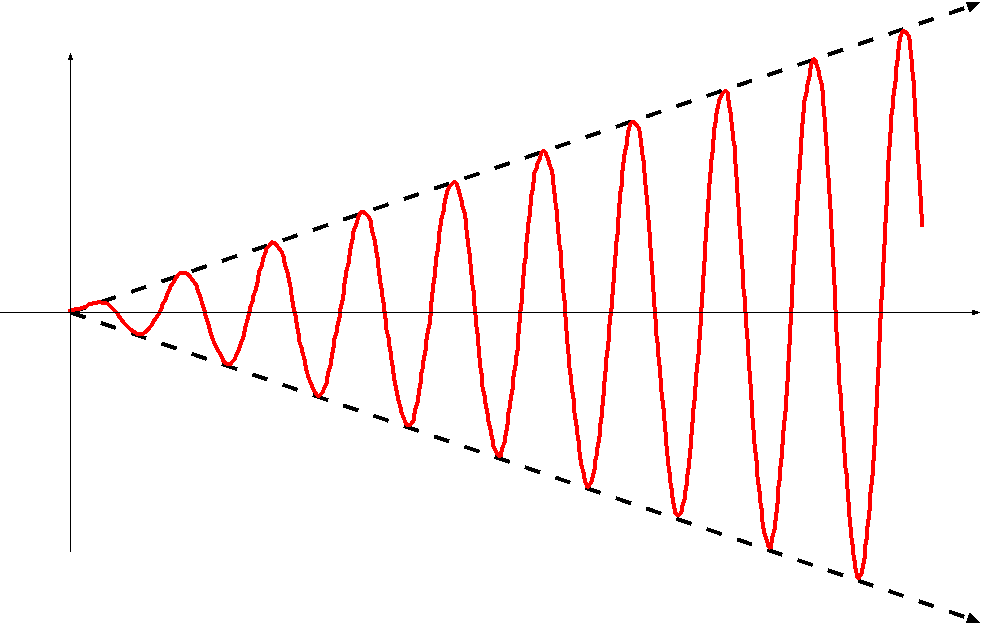 共振・共鳴は、いろんなスケールの物理現象において見られる。子供がブランコをこぐことによって振れ幅を大きくしていくのも共振の一種であるし、原子レベ
ルでも共振現象は現れる。たとえば物質に電磁波をあてると、特定の振動数をあてた時に限ってその電磁波のエネルギーが大きく吸収される、というようなこと
が起こる。これはその物質の固有振動数と電磁波の振動数が近いために共振が起こり、結果として電磁波のエネルギーが原子の振動に効率よく変化するからであ
る。
共振・共鳴は、いろんなスケールの物理現象において見られる。子供がブランコをこぐことによって振れ幅を大きくしていくのも共振の一種であるし、原子レベ
ルでも共振現象は現れる。たとえば物質に電磁波をあてると、特定の振動数をあてた時に限ってその電磁波のエネルギーが大きく吸収される、というようなこと
が起こる。これはその物質の固有振動数と電磁波の振動数が近いために共振が起こり、結果として電磁波のエネルギーが原子の振動に効率よく変化するからであ
る。
|
(2.31) |
|
(2.32) |
| 単振動の場合 | LC回路の場合 | |
| 変位 | x | Q |
| 変位の変化率 | [dx/dt] | I=[dQ/dt] |
| その変化率 | [(d2 x)/(dt2)] | [dI/dt]=[(d2 Q)/(dt2)] |
| 慣性を司るパラメータ | m | L |
| 復元力を司るパラメータ | k | 1/C |
方程式 |
m[(d2 x)/dt2]=−kx |
L[(d2Q)/(dt2)] = −Q/C |
| 角振動数 | √{[k/m]} | [1/√[LC]] |
|
共振によって起こった事故
1850年、フランスで吊り橋の上を兵隊500人が行進した時、吊り橋の振動の固有振動と兵隊の行進の歩調がそろってしまったために吊り橋が大きく振動 して橋が落ちた、という事故があった。以来、「吊り橋の上で足並みを揃えるな」という立て札が立てられたと言う。 建築においては共振現象は問題とされており、たとえば地震に強い建物を造るために、建物の固有振動数が地震の振動数と一致しないように工夫したりする。 |
|
(2.33) |
|
(2.34) |
|
(2.35) |
|
(2.36) |
|
(2.37) |
|
(2.38) |
|
(2.39) |
|
(2.40) |
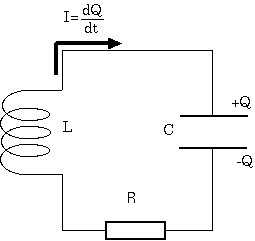 |
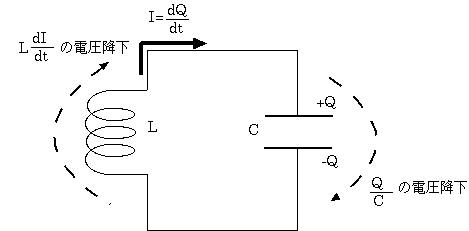
左の図で示される電気回路について、
|
 |
|
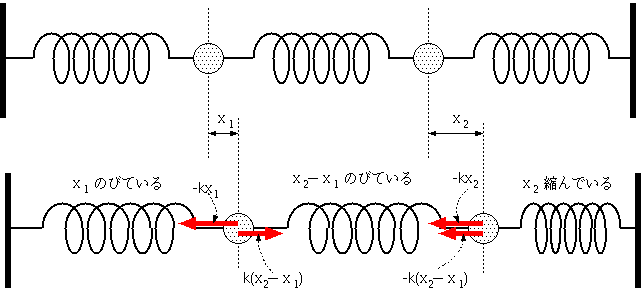
この章で学ぶ大事なこと
- 連成振動の運動方程式の解き方
- 「モード」の概念と、その使い方
|
|
|
|
(3.7) |
|
(3.8) |
|
(3.9) |
|
(3.10) |
|
(3.11) |