卒研生: 大善 雄, 杉村 美沙
本研究の概要
私達は球対称の中性子星と、高速回転により変形した中性子星の構造の計算を行いました。 また、高速回転のために非軸対称的な変形をした中性子星から放出される重力波の振幅を、四重極公式を用いて計算しました。 そしてこの重力波の計算結果を、レーザー干渉計型重力波検出器のノイズカーブと比較し、観測可能性を議論しました。
このページでは中性子星の構造の計算について説明します。
中性子星とは
中性子星とは、初期の質量9〜25太陽質量程度の恒星が進化して、最終的に鉄のコアが重力崩壊をしてできる星です。 重力崩壊の段階では重力波が放出されます。
また、鉄のコアの角運動量をほぼ保存したまま収縮するので、できたばかりの原始中性子星は非常に高速回転しています。 このような星は非軸対称になっている可能性があり、その場合にも重力波が放出されます。
中性子星vs沖縄
首里城に典型的な中性子星を持ってくると、この程度の大きさになります。 中性子星は、半径10キロメートル、質量1.4太陽質量程度の非常に高密度な天体です。
中性子星の限界質量は1.4〜3太陽質量といわれています。 これより重い場合には重力が中性子の縮退圧に打ち勝って極限まで収縮し、ブラックホールになります。
中性子星の構造
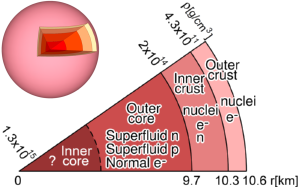
質量1.4太陽質量、半径10.6kmの球対称な中性子星モデルを例にして構造を説明します。 横軸を中心からの距離、斜めの軸を密度にとり、中性子星の一部を切り取った断面図を示しました。
中性子星は中心部が最も密度が高く、外側へ行くにつれて減少していきます。
- Inner core
- 密度は原子核密度の数倍から10倍程度になっています。 この領域の高密度な物質の状態については、様々な説が挙げられており、まだよくわかっていません。
- Outer core
- 超流動している中性子と、数%の陽子や電子が含まれます。
- Inner crust
- 原子核密度2×1014g/cm3より外側の領域をCrustと呼びます。 厚さは約600mで、原子核や電子、自由中性子の流体が存在します。
- Outer crust
- 鉄などの原子核でできた固体で、厚さは300mほどです。
中性子星の理論
中性子星のつりあい
中性子星は、内側へ向かう自己重力と、外側へ向かう圧力で支えあっています。
中性子星は非常に重いため、計算するには一般相対論が必要になるので、 アインシュタイン方程式を使って重力を決めます。 一般のメトリック
に対するアインシュタイン方程式は次のように書けます。
さらに流体の運動方程式、静止質量保存の式も用います。
Gαβはアインシュタインテンソル、Tαβはエネルギー運動量テンソル
で、ρは静止質量密度、uαは流体の四元速度、Pは圧力、εはエネルギー密度です。
なお、ここではG=c=1unit を使用します。
球対称モデルのための定式化
球対称モデルの計算をするにあたって、球対称時空のメトリック
を用いてアインシュタイン方程式を変形すると、 Tolman-Oppenheimer-Volkoff(TOV)方程式が導かれます。
mは質量、rは中心からの距離です。
TOV方程式に対して状態方程式を与えると積分することができて、球対称な中性子星の内部の構造が計算できます。
回転中性子星の計算
回転中性子星の計算には、IWM formulation を使います。メトリック
を使い、IWM formulation によって重力場の方程式を定式化すると、 次のような方程式になります。
また、流体の運動方程式は静水平衡の式に書き直されます。
これらの方程式を解く数値計算コードは、Xing Huang, Charalampos Markakis, Noriyuki Sugiyama, Koji Uryu, PRD 78(2008) で瓜生先生が開発しました。 私はこれに、次で述べる Parametrized Equation of State を組み込みました。
状態方程式
中性子星の構造を計算するにあたって、圧力を決める状態方程式が必要となります。 しかし、高密度物質の理論モデルはまだよくわかっておらず、 様々な状態方程式が提案されています。
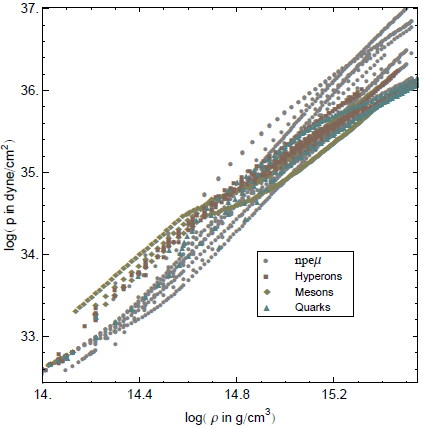
Read et al., arXiv:0812.2163(2008)
この図は、様々な理論のモデルから導かれた高密度物質の状態方程式です。 これはデータテーブルで与えられています。 横軸は密度、縦軸は圧力で、 密度1015g/cm3において圧力がどの程度になっているかを示しています。
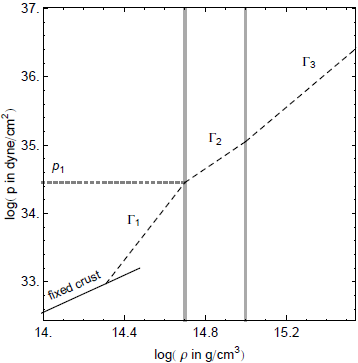
Read et al., arXiv:0812.2163(2008)
私達はこれに対し、最近開発されたParametrized Equation of State (PEOS) を用いて 高密度物質の状態方程式を近似しました。 PEOSとは、図のように密度を区間に分けて、その区間ごとにKとΓを設定して Polytropic Equation of State
が成り立っていると仮定した状態方程式です。
Γiは断熱指数と呼ばれ、星の硬さを表す目安になります。 また、星の典型的な大きさはKiの値によって決まります。
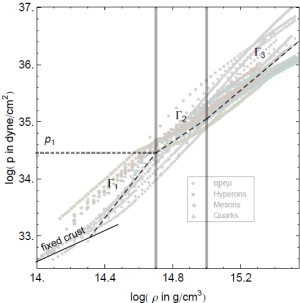
2つの図を重ねると、PEOSによって高密度物質の状態方程式がよく近似されていることがわかります。 この近似をすることで、より現実的な中性子星の構造を計算することができます。
球対称モデルの計算
状態方程式
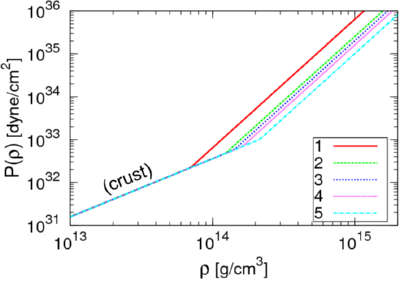
実際の計算においては、図のような5つの状態方程式を与えました。 この図は、横軸を密度、縦軸を圧力にとっています。 状態方程式を変化させると、中性子星の構造には大きな変化が現れます。
圧力・密度分布
重力質量を1.35太陽質量に統一して計算した結果を示します。
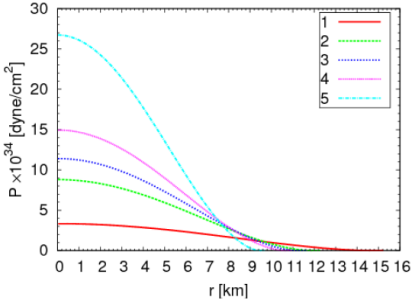
この図は横軸に半径、縦軸に圧力をとり、 中性子星内部でどのように圧力が分布しているかを示したグラフです。 半径r=0の点が中心で、圧力が0になっている部分が それぞれの星の表面と定義します。
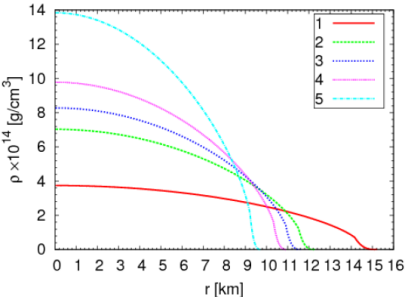
同様に密度の分布を示したのがこの図です。
状態方程式が変わると、密度や圧力の分布の仕方や半径が変化することが確認できます。
解系列
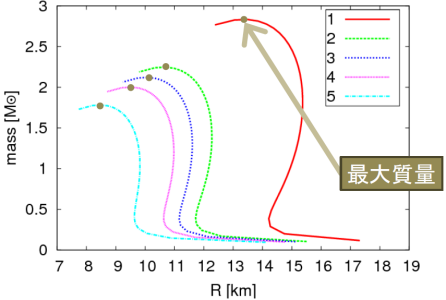
今度は、コンパクトネスと呼ばれる変数、重力質量M/シュワルツシルド半径R を変化させて、 それぞれの半径と質量を計算しました。 図は横軸を半径R、縦軸を重力質量にとっています。
それぞれの頂点が、その状態方程式における最大質量を示しています。 このように、PEOS のパラメータを変化させることで、 最大質量が状態方程式に応じて変化することが再現できました。
回転中性子星の計算
状態方程式
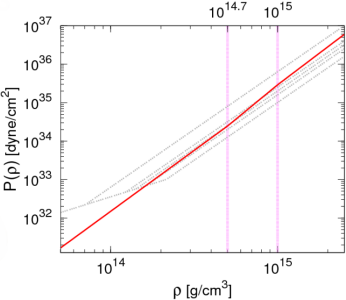
次に、回転している中性子星の計算を、 Akmal-Pandharipande-Ravenhall の提案した高密度物質の状態方程式を近似するパラメータを用いて行いました。 このパラメータは、横軸を密度、縦軸を圧力にとると、 右の図のように表すことができます。 なお、クラストの部分の状態方程式は、簡単のため無視しました。
この計算の結果、中性子星が十分に高速回転すると、その構造は非軸対称になりました。

この図は今回の計算結果ではありませんが、 非軸対称的に変形した中性子星はこのようにラグビーボールのような形になります。
p/ρ分布
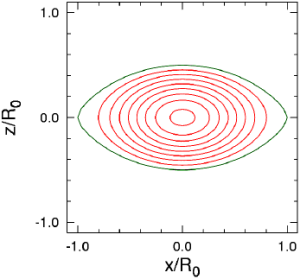
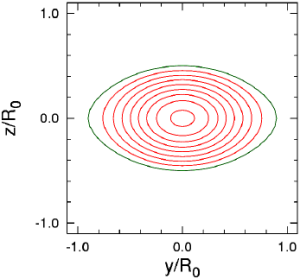
この図は、変形した中性子星をX-Z,Y-Z平面に切って、 その断面でどのようにp/ρが分布しているかをグラフにしたものです。
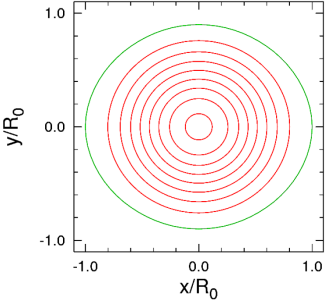
X-Y平面すなわち赤道面では変形しにくいのですが、 よく見るとわずかにY軸方向につぶれているのがわかります。
このように、非軸対称に変形した中性子星からは重力波が放出されます。 そこで四重極公式を用いて重力波を計算しました。