stripe

高温超伝導体におけるストライプ秩序

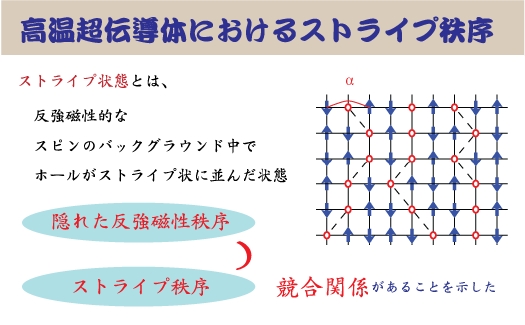
web-fig6.gif

反強磁性長距離秩序状態をもつ絶縁体にホールをドープすることにより高温超伝導が発現することが発見されてから、反強磁性とホールのダイナミクスの関係は広く興味を持たれてきた。本研究では、ホールをドープした磁性体で観測されているストライプ状態に注目し、ストライプを形成するストリングのダイナミクスと反強磁性長距離秩序との関係を調べた。ストライプ状態は反強磁性的なバックグラウンドの中で電荷がストリングを形成し、それらが量子的にゆらいでいる有効模型で記述される。この有効模型を量子モンテカルロシミュレーション(QMC)で詳細に調べることにより、基底状態のスピン長距離秩序と電荷秩序の関係を明らかにした。基底状態の長距離秩序を調べるためには、絶対零度と見なせるほど低温において極めて大きな系のシミュレーションをしなければならない。また、ストリングは各モンテカルロステップで局所的にしか更新されないため、大きなモンテカルロステップ数を必要とする。このため、計算は極めて大規模なものとなる。本研究では、QMCにおいて超並列計算機を用いた計算を行うことにより、基底状態の長距離秩序を詳細に評価できた。ホールの運動エネルギー t を増加させると、ある臨界値で隠れたスピン長距離秩序をもつ相が誘起し、そのオーダーパラメータの値はホールを介したスピン間有効相互作用に起因して増加する。一方、ストライプ秩序のオーダーパラメータは小さくなる。この隠れたスピン長距離秩序とストライプ秩序はコンシステントな位相を維持している。t をさらに増加させると、ストライプの再形成が起こるため、一旦増加した隠れたスピン秩序パラ−メータは減少しはじめ、ある臨界値で無秩序相へ転移する。

関連論文：

前のテーマLinkIcon　　　　　　　　　　　　　　　 ▲　ページトップへ 　　　　　　　　　　　　　　　LinkIcon次のテーマ