| (5.5) |
| (5.6) |
 (「エッチバー」と読む)=[h/2π]と書くことにする。
(「エッチバー」と読む)=[h/2π]と書くことにする。
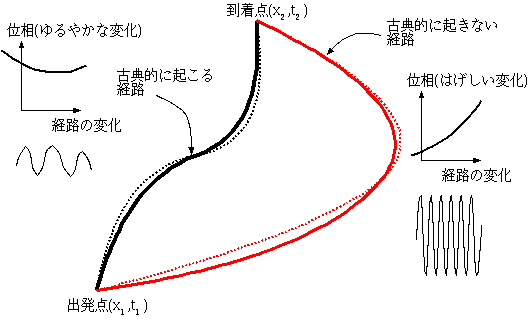
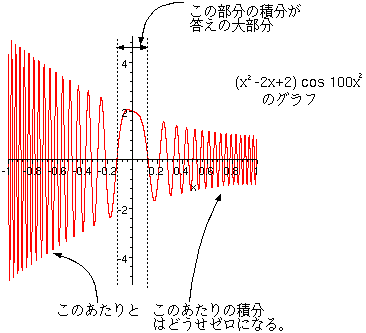 この波の重なる様子を具体的に考えるのは難しいので、だいたいのところどういう状況なのかを理解するために、簡単な積分の場合で変化のゆるやかな部分だけが生き残る例を示しておく。右のグラフは(x2−2x+2)cos100x2のグラフである。この関数は、x=0付近以外では非常に激しく振動している(位相が100x2という式であることを考えればわかる)。この積分を行うと、ほとんどx=0付近だけの積分と同じになる。つまり、x=0
付近以外の寄与は、結果にまったくといっていいほど影響されないのである。これと同様のことが、波動力学における波の重ね合わせでも起きている。ゆえに位
相が極値となるような経路(古典力学的にはEuler-Lagrange方程式の解となっているような経路)が主要な波の経路であると考えてよい。古典力
学と波動力学はこのようにつながる。
ド・ブロイが物質波というものを考えた背景には光学がある。光学においても幾何光学という
立場と、波動光学という立場がある。幾何光学では「光線」を考え、光線がどのように進んでいくかを計算する。一方波動光学では「波」を考え、空間の各点各
点に発生する波の重ね合わせによって波の運動を計算する。この二つのどちらを使っても光がどのように進行するかを考えることができる。
波動(光など)がどのように進行するかは、フェルマーの原理で考える(幾何光学)こともで
きるし、波の重ね合わせを使って考える(波動光学)こともできる。考えているスケールに比べて波長が短い場合(日常現象における可視光の場合など)は幾何
光学を使う方が簡単である。 逆に考えているスケールに比べ波長がcomparable30であるか大きい場合は、波動光学を使わねばならない。
力学でも粒子の進行を、最小作用の原理を使って考えることができる。最小作用の原理に対応するのがフェルマーの原理すなわち幾何光学である。では波動光
学に対応するものは何か???-ド・ブロイはこのような考え方から物質の波動説に到達し、自身のこの考え方を「波動力学」と呼んだ。
この波の重なる様子を具体的に考えるのは難しいので、だいたいのところどういう状況なのかを理解するために、簡単な積分の場合で変化のゆるやかな部分だけが生き残る例を示しておく。右のグラフは(x2−2x+2)cos100x2のグラフである。この関数は、x=0付近以外では非常に激しく振動している(位相が100x2という式であることを考えればわかる)。この積分を行うと、ほとんどx=0付近だけの積分と同じになる。つまり、x=0
付近以外の寄与は、結果にまったくといっていいほど影響されないのである。これと同様のことが、波動力学における波の重ね合わせでも起きている。ゆえに位
相が極値となるような経路(古典力学的にはEuler-Lagrange方程式の解となっているような経路)が主要な波の経路であると考えてよい。古典力
学と波動力学はこのようにつながる。
ド・ブロイが物質波というものを考えた背景には光学がある。光学においても幾何光学という
立場と、波動光学という立場がある。幾何光学では「光線」を考え、光線がどのように進んでいくかを計算する。一方波動光学では「波」を考え、空間の各点各
点に発生する波の重ね合わせによって波の運動を計算する。この二つのどちらを使っても光がどのように進行するかを考えることができる。
波動(光など)がどのように進行するかは、フェルマーの原理で考える(幾何光学)こともで
きるし、波の重ね合わせを使って考える(波動光学)こともできる。考えているスケールに比べて波長が短い場合(日常現象における可視光の場合など)は幾何
光学を使う方が簡単である。 逆に考えているスケールに比べ波長がcomparable30であるか大きい場合は、波動光学を使わねばならない。
力学でも粒子の進行を、最小作用の原理を使って考えることができる。最小作用の原理に対応するのがフェルマーの原理すなわち幾何光学である。では波動光
学に対応するものは何か???-ド・ブロイはこのような考え方から物質の波動説に到達し、自身のこの考え方を「波動力学」と呼んだ。
波長が短い場合 波長が長い場合 光学の世界 幾何光学
(フェルマーの原理)
波動光学 力学の世界 古典力学
(最小作用の原理)
波動力学
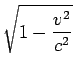 (相対論におけるローレンツ短縮の因子)などという量は1としか実感できない。
我々は量子力学を実感するには大きすぎ、相対論を実感するには小さすぎる。別の言い方をすれば、我々にとってプランク定数hは小さすぎるし、光速度cは速すぎる。だから我々の"常識"は古典力学やニュートン力学を「正しい」と感じてしまう。しかし、だまされてはいけないのである。
ド・ブロイもボーアもアインシュタインも、狭い知見で作られた"常識"から離れて大きな視点を持つことができたからこそ、この世界の真実を知ることができた。21世紀に生きる我々も、思考を柔軟にして量子力学を学んでいこう。
(相対論におけるローレンツ短縮の因子)などという量は1としか実感できない。
我々は量子力学を実感するには大きすぎ、相対論を実感するには小さすぎる。別の言い方をすれば、我々にとってプランク定数hは小さすぎるし、光速度cは速すぎる。だから我々の"常識"は古典力学やニュートン力学を「正しい」と感じてしまう。しかし、だまされてはいけないのである。
ド・ブロイもボーアもアインシュタインも、狭い知見で作られた"常識"から離れて大きな視点を持つことができたからこそ、この世界の真実を知ることができた。21世紀に生きる我々も、思考を柔軟にして量子力学を学んでいこう。