| − |  2 2
2m |
|
∂2
∂x2 |
ψ = i |
∂
∂t |
ψ |
 前節で
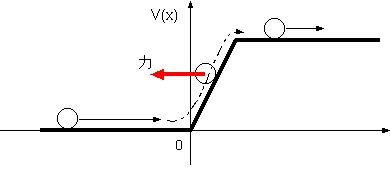
考えたのは、粒子が箱の中に閉じ込められている場合であった。そこでは「境界より外では波動関数が0になる」と考えたが、これはつまりそこに「無限の位置
エネルギーの、越えられない壁」があって、波動関数がそちらに侵入できないのだと考えられる。別の言い方をすれば、「壁」の部分では粒子に無限の大きさの
力が一瞬働いて、方向を変えてしまったと考えよう。
「壁にぶつかったから跳ね返っただけのことじゃないんですか、なんでポテンシャルなんて出て
くるんですか?」と疑問に思う人が時々いるが、そもそも「壁にぶつかったから跳ね返る」という現象が起こるのだってそこにポテンシャルがあるからなのであ
る。今は量子力学をやっていることを忘れずに。たとえば陽子と陽子が衝突する時、実際に粒子どうしが接触したりはしない。実際にぶつかるよりもずっと前に
クーロン力による反発で跳ね返る。また別の考え方をすると、粒子に力が働いて跳ね返るわけだが、その力が保存力であると仮定したら、力が働く場所にはポテ
ンシャルに傾斜があるということになる(図参照)。
前節で
考えたのは、粒子が箱の中に閉じ込められている場合であった。そこでは「境界より外では波動関数が0になる」と考えたが、これはつまりそこに「無限の位置
エネルギーの、越えられない壁」があって、波動関数がそちらに侵入できないのだと考えられる。別の言い方をすれば、「壁」の部分では粒子に無限の大きさの
力が一瞬働いて、方向を変えてしまったと考えよう。
「壁にぶつかったから跳ね返っただけのことじゃないんですか、なんでポテンシャルなんて出て
くるんですか?」と疑問に思う人が時々いるが、そもそも「壁にぶつかったから跳ね返る」という現象が起こるのだってそこにポテンシャルがあるからなのであ
る。今は量子力学をやっていることを忘れずに。たとえば陽子と陽子が衝突する時、実際に粒子どうしが接触したりはしない。実際にぶつかるよりもずっと前に
クーロン力による反発で跳ね返る。また別の考え方をすると、粒子に力が働いて跳ね返るわけだが、その力が保存力であると仮定したら、力が働く場所にはポテ
ンシャルに傾斜があるということになる(図参照)。
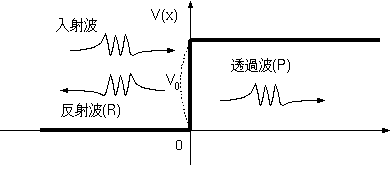 実際に起こる現象としては、おそらく位置エネルギーの差にしろ力にしろ、無限のエネルギー差や無限の力が働くとは考えがたい。そこで以下では、有限の高さ
のポテンシャルの障壁に波があたった時に何が起こるかを考えよう。
ただし、ポテンシャルの変化はある地点で急激に起こるとして計算を簡単にする(傾きを有限にしても解けないわけではないが計算が面倒になる)。結果として
粒子には(古典的に考えれば)一瞬の間に力を受けることになる。その状況を右図のような
実際に起こる現象としては、おそらく位置エネルギーの差にしろ力にしろ、無限のエネルギー差や無限の力が働くとは考えがたい。そこで以下では、有限の高さ
のポテンシャルの障壁に波があたった時に何が起こるかを考えよう。
ただし、ポテンシャルの変化はある地点で急激に起こるとして計算を簡単にする(傾きを有限にしても解けないわけではないが計算が面倒になる)。結果として
粒子には(古典的に考えれば)一瞬の間に力を受けることになる。その状況を右図のような
|
(13.13) |
|
(13.14) |
|
(13.15) |
|
(13.16) |
|
(13.17) |
 2 k2)/2m]=E,[(
2 k2)/2m]=E,[( 2
(k′)2)/2m]=E−V0 である。ここで、x >
0の領域にいるのは、左からやってきた波eikxの
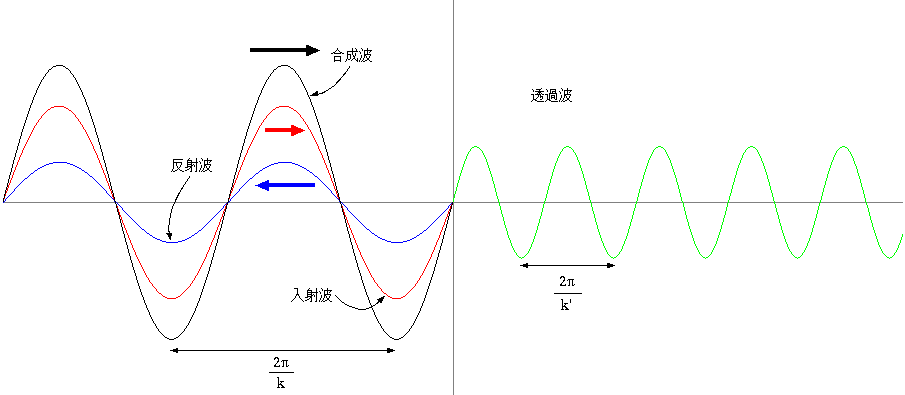
一部が壁を乗り越えてやってきているのだろうから、どれくらい透過したかを示す係数Pをつけて表した。一方x <
0では、壁のところで一部反射して左行きの波ができる可能性があるので、その波がRという係数をもっているとして足し合わせた。P,Rは一般に複素数でよ
いが、その値はx=0における接続で決まる。|P|は透過波の、|R|は反射波の振幅に対応する。
なお、係数を簡単にするために入射波の振幅を1にしたので、この波動関数は規格化されていないことに注意せよ。実際このように無限に拡がった波動関数を
考える時、運動量の固有状態であるeikxを1に規格化することはできない。有限の体積であれば、
2
(k′)2)/2m]=E−V0 である。ここで、x >
0の領域にいるのは、左からやってきた波eikxの
一部が壁を乗り越えてやってきているのだろうから、どれくらい透過したかを示す係数Pをつけて表した。一方x <
0では、壁のところで一部反射して左行きの波ができる可能性があるので、その波がRという係数をもっているとして足し合わせた。P,Rは一般に複素数でよ
いが、その値はx=0における接続で決まる。|P|は透過波の、|R|は反射波の振幅に対応する。
なお、係数を簡単にするために入射波の振幅を1にしたので、この波動関数は規格化されていないことに注意せよ。実際このように無限に拡がった波動関数を
考える時、運動量の固有状態であるeikxを1に規格化することはできない。有限の体積であれば、
|
(13.18) |
|
(13.19) |
|
(13.20) |
|
(13.21) |
|
(13.22) |
|
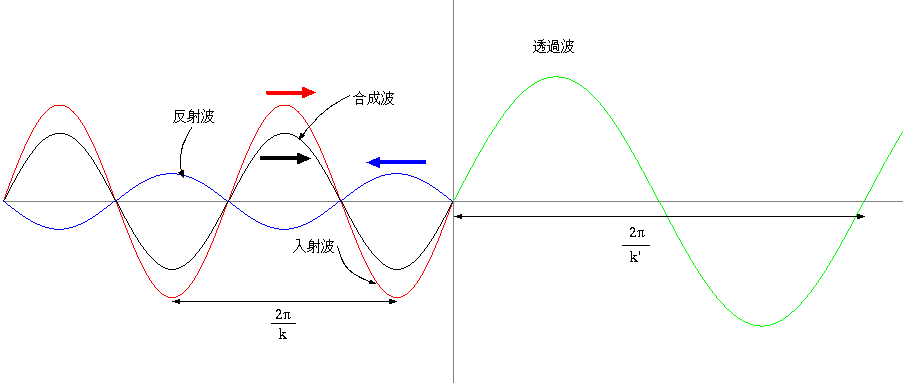
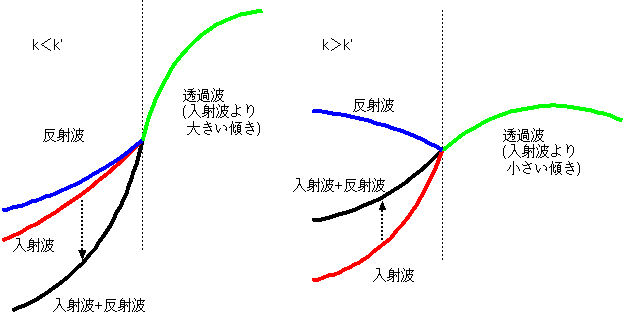 透過波の微係数の絶対値k′P=[2kk′/(k+k′)]は、入射波の傾きの絶対値k
に比べ、k < k′では大きくなり、k > k′では小さくなる。これは、k <
k′では波長が短かくなり、波が圧縮された形になる(当然、傾きは増える)ということの反映である。入射波より透過波の方が傾きが急になっているが、合成
波(入射波+反射波)の傾きは透過波と同じでなくてはならない。そのため、反射波は入射波の傾きを強める波でなくてはならない。k >
k′では逆に傾きを弱めなくてはならない。
もう一つの説明は、k > k′では透過波は入
射波より大きい振幅を持つことを使う。透過波と合成波はつながっているのだから、合成波が境界で強め合っていないと困る。つまり反射波は符号反転せずに足
し算されねばならない(なぜ振幅が大きくなるのかは問い13.2の答えである)。
透過波の微係数の絶対値k′P=[2kk′/(k+k′)]は、入射波の傾きの絶対値k
に比べ、k < k′では大きくなり、k > k′では小さくなる。これは、k <
k′では波長が短かくなり、波が圧縮された形になる(当然、傾きは増える)ということの反映である。入射波より透過波の方が傾きが急になっているが、合成
波(入射波+反射波)の傾きは透過波と同じでなくてはならない。そのため、反射波は入射波の傾きを強める波でなくてはならない。k >
k′では逆に傾きを弱めなくてはならない。
もう一つの説明は、k > k′では透過波は入
射波より大きい振幅を持つことを使う。透過波と合成波はつながっているのだから、合成波が境界で強め合っていないと困る。つまり反射波は符号反転せずに足
し算されねばならない(なぜ振幅が大きくなるのかは問い13.2の答えである)。| 波数の関係 | ポテンシャル | 波長 | 位相速度 | 群速度 | 反射波の位相 | 境界で波は |
| k > k′ | 高い方へ | 長くなる | 速くなる | 遅くなる | ずれない | 強め合う |
| k < k′ | 低い方へ | 短くなる | 遅くなる | 速くなる | πずれる | 弱め合う |
|