|
|
|
|
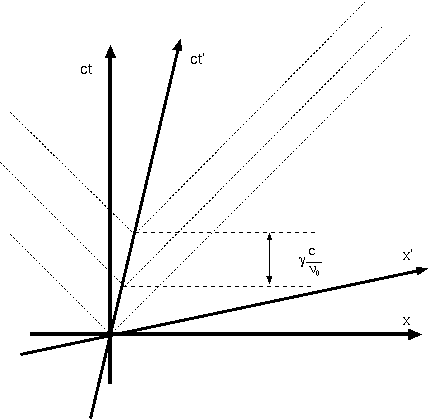
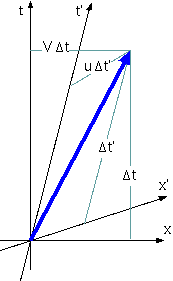 ローレンツ変換(6.9),(6.10)で結ばれた二つの座標系(x,ct)座標と(x′,ct′)座標を考える。x′座標系の原点はx座標系で見ると速度vで運動している。(x′,ct′)座標系で速度uを持っている物体の速度は、(x,t)座標系ではいくらに見えるだろうか。つまり「速度vで動く電車の中で速度uで走る人は、外から見るといくらの速度に見えるか」という問題を考えよう。ガリレイ変換的"常識"ではこれはu+vとなる。
(x′,ct′)座標系で見て速度uで動く物体の軌跡は、x′=ut′で表される。この式を(x,ct)座標系で表せば、x=Vtだったとする。座標変換してみると、
ローレンツ変換(6.9),(6.10)で結ばれた二つの座標系(x,ct)座標と(x′,ct′)座標を考える。x′座標系の原点はx座標系で見ると速度vで運動している。(x′,ct′)座標系で速度uを持っている物体の速度は、(x,t)座標系ではいくらに見えるだろうか。つまり「速度vで動く電車の中で速度uで走る人は、外から見るといくらの速度に見えるか」という問題を考えよう。ガリレイ変換的"常識"ではこれはu+vとなる。
(x′,ct′)座標系で見て速度uで動く物体の軌跡は、x′=ut′で表される。この式を(x,ct)座標系で表せば、x=Vtだったとする。座標変換してみると、
| (7.1) |
| (7.2) |
u+v
|
|
| V= |
0.5c+0.5c
| =0.8c |
| (7.3) |
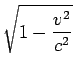 /(1+[(uxv)/(c2)])]ということがわかる。z方向も同様に、uz [
/(1+[(uxv)/(c2)])]ということがわかる。z方向も同様に、uz [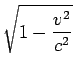 /(1+[(uxv)/(c2)])]とわかる。y,z座標は変化しないが、時間座標が変化しているので、y,z方向の速度が変化する。これもガリレイ変換の場合とは大きく違う。
/(1+[(uxv)/(c2)])]とわかる。y,z座標は変化しないが、時間座標が変化しているので、y,z方向の速度が変化する。これもガリレイ変換の場合とは大きく違う。
| (7.4) |
| (7.5) |
| (7.6) |

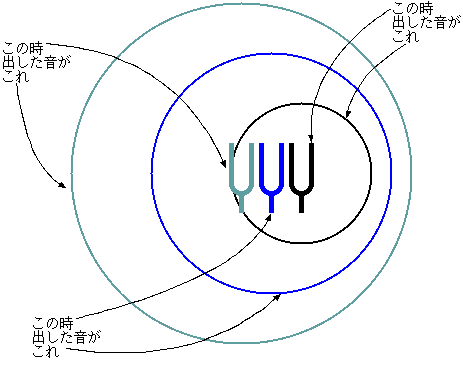 振動数fは波長λと音速Vによって、f=[(V)/λ]と書かれる。1.
は、この式の分母の変化である。図で書けば右のようになる。これは音源が動きながら音を出している様子である。音源が動いても、まわりの空気(音の媒質)
はいっしょに動いているわけではないので、音を出した場所を中心として球状に(図では円状になっている)広がる。音が広がるまでの間に音源が移動している
ので、前方では波がつまり(波長が短くなり)、後方では波が広がる(波長が長くなる)。
これに対して2.は、f=[(V)/λ]の分子の方の変化である。同じ波長の波が来たとしても、自分が波に立ち向かっていくならば、1秒間に遭遇する波の数が増える。逆に波から遠ざかるならば、波の数が減る。
しかしこのような説明を聞いた後で、「さて光の場合のドップラー効果はどうなるのか」と考えると、ちょっと不思議なことに気づくだろう。音の場合、観測者の運動によって音速が変る(7.4の場合)。だから音の振動数が変化するわけである。しかし光の場合、そんなことは起きない(光速度不変の原理!)。では光の場合、「観測者が運動している場合のドップラー効果」は存在しないのか。もちろんそんなことはない。以下で、まず図を書いて考えてみよう。
振動数fは波長λと音速Vによって、f=[(V)/λ]と書かれる。1.
は、この式の分母の変化である。図で書けば右のようになる。これは音源が動きながら音を出している様子である。音源が動いても、まわりの空気(音の媒質)
はいっしょに動いているわけではないので、音を出した場所を中心として球状に(図では円状になっている)広がる。音が広がるまでの間に音源が移動している
ので、前方では波がつまり(波長が短くなり)、後方では波が広がる(波長が長くなる)。
これに対して2.は、f=[(V)/λ]の分子の方の変化である。同じ波長の波が来たとしても、自分が波に立ち向かっていくならば、1秒間に遭遇する波の数が増える。逆に波から遠ざかるならば、波の数が減る。
しかしこのような説明を聞いた後で、「さて光の場合のドップラー効果はどうなるのか」と考えると、ちょっと不思議なことに気づくだろう。音の場合、観測者の運動によって音速が変る(7.4の場合)。だから音の振動数が変化するわけである。しかし光の場合、そんなことは起きない(光速度不変の原理!)。では光の場合、「観測者が運動している場合のドップラー効果」は存在しないのか。もちろんそんなことはない。以下で、まず図を書いて考えてみよう。
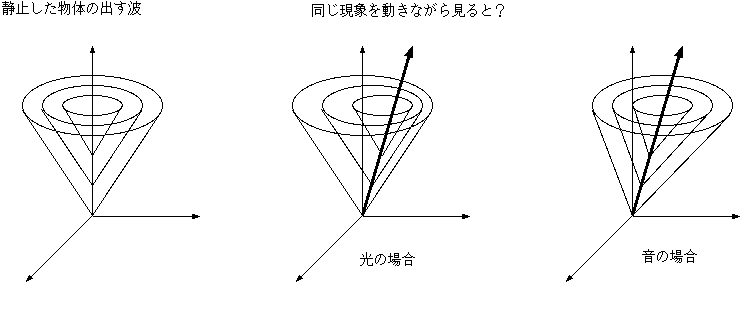
 今考えた二つ(上中、上右図)は同じ現象を動きながら見た場合であった。そのため、音の場合、
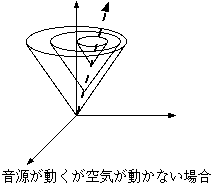
音源と同じ速度で媒質(空気)が動いていた。では空気の中を音源が動くとどうなるかを書いたのが右の図である。この場合、音円錐は傾かないが音源の動きの
せいで波面が同心球にならない。つまりこの場合、波長が変化することで振動数が変化している(音速は変化していない)。
波の振動数νは波長λと波の伝わる速さvで表すとν = [(v)/λ]であるが、音の場合、波源が動いたならばλが変化し、観測者が動いたら音速vが変化する。光の場合、速さvは
変化しないので、変化は全て波長の変化に帰着される。しかし、その波長が変化する理由は実は二つある。一つは図に現れている、波と波の間隔がつまるという
現象である。もう一つ、いわゆるウラシマ効果によって、波源(光源)が波を出してから次に波を出すまでの間隔がのびる。この二つの効果によって光の波長が
変化し、ゆえに振動数が変化するのである。このように、光速度不変(cは観測者の速度によって変化しない)であっても、振動数や波長は観測者の速度によって変化しうる。
では、どのように光のドップラー効果が起こるかを、ローレンツ変換の式を使って計算してみよう。光の振動数(ただし、音源が静止している場合に出す光の振動数)をν0とする。光源の静止系(x′系とする。)では、「山」を出してから次に「山」を出すまでの時間は[1/(ν0)]であるから、光の「山」が出た時空点を(x′,y′,z′,ct′)=(0,0,0,[(nc)/(ν0)])(nは整数)と考えることができる。これをローレンツ変換すると、(x,y,z,ct)=(γβ[(nc)/(ν0)],0,0, γ[(nc)/(ν0)] )となる。つまりこれが光源が動いている座標系において光の「山」が出た時空点である。
今考えた二つ(上中、上右図)は同じ現象を動きながら見た場合であった。そのため、音の場合、
音源と同じ速度で媒質(空気)が動いていた。では空気の中を音源が動くとどうなるかを書いたのが右の図である。この場合、音円錐は傾かないが音源の動きの
せいで波面が同心球にならない。つまりこの場合、波長が変化することで振動数が変化している(音速は変化していない)。
波の振動数νは波長λと波の伝わる速さvで表すとν = [(v)/λ]であるが、音の場合、波源が動いたならばλが変化し、観測者が動いたら音速vが変化する。光の場合、速さvは
変化しないので、変化は全て波長の変化に帰着される。しかし、その波長が変化する理由は実は二つある。一つは図に現れている、波と波の間隔がつまるという
現象である。もう一つ、いわゆるウラシマ効果によって、波源(光源)が波を出してから次に波を出すまでの間隔がのびる。この二つの効果によって光の波長が
変化し、ゆえに振動数が変化するのである。このように、光速度不変(cは観測者の速度によって変化しない)であっても、振動数や波長は観測者の速度によって変化しうる。
では、どのように光のドップラー効果が起こるかを、ローレンツ変換の式を使って計算してみよう。光の振動数(ただし、音源が静止している場合に出す光の振動数)をν0とする。光源の静止系(x′系とする。)では、「山」を出してから次に「山」を出すまでの時間は[1/(ν0)]であるから、光の「山」が出た時空点を(x′,y′,z′,ct′)=(0,0,0,[(nc)/(ν0)])(nは整数)と考えることができる。これをローレンツ変換すると、(x,y,z,ct)=(γβ[(nc)/(ν0)],0,0, γ[(nc)/(ν0)] )となる。つまりこれが光源が動いている座標系において光の「山」が出た時空点である。
| (7.7) |
| (7.8) |
| (7.9) |
| (7.10) |