|
|
dτ dt | = | √ |
| = | 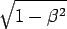 |
|
| (9.3) |
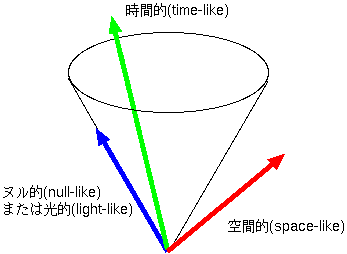 ds2はいろんな符号がありえる。符号によって
ds2はいろんな符号がありえる。符号によって
| (9.4) |
| (9.5) |
| ( |
| ) |
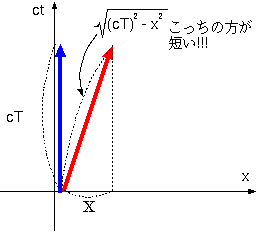 グラフを見ると斜め線の方が長く見えるが、今長さの定義が4次元的距離で定義されていることに気をつけなくてはいけない。そのため、真っ直ぐな線の4次元的距離の自乗は−(cT)2であり、斜め線の4次元的距離の自乗は−(cT)2+X2 となる。「距離の自乗」がマイナスになるのは「自乗」という言葉の本来の意味からすると奇妙であるが、今「距離の自乗」は−(cT)2+x2+y2+z2と定義されているのでこれでよい。本来の意味とは違う使い方をしていることになるが、物理専用の用語なのだと思って納得して欲しい。
マイナスになるのが気になるのであれば、「時間的な距離を測る時には距離の自乗は(cT)2−x2−y2−z2と定義する」と決めておいてもよい。
グラフを見ると斜め線の方が長く見えるが、今長さの定義が4次元的距離で定義されていることに気をつけなくてはいけない。そのため、真っ直ぐな線の4次元的距離の自乗は−(cT)2であり、斜め線の4次元的距離の自乗は−(cT)2+X2 となる。「距離の自乗」がマイナスになるのは「自乗」という言葉の本来の意味からすると奇妙であるが、今「距離の自乗」は−(cT)2+x2+y2+z2と定義されているのでこれでよい。本来の意味とは違う使い方をしていることになるが、物理専用の用語なのだと思って納得して欲しい。
マイナスになるのが気になるのであれば、「時間的な距離を測る時には距離の自乗は(cT)2−x2−y2−z2と定義する」と決めておいてもよい。
| (9.6) |
| (9.7) |
| (9.8) |
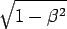 倍である。
固有時は、各物体ごとに違う進み方をする。上の式からわかるように、寄り道をするとdx2が多くなり、結果として固有時の進みは遅れる(ウラシマ効果)。双子のパラドックスの計算なども、運動している物体の固有時が短くなる、と考えれば簡単である。
我々の知っている粒子の世界線はtime-likeであるかnull-likeであるか、ど
ちらかである。世界線がspace-likeだということは超光速で運動している粒子であるということで、そんなものは見つかっていない。もし見つかった
ら、そのような粒子は見る人の立場によっては未来から過去に向かって走ることになるので、因果律に抵触することになるだろう。
世界線がnull-likeになると、固有時の変化dτは0になってしまう。よって光のように光速で動くものに対しては固有時が定義できない(あるいは定義してもそれは変化しない)。
倍である。
固有時は、各物体ごとに違う進み方をする。上の式からわかるように、寄り道をするとdx2が多くなり、結果として固有時の進みは遅れる(ウラシマ効果)。双子のパラドックスの計算なども、運動している物体の固有時が短くなる、と考えれば簡単である。
我々の知っている粒子の世界線はtime-likeであるかnull-likeであるか、ど
ちらかである。世界線がspace-likeだということは超光速で運動している粒子であるということで、そんなものは見つかっていない。もし見つかった
ら、そのような粒子は見る人の立場によっては未来から過去に向かって走ることになるので、因果律に抵触することになるだろう。
世界線がnull-likeになると、固有時の変化dτは0になってしまう。よって光のように光速で動くものに対しては固有時が定義できない(あるいは定義してもそれは変化しない)。
|
| (9.9) |
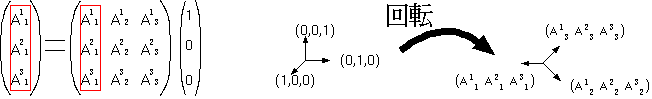
| ( |
| ) |
| (9.10) |
| (9.11) |
| ( |
| ), |
| ( |
| ), |
| ( |
| ) |
| ( |
|
|
| ( |
|
|
| ( |
|
|
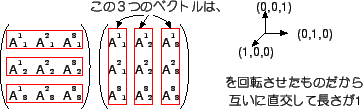
| (9.12) |
| (9.13) |
| (9.14) |
| (9.15) |
| (9.16) |
| (9.17) |
| (9.18) |
| (9.19) |
| (9.20) |
| (9.21) |
| (9.22) |
| (9.23) |
| (9.24) |
ここまでの流れを整理しよう。ここまで、相対性原理(絶対空間は存在しないということ)を一つ の原理として捉えてきた。そして、電磁気の基本法則であるマックスウェル方程式が相対性原理を満たしていないように見える(ガリレイ変換で不変でない)こ とから、マックスウェル方程式を破棄するか、ガリレイ変換を破棄するかの二者択一を迫られることになった。マイケルソン・モーレーをはじめとする実験事実 から、破棄されるべきなのはガリレイ変換であり、ローレンツ変換へと修正すべきであることがわかった。また、時間と空間を別物と考えるのではなく、合わせ て4次元の時空を考えて、その4次元を混ぜ合わせるような変換としてローレンツ変換を捉えればよいことがわかった。 そこでもう一度元にもどって考えると、そもそも相対性原理が考えられたのは、ニュートン力学 はガリレイ変換で不変であったからである。しかし電磁気に対する考察からガリレイ変換はローレンツ変換へと修正されたのだから、今度はニュートン力学を ローレンツ変換で不変になるように作り直さなくてはいけない。この章で考えるのはローレンツ変換で不変になるように作り直された新しい力学、すなわち相対 論的力学である。 そこで、どのようにして相対論的力学を作るか、その概要を述べる。ニュートン力学の基本である運動方程式は
ガリレイ変換 ローレンツ変換 実験的検証 ニュートン力学(非相対論的) ○ × 19世紀まで○ ヘルツの方程式(非相対論的) ○ × × マックスウェル方程式(相対論的) × ○ ○ 相対論的力学? × ○ ○
| (10.1) |
|
∂ ∂xν |