|
|
|
|
| Vμ = | ( | c( |
dt dτ | ) | , | ( |
dx dτ | ) | , | ( |
dy dτ | ) | , | ( |
dz dτ | ) | ) |
| (10.2) |
| (10.3) |
| (10.4) |
| (10.5) |
| (10.6) |
| (10.7) |
| (10.8) |
| (10.9) |
| (10.10) |
| (10.11) |
| (10.12) |
| (10.13) |
| (10.14) |
| (10.15) |
| (10.16) |
| (10.17) |
| (10.18) |
| (10.19) |
| (10.20) |
| (10.21) |
| (10.22) |
| (10.23) |
| (10.24) |
| (10.25) |
| (10.26) |
| (10.27) |
| (10.28) |
| (10.29) |
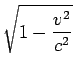 )] となる。非相対論的な計算では分母の
)] となる。非相対論的な計算では分母の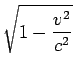 は表れない。実験によって支持されるのはもちろん相対論的な計算であり、荷電粒子を磁場中で加速する(サイクロトロンなど)実験装置ではこのいわゆる「質量増大」の効果を考えて設計せねばならない。
逆に、運動方向と加速度が同じ方向を向いていると、また話が少し変わる。この場合、viも[(dvi)/dt]もx成分だけが零でないとすると、
は表れない。実験によって支持されるのはもちろん相対論的な計算であり、荷電粒子を磁場中で加速する(サイクロトロンなど)実験装置ではこのいわゆる「質量増大」の効果を考えて設計せねばならない。
逆に、運動方向と加速度が同じ方向を向いていると、また話が少し変わる。この場合、viも[(dvi)/dt]もx成分だけが零でないとすると、
| (10.30) |
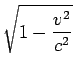 があるのだとした方が簡便である。どちらの流儀でも、「相対論では運動量がmvではなくmvγになる」ということを把握しておけば問題はない。
ここで、fμが有限で時間経過も有限である限り、Pμは有限の値を取ることに注意しよう。速度を増やしていくと、v=cとなったところでPμは無限大となる。ゆえに、有限の力で有限の時間加速している限り、光速に達することはない。このことは光速cが物体の限界速度であることを示している。
があるのだとした方が簡便である。どちらの流儀でも、「相対論では運動量がmvではなくmvγになる」ということを把握しておけば問題はない。
ここで、fμが有限で時間経過も有限である限り、Pμは有限の値を取ることに注意しよう。速度を増やしていくと、v=cとなったところでPμは無限大となる。ゆえに、有限の力で有限の時間加速している限り、光速に達することはない。このことは光速cが物体の限界速度であることを示している。