
| (10.31) |
| (10.32) |
| (10.33) |
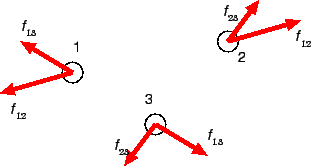
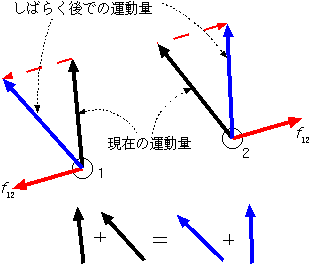 ���ʤ����������Ǥϱ�ư�̤ȥ��ͥ륮����Ʊ��������ư�̤ζ�����ʬ�Ȼ�����ʬ�Ȥ������ˤޤȤޤäƤ���Τǡ���ư�̤�������¸���ƥ��ͥ륮������¸���ʤ��Ȥ������뤤�Ϥ��εդΤ��ȤʤɤϤ������ʤ����㤦��ɸ�Ϥ˰ܤ�л�����ʬ�ȶ�����ʬ�������ʤ��Ȥ��С�P��0=��(P0�ݦ�P1)
�Ȥ����դ��ˡˤΤǡ����Ƥκ�ɸ�ϤDZ�ư����¸§����Ω���뤿��ˤϡ����ͥ륮������¸���Ƥ��Ƥ���ʤ��Ⱥ���ΤǤ��롣�������������������ε���Ǥ�
�롣�˥塼�ȥ��ϳؤǤϡ�������뤫�饨�ͥ륮������¸���ʤ��פȤ��������������줿����������Ū�ϳؤǤ���ˤ�äƼ���줿���ͥ륮��������ȴ�
�ꤷ����¸������ˤʤäƤ��ʤ��ƤϤ����ʤ���
����ǤϺ��ѡ�ȿ���Ѥ�ˡ§����Ω�Ȥ������Ȥ��ꤷ�������������ξ��ˤϤ��β���ˤ�����
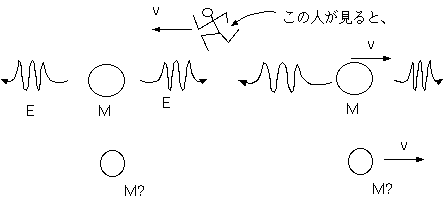
��ɬ�פǤ��롣�ʤ��ʤ顢�������Ǥ϶���Ū��Υ�줿���Ǥ�Ʊ����ˤϰ�̣���ʤ�����οޤǤϡ�Υ�줿ʪ�ΤȤδ֤��Ϥ���Ʊ���ˡ�Ư���Ƥ��뤫�Τ��Ȥ���
���Ƥ��뤬���ºݤˤϤ���ʤ��Ȥϵ����ʤ��ʤ��⤽�⡢�Ϥ��®���®�������Ϥ����ʤ����ˡ��������äƸ�̩�ˤϡ����ѡ�ȿ���Ѥ�ˡ§��ñ���Ŭ�Ѥ���
�褤�Τϡ�ʪ�Τ�ʪ�Τ��ܿ����ơ�Ʊ���������¸�ߤ��ơ��Ϥ�ڤܤ����Ǥ��롣���������Ϥ����Ĥ��Ų٤β����礤�ʰ����礤�ˡפȹͤ����硢����ȿ
���Ѥ�ˡ§����Ω���Ƥ���Ȥϸ¤�ʤ��������������������Ϥ���Ų٤ȡ����ξ����ż���Ȥ���ߺ��Ѥˤ���ϡפȹͤ���ʤ�С������Ⱥ��ѡ�ȿ���Ѥ�
��Ω����Τ��������ξ��ϡ��ż���λ��ı�ư�̡פ�����Ƥ��ʤ��ƤϤ����ʤ���
���ޤ���ʪ�Τ��ܿ����ƾ��ͤ���Ȥ���ñ�������ξ���������Ū�ʾ�����������Ū�ʾ��ˤɤΤ褦�ʺ������뤫���ǧ���Ƥ�������
���ʤ����������Ǥϱ�ư�̤ȥ��ͥ륮����Ʊ��������ư�̤ζ�����ʬ�Ȼ�����ʬ�Ȥ������ˤޤȤޤäƤ���Τǡ���ư�̤�������¸���ƥ��ͥ륮������¸���ʤ��Ȥ������뤤�Ϥ��εդΤ��ȤʤɤϤ������ʤ����㤦��ɸ�Ϥ˰ܤ�л�����ʬ�ȶ�����ʬ�������ʤ��Ȥ��С�P��0=��(P0�ݦ�P1)
�Ȥ����դ��ˡˤΤǡ����Ƥκ�ɸ�ϤDZ�ư����¸§����Ω���뤿��ˤϡ����ͥ륮������¸���Ƥ��Ƥ���ʤ��Ⱥ���ΤǤ��롣�������������������ε���Ǥ�
�롣�˥塼�ȥ��ϳؤǤϡ�������뤫�饨�ͥ륮������¸���ʤ��פȤ��������������줿����������Ū�ϳؤǤ���ˤ�äƼ���줿���ͥ륮��������ȴ�
�ꤷ����¸������ˤʤäƤ��ʤ��ƤϤ����ʤ���
����ǤϺ��ѡ�ȿ���Ѥ�ˡ§����Ω�Ȥ������Ȥ��ꤷ�������������ξ��ˤϤ��β���ˤ�����
��ɬ�פǤ��롣�ʤ��ʤ顢�������Ǥ϶���Ū��Υ�줿���Ǥ�Ʊ����ˤϰ�̣���ʤ�����οޤǤϡ�Υ�줿ʪ�ΤȤδ֤��Ϥ���Ʊ���ˡ�Ư���Ƥ��뤫�Τ��Ȥ���
���Ƥ��뤬���ºݤˤϤ���ʤ��Ȥϵ����ʤ��ʤ��⤽�⡢�Ϥ��®���®�������Ϥ����ʤ����ˡ��������äƸ�̩�ˤϡ����ѡ�ȿ���Ѥ�ˡ§��ñ���Ŭ�Ѥ���
�褤�Τϡ�ʪ�Τ�ʪ�Τ��ܿ����ơ�Ʊ���������¸�ߤ��ơ��Ϥ�ڤܤ����Ǥ��롣���������Ϥ����Ĥ��Ų٤β����礤�ʰ����礤�ˡפȹͤ����硢����ȿ
���Ѥ�ˡ§����Ω���Ƥ���Ȥϸ¤�ʤ��������������������Ϥ���Ų٤ȡ����ξ����ż���Ȥ���ߺ��Ѥˤ���ϡפȹͤ���ʤ�С������Ⱥ��ѡ�ȿ���Ѥ�
��Ω����Τ��������ξ��ϡ��ż���λ��ı�ư�̡פ�����Ƥ��ʤ��ƤϤ����ʤ���
���ޤ���ʪ�Τ��ܿ����ƾ��ͤ���Ȥ���ñ�������ξ���������Ū�ʾ�����������Ū�ʾ��ˤɤΤ褦�ʺ������뤫���ǧ���Ƥ�������
| (10.34) |
| (10.35) |
| (10.36) |
| (10.37) |
| (10.38) |
| (10.39) |
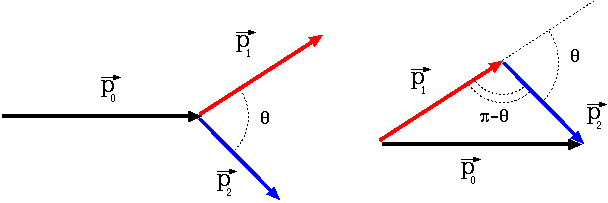
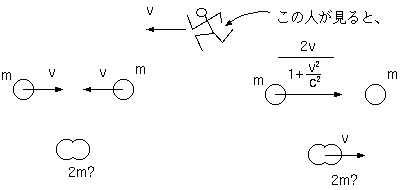
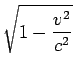 ]��1����礭�����顢����μ��̤�2m����礭���ʤäƤ��뤳�Ȥˤʤ롣
�����ʤ뤳�Ȥ�������Ū�˹ͤ����ɬ���Ǥ��뤳�Ȥ��ǧ���褦�������������ˤ�ꡢƱ�����ݤ�®�١���v����äƱ�ư���Ƥ����¬�Ԥ������Ȥ��Ƥ�Ʊ�����Ȥ������Ǥ��ͤФʤ�ʤ������λ���®�٤ι���§��Ȥ�ͤФʤ�ʤ��Τǡ�®�١���v��ư���ʤ���®����v��ʪ�Τ�����®�٤ϡ�2v�ǤϤʤ���[2v/(1+[(v2)/(c2)])]�Ǥ��뤳�Ȥ����դ��衣����®�٤��б�����äϡ�
]��1����礭�����顢����μ��̤�2m����礭���ʤäƤ��뤳�Ȥˤʤ롣
�����ʤ뤳�Ȥ�������Ū�˹ͤ����ɬ���Ǥ��뤳�Ȥ��ǧ���褦�������������ˤ�ꡢƱ�����ݤ�®�١���v����äƱ�ư���Ƥ����¬�Ԥ������Ȥ��Ƥ�Ʊ�����Ȥ������Ǥ��ͤФʤ�ʤ������λ���®�٤ι���§��Ȥ�ͤФʤ�ʤ��Τǡ�®�١���v��ư���ʤ���®����v��ʪ�Τ�����®�٤ϡ�2v�ǤϤʤ���[2v/(1+[(v2)/(c2)])]�Ǥ��뤳�Ȥ����դ��衣����®�٤��б�����äϡ�
| (10.40) |
| (10.41) |
| (10.42) |
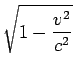 ]=M�Ƚȡ�
]=M�Ƚȡ�
| (10.43) |
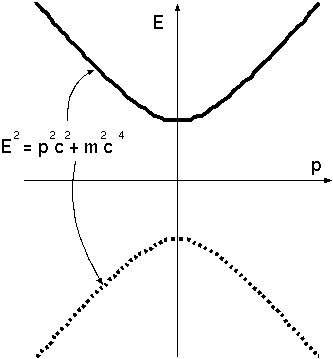
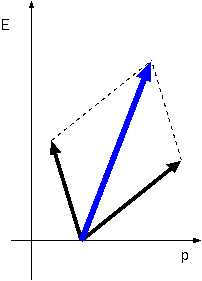
�Ǥ��ꡢ���μ��Ƥ⡢�����ʪ�Τ�M��2E/c2�μ��̤���ä�ʪ�ΤȤ��ƿ������Ȥ��狼 �롣�ʤ��������奿�����μ���Ƴ�����������Υ��ͥ륮���ȱ�ư�̤���ư�ϤǤɤΤ褦�ˤʤ�Τ��ϥ��������Ѵ��ˤ�äƤǤϤʤ����ż�����ˡ§�� ��Ƴ���Ƥ��롣�����奿����Ϥ��Τ褦�ʹͻ����顢�ɤ�ʷ��Ǥ��쥨�ͥ륮�������ͤ����Ȥ���ʪ�Τμ��̤�E/c2������������Ǥ������ȷ��������� ��Ʊ�ͤˡ�Ǯ����̤˹����롣Ǯ����ư����Ȥ������Ȥϥߥ����ˤߤ��ʬ�Ҥα�ư���ͥ륮���������Ȥ������ȤǤ��롣N�Ĥ�γ�Ҥ���ʤ�Ϥ�����Ȥ��ơ���γ�Ҥ�����®��PI������äƤ���(I��γ�Ҥ���̤���ź���Ȥ���)�Ȥ���ȡ����ΤȤ��Ƥϭ�I P��I�Σ�����ư�̤���Ĥ��Ȥˤʤ롣����N�Ĥ�γ�Ҥ�Ȣ���Ĥ������줿���Τ��Ȥ��ơ�Ȣ���Ż߷ϤǸ���б�ư�̤���I PiI=0�Ȥʤ�����ΤȤ��Ƶ��Τ�ư���Ƥʤ��Τ�����ˡ���������I P0I�Ϥ������0�ǤϤʤ���ñ�ʤ��Żߥ��ͥ륮������I mI c2����礭���ʤ�(P0I = mc/
�Ż߷� ��ư��
���ͥ륮�� ��ư�� ���ͥ륮�� ��ư�� ʪ�� Mc2 0 Mc2�� MV�� ��1 E E/c ��(E��VE/c) ��(E/c��VE/c2) ��2 E ��E/c ��(E+VE/c) ��(��E/c��VE/c2) �����ʪ�� Mc2��2E 0 (Mc2��2E)�� (M��2E/c2)V��
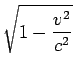 )���ĤޤꡢȢ�����ä����ΤΤ褦�ˡ��ġ��ι���γ�Ҥϱ�ư���Ƥ��뤬���ΤȤ��Ƥ��Żߤ��Ƥ���褦��ʪ�Τμ��̤ϡ����α�ư���ͥ륮�����б�����ʬ�������礭���ʤ�ΤǤ��롣
��E=mc2�Ȥ������ϸ����ϤʤɤǤΤߥ����������åפ���뤳�Ȥ�¿�����������������ͭ�Τ�ΤǤϤʤ������ƤΥ��ͥ륮������Ω����ȹͤ����롣���Ȥ��п��ӽ̤ߤ����Фͤϡ�����Ĺ�ΥХͤ��[(1/2kx2)/(c2)]�������̤��礭���Ǥ������Ȼפ��롣���������Τ褦������Ū�ʥ�٥�Ǥ�c=3��108�Ȥ����������礭���Τ���ˡ���¬��ǽ�ʤۤɤκ��ˤϤʤ�ʤ���
���¤�E=mc2�Ȥ������ϡ������奿����ä���ΤǤ�ʤ���
�С��������ˤ�äƻϤ��Ƴ���줿��ΤǤ�ʤ��������ż�����Ū�ʷ����顢�ŻҤΤ褦�ʲ���γ�Ҥ�ư���������ʴ�������������ˤ��������ž��
���ͥ륮����ʬ���������뤳�Ȥ��ż�����ˡ§����Ƴ����Ƥ�������ñ�˸����ȡ��ŻҤ�ư�������Ȥ���ȡ������ž��ư�����ʤ��ƤϤ����ʤ�������������
����ŻҤ�����Ʊ���褦�˻���Ū���Ѳ����뤳�ȤϤǤ������ž���Ѳ����ŻҤα�ư�ˡ������٤�뤳�Ȥˤʤ롣�����٤줿�ž���ŻҤ��®�ȵ������ˤҤä�
��ΤǤ��롣
���ŻҤ��®���뤿��ˤϡ������Ϥ�ʬ����;�פ��Ϥ�ɬ�פˤʤ롣���줬����������ŻҤμ�����ż������̤���äƤ���פ��Τ褦�˺��Ѥ���ΤǤ��롣�ݥ����������Ĥη��ˤ�ꡢ���μ��̤��ż���Υ��ͥ륮�������㤷������[m/
)���ĤޤꡢȢ�����ä����ΤΤ褦�ˡ��ġ��ι���γ�Ҥϱ�ư���Ƥ��뤬���ΤȤ��Ƥ��Żߤ��Ƥ���褦��ʪ�Τμ��̤ϡ����α�ư���ͥ륮�����б�����ʬ�������礭���ʤ�ΤǤ��롣
��E=mc2�Ȥ������ϸ����ϤʤɤǤΤߥ����������åפ���뤳�Ȥ�¿�����������������ͭ�Τ�ΤǤϤʤ������ƤΥ��ͥ륮������Ω����ȹͤ����롣���Ȥ��п��ӽ̤ߤ����Фͤϡ�����Ĺ�ΥХͤ��[(1/2kx2)/(c2)]�������̤��礭���Ǥ������Ȼפ��롣���������Τ褦������Ū�ʥ�٥�Ǥ�c=3��108�Ȥ����������礭���Τ���ˡ���¬��ǽ�ʤۤɤκ��ˤϤʤ�ʤ���
���¤�E=mc2�Ȥ������ϡ������奿����ä���ΤǤ�ʤ���
�С��������ˤ�äƻϤ��Ƴ���줿��ΤǤ�ʤ��������ż�����Ū�ʷ����顢�ŻҤΤ褦�ʲ���γ�Ҥ�ư���������ʴ�������������ˤ��������ž��
���ͥ륮����ʬ���������뤳�Ȥ��ż�����ˡ§����Ƴ����Ƥ�������ñ�˸����ȡ��ŻҤ�ư�������Ȥ���ȡ������ž��ư�����ʤ��ƤϤ����ʤ�������������
����ŻҤ�����Ʊ���褦�˻���Ū���Ѳ����뤳�ȤϤǤ������ž���Ѳ����ŻҤα�ư�ˡ������٤�뤳�Ȥˤʤ롣�����٤줿�ž���ŻҤ��®�ȵ������ˤҤä�
��ΤǤ��롣
���ŻҤ��®���뤿��ˤϡ������Ϥ�ʬ����;�פ��Ϥ�ɬ�פˤʤ롣���줬����������ŻҤμ�����ż������̤���äƤ���פ��Τ褦�˺��Ѥ���ΤǤ��롣�ݥ����������Ĥη��ˤ�ꡢ���μ��̤��ż���Υ��ͥ륮�������㤷������[m/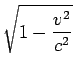 ]
��Ʊ��®�ٰ�¸������Ĥ��Ȥ������Ƥ����ΤǤ��롣
�����������Ǥϡ��ż�Ū�ʥ��ͥ륮�����Ȥ�����̰ʳ����Ф��Ƥ�Ʊ��������Ω���뤫�ɤ����ϡ��¸����Ƥߤʤ��Ȥ狼��ʤ�������������������
�����Ф�����������ͤ���ȡ������Ǥ��뤳�Ȥ���äȤ�餷����������Ū�ˤϼ����ʷ����Ǥ���ˤȤ������Ȥ�������ΤߤǤ��롣�����ˤ⡢�¸��Ϥ�����
�����Ƥ��롣
�����Ȥ��Хإꥦ��42He�ʣ��Ĥ��ۻҡ����Ĥ������ҡ����Ĥ��ŻҤ���ʤ�ˤμ��̤�4.0026032497u�ʸ��Ҽ���ñ�̡ˤǤ��äơ��ſ��ǡʣ��Ĥ��ۻҡ����Ĥ������ҡ����Ĥ��ŻҤ��ʤ�ˤμ���2.01410177779u�Σ��ܤ�꾯���ڤ������⤽�⸶�Ҽ���ñ�̤�126C �μ��̤�12u�Ȥ����������Ƥ��뤬������11H
�μ��̤�1.0078250319u�Ǥ��롣���Τ褦�˸��ҤϹ������ǤǤ����ۻҤ������Ҥμ��̤��¤��ä���Τ���ڤ��ʤ롣�������̷�»�ȸƤӡ�
���θ����ϸ��Ҥ��������ˡ������ʤɤΤ��ޤ��ޤʷ��ǥ��ͥ륮�������Ф���뤳�ȤǤ��롣Ŵ�ʤɡ�����ɽ�ǿ����椢����ˤ��븵�Ǥϼ��̷�»�γ�礬
��äȤ��礭��������ʬ����Ǥ��ꡢ�����ʤɤ��ʬ��������ȥ��ͥ륮������������ͳ�Ϥ���Ǥ��롣
���ݥ����������Ĥ�������Ū���Ϥ���äƷ������櫓�ǤϤʤ��ä��Τˡ����Τ褦�ʷ�
�̤��Ф�������������϶ä��ˤϤ�����ʤ����������Ϥ��⤽�⡢�ż����ءʤ��뤤�ϥޥå����������������ˤ�º�Ť��뤳�Ȥˤ�ä����ޤ줿��ΤǤ��롣��
����ޥå����������������ˤ������ä������������¹Ԥ���С�������Ū�ˤ���������̤��Ф�Τ������ʤΤǤ��롣�ü��������������ޥå���������������
�ˤ�äƵ��Ҥ�����ż����ؤ�������ȯŸ������������ޤ줿��ΤǤ��뤳�Ȥ����λ��¤����狼�롣�ष��������������ä��ż����ؤ����뤹��ȸ��äƤ�
�褤��
]
��Ʊ��®�ٰ�¸������Ĥ��Ȥ������Ƥ����ΤǤ��롣
�����������Ǥϡ��ż�Ū�ʥ��ͥ륮�����Ȥ�����̰ʳ����Ф��Ƥ�Ʊ��������Ω���뤫�ɤ����ϡ��¸����Ƥߤʤ��Ȥ狼��ʤ�������������������
�����Ф�����������ͤ���ȡ������Ǥ��뤳�Ȥ���äȤ�餷����������Ū�ˤϼ����ʷ����Ǥ���ˤȤ������Ȥ�������ΤߤǤ��롣�����ˤ⡢�¸��Ϥ�����
�����Ƥ��롣
�����Ȥ��Хإꥦ��42He�ʣ��Ĥ��ۻҡ����Ĥ������ҡ����Ĥ��ŻҤ���ʤ�ˤμ��̤�4.0026032497u�ʸ��Ҽ���ñ�̡ˤǤ��äơ��ſ��ǡʣ��Ĥ��ۻҡ����Ĥ������ҡ����Ĥ��ŻҤ��ʤ�ˤμ���2.01410177779u�Σ��ܤ�꾯���ڤ������⤽�⸶�Ҽ���ñ�̤�126C �μ��̤�12u�Ȥ����������Ƥ��뤬������11H
�μ��̤�1.0078250319u�Ǥ��롣���Τ褦�˸��ҤϹ������ǤǤ����ۻҤ������Ҥμ��̤��¤��ä���Τ���ڤ��ʤ롣�������̷�»�ȸƤӡ�
���θ����ϸ��Ҥ��������ˡ������ʤɤΤ��ޤ��ޤʷ��ǥ��ͥ륮�������Ф���뤳�ȤǤ��롣Ŵ�ʤɡ�����ɽ�ǿ����椢����ˤ��븵�Ǥϼ��̷�»�γ�礬
��äȤ��礭��������ʬ����Ǥ��ꡢ�����ʤɤ��ʬ��������ȥ��ͥ륮������������ͳ�Ϥ���Ǥ��롣
���ݥ����������Ĥ�������Ū���Ϥ���äƷ������櫓�ǤϤʤ��ä��Τˡ����Τ褦�ʷ�
�̤��Ф�������������϶ä��ˤϤ�����ʤ����������Ϥ��⤽�⡢�ż����ءʤ��뤤�ϥޥå����������������ˤ�º�Ť��뤳�Ȥˤ�ä����ޤ줿��ΤǤ��롣��
����ޥå����������������ˤ������ä������������¹Ԥ���С�������Ū�ˤ���������̤��Ф�Τ������ʤΤǤ��롣�ü��������������ޥå���������������
�ˤ�äƵ��Ҥ�����ż����ؤ�������ȯŸ������������ޤ줿��ΤǤ��뤳�Ȥ����λ��¤����狼�롣�ष��������������ä��ż����ؤ����뤹��ȸ��äƤ�
�褤��