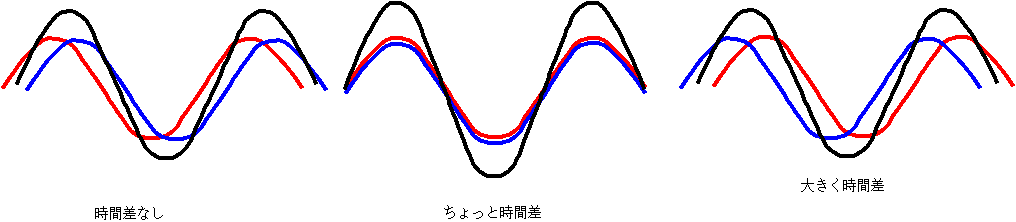

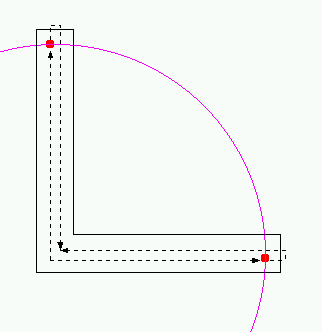
 このあたりの説明は、javaアプレットを使ってアニメーションを見せながら行った。
このあたりの説明は、javaアプレットを使ってアニメーションを見せながら行った。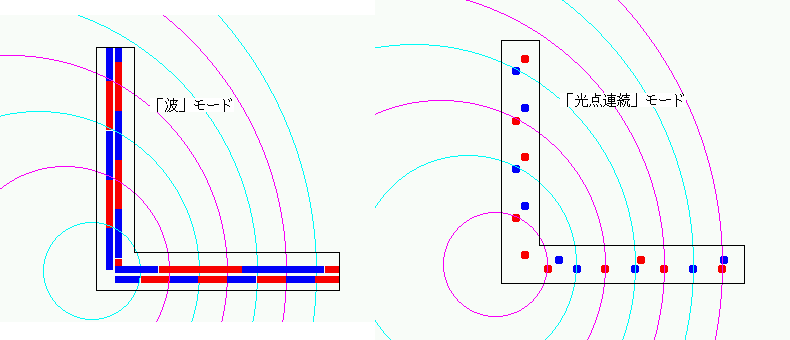
| (5.1) |
|
| (5.4) |
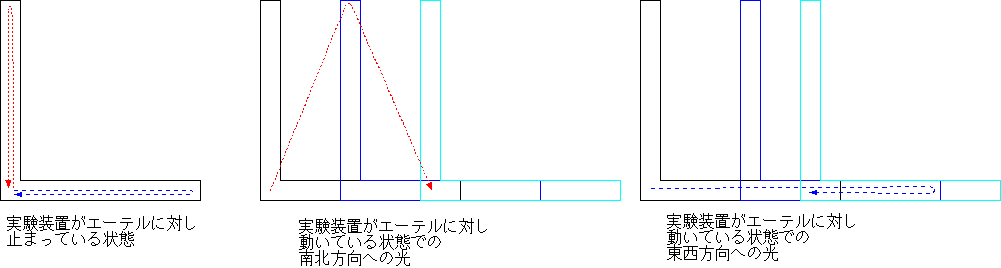
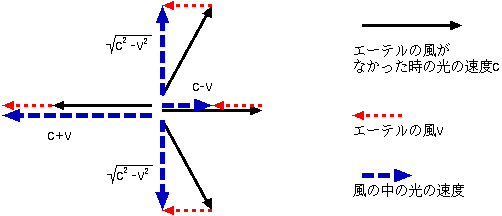 また、エーテルの風と直角の方向(北行きもしくは南行き)の光は、速度が
また、エーテルの風と直角の方向(北行きもしくは南行き)の光は、速度が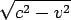 に減る(速さcで斜めに進んだ光が、速さvで東に流されると考えれば、ピタゴラスの定理でこうなることがわかる)。
このように考えると、距離Lを速さc+v,c−v,
に減る(速さcで斜めに進んだ光が、速さvで東に流されると考えれば、ピタゴラスの定理でこうなることがわかる)。
このように考えると、距離Lを速さc+v,c−v,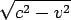 ]でそれぞれ割って足し算するという計算でt東西やt南北が計算できる。結果は同じことになるのはすぐにわかる。
以上、どちらの計算でもt東西とt南北が得られる。そして、この二つには差がある。vはcより十分小さいとして近似を行うと、
]でそれぞれ割って足し算するという計算でt東西やt南北が計算できる。結果は同じことになるのはすぐにわかる。
以上、どちらの計算でもt東西とt南北が得られる。そして、この二つには差がある。vはcより十分小さいとして近似を行うと、
| (5.5) |
| (5.6) |
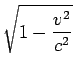 倍違うことから、「東西方向の棒の長さは
倍違うことから、「東西方向の棒の長さは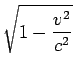 倍に縮んでいる」という説を唱えた。これが古い意味での「ローレンツ短縮」である。フィッツジェラルドも同じようなことを考えていたので「ローレンツ・フィッツジェラルド短縮」と呼ぶこともある。
倍に縮んでいる」という説を唱えた。これが古い意味での「ローレンツ短縮」である。フィッツジェラルドも同じようなことを考えていたので「ローレンツ・フィッツジェラルド短縮」と呼ぶこともある。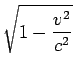 であり、v/cが10−4程度だから、縮む割合は10−8程度となる。そもそも、この精度で長さを測定すること自体が難しいだろう。
本によっては、「ローレンツ短縮」を相対論の帰結である、と説明しているが、ローレンツはあくまで実験を説明するためにad hoc22にこの短縮を導入したのであって、相対論の帰結として理論的に導き出したわけではない。
もう一つ注意しておく。このローレンツ短縮という考え方では、マイケルソン・モーレーの実験について説明することは可能だが、そのほかの実験を説明するに
はこれでは足りない。「ローレンツ変換」はその一部として「ローレンツ短縮」と同様の現象を含んでいるが、より広い意味がある。
「ローレンツ短縮」も「ローレンツ変換」も、アインシュタインではなくローレンツの名前がつ
いている。どちらもアインシュタインより前にローレンツが提出しているからである。しかしローレンツは(同様にこのあたりの研究をしていたポアンカレもそ
うなのだが)「ローレンツ短縮」を、例えば「エーテルの圧力によって物体が縮む」というような、力学的な意味での短縮だと考えていた。「ローレンツ変換」
に関しても「こう考えればうまくいく」という提案であって、その意義を理解してはいない。後で出てくるアインシュタインによる考え方とはその点が違うので
注意すること。
ここでちょっとしゃべっておいたことは「特殊相対論はアインシュタイン一人で作ったというわけではない」ということ。ローレンツやポアンカレはまさに「あ
と一歩」というところまで進めているし、他の物理学者もこの問題をいろいろと考えていた。アインシュタインは特殊相対性原理というきれいなまとめ方で最後
の一歩を担当したことになる。
であり、v/cが10−4程度だから、縮む割合は10−8程度となる。そもそも、この精度で長さを測定すること自体が難しいだろう。
本によっては、「ローレンツ短縮」を相対論の帰結である、と説明しているが、ローレンツはあくまで実験を説明するためにad hoc22にこの短縮を導入したのであって、相対論の帰結として理論的に導き出したわけではない。
もう一つ注意しておく。このローレンツ短縮という考え方では、マイケルソン・モーレーの実験について説明することは可能だが、そのほかの実験を説明するに
はこれでは足りない。「ローレンツ変換」はその一部として「ローレンツ短縮」と同様の現象を含んでいるが、より広い意味がある。
「ローレンツ短縮」も「ローレンツ変換」も、アインシュタインではなくローレンツの名前がつ
いている。どちらもアインシュタインより前にローレンツが提出しているからである。しかしローレンツは(同様にこのあたりの研究をしていたポアンカレもそ
うなのだが)「ローレンツ短縮」を、例えば「エーテルの圧力によって物体が縮む」というような、力学的な意味での短縮だと考えていた。「ローレンツ変換」
に関しても「こう考えればうまくいく」という提案であって、その意義を理解してはいない。後で出てくるアインシュタインによる考え方とはその点が違うので
注意すること。
ここでちょっとしゃべっておいたことは「特殊相対論はアインシュタイン一人で作ったというわけではない」ということ。ローレンツやポアンカレはまさに「あ
と一歩」というところまで進めているし、他の物理学者もこの問題をいろいろと考えていた。アインシュタインは特殊相対性原理というきれいなまとめ方で最後
の一歩を担当したことになる。
|
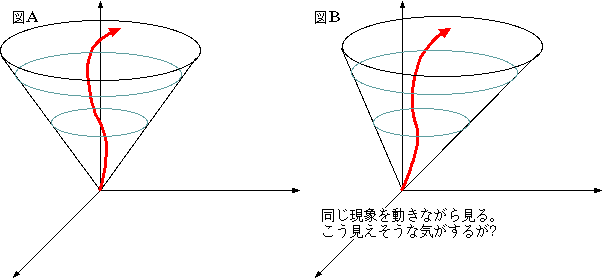
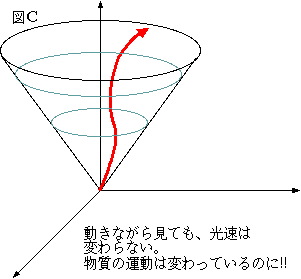 しかし、光の速度は動きながらみても変わらないということが実験事実なので、光円錐の形は変化しないことになる。しかし、物体の運動に関しては変化している(これも実験事実!)。
ちなみに、光の速度は変化しないが、その様子(波長だとか振動数だとか)はいろいろと変わって
いる。どのように変化するのかについては今後の講義で話そう。とにかくここまでで感じて欲しいことは、「図Aを動きながら見たら図Bではなく図Cになると
したら、図Aと図Cはどのような関係になっているのか」ということである。
「動きながら見るということは時々刻々位置が変化していく、ということだから、超平面の位置
がこの図で見て水平方向にずれていくはずだ」という考え方(ガリレイ変換はまさにこういう変換なのである)をすると、どうしても結果は図Bになってしま
う。図Aが図Cに変化するためには、この図の水平方向の動きだけではだめである。かならず「超平面を傾ける」というような操作が必要になる。実際にどんな
操作なのかは以後の講義を聞いてのお楽しみであるが、このような操作がすなわち「4次元的に考える」ということなのである。
しかし、光の速度は動きながらみても変わらないということが実験事実なので、光円錐の形は変化しないことになる。しかし、物体の運動に関しては変化している(これも実験事実!)。
ちなみに、光の速度は変化しないが、その様子(波長だとか振動数だとか)はいろいろと変わって
いる。どのように変化するのかについては今後の講義で話そう。とにかくここまでで感じて欲しいことは、「図Aを動きながら見たら図Bではなく図Cになると
したら、図Aと図Cはどのような関係になっているのか」ということである。
「動きながら見るということは時々刻々位置が変化していく、ということだから、超平面の位置
がこの図で見て水平方向にずれていくはずだ」という考え方(ガリレイ変換はまさにこういう変換なのである)をすると、どうしても結果は図Bになってしま
う。図Aが図Cに変化するためには、この図の水平方向の動きだけではだめである。かならず「超平面を傾ける」というような操作が必要になる。実際にどんな
操作なのかは以後の講義を聞いてのお楽しみであるが、このような操作がすなわち「4次元的に考える」ということなのである。