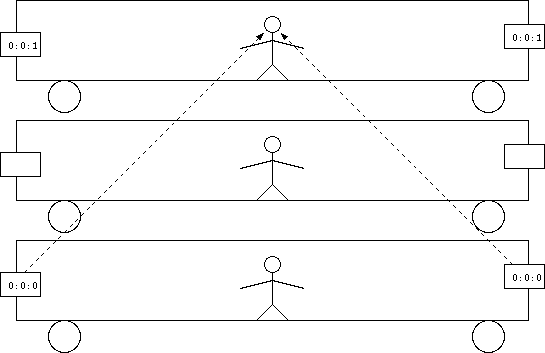

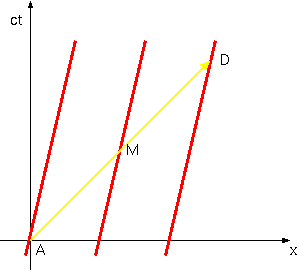
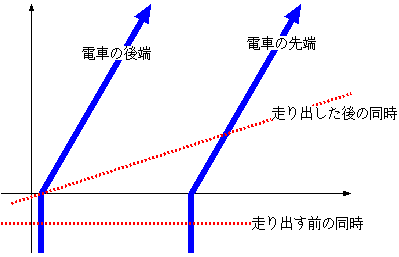
 では次に、どれくらい座標系が傾かなくてはいけないかを作図で示してみよう。
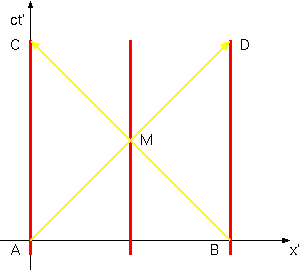
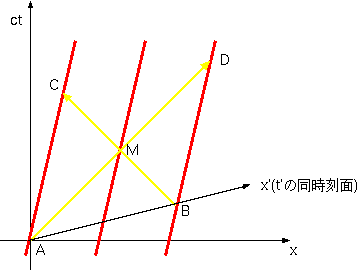
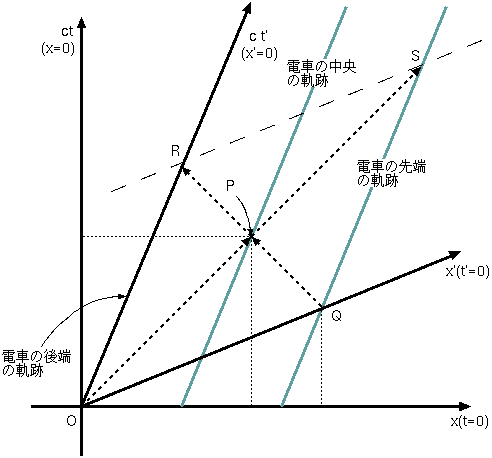
図の(x′,t′)座標系が電車の静止系である。x′=0の線、すなわちt′=
0の線が電車の後端の軌跡に重なるようになっている。光が中央で出会ったのは時空点Mであるとする。電車の前端からも光が出てMに到達したわけだが、前端
から光が出たその瞬間の時空点をBとした。電車の静止系で見ると、前端と後端から光が出た瞬間(AまたはB)は同時刻である。ここで、B→Mと来た光がそ
のまま突き抜けて、後端に達した時空点をCとする。また、A→Mと来た光がそのまま突き抜けて、前端に達した時空点をDとする。ACとBDは、どちらも同
じ電車の一部の運動を表しているので、平行線である。また、ABとCDは、どちらも電車にとっての「同時刻」線であり、電車は一様な運動をしているのだか
ら、平行線である。よってABDCは平行四辺形なのだが、ここでM点でのACとBDの交わりを考える。この二つの線分はどちらも45度の斜め線であるか
ら、直交している。対角線が直交する平行四辺形は菱形である。このことは、このグラフ上におけるx′軸とx 軸の角度が、ct′軸とct軸の角度と等しいことを意味する。つまり、この図はx↔ ctという取り替え(図で言うと、45度線を対称軸とした折り返し)で対称である。
ct′軸状ではx−vt=0が成立するのだから、
では次に、どれくらい座標系が傾かなくてはいけないかを作図で示してみよう。
図の(x′,t′)座標系が電車の静止系である。x′=0の線、すなわちt′=
0の線が電車の後端の軌跡に重なるようになっている。光が中央で出会ったのは時空点Mであるとする。電車の前端からも光が出てMに到達したわけだが、前端
から光が出たその瞬間の時空点をBとした。電車の静止系で見ると、前端と後端から光が出た瞬間(AまたはB)は同時刻である。ここで、B→Mと来た光がそ
のまま突き抜けて、後端に達した時空点をCとする。また、A→Mと来た光がそのまま突き抜けて、前端に達した時空点をDとする。ACとBDは、どちらも同
じ電車の一部の運動を表しているので、平行線である。また、ABとCDは、どちらも電車にとっての「同時刻」線であり、電車は一様な運動をしているのだか
ら、平行線である。よってABDCは平行四辺形なのだが、ここでM点でのACとBDの交わりを考える。この二つの線分はどちらも45度の斜め線であるか
ら、直交している。対角線が直交する平行四辺形は菱形である。このことは、このグラフ上におけるx′軸とx 軸の角度が、ct′軸とct軸の角度と等しいことを意味する。つまり、この図はx↔ ctという取り替え(図で言うと、45度線を対称軸とした折り返し)で対称である。
ct′軸状ではx−vt=0が成立するのだから、
| (6.1) |
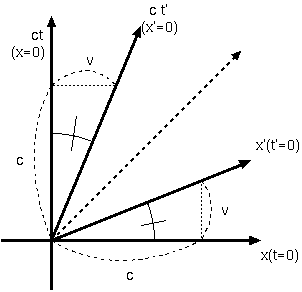
| (6.2) |
| (6.3) |
|
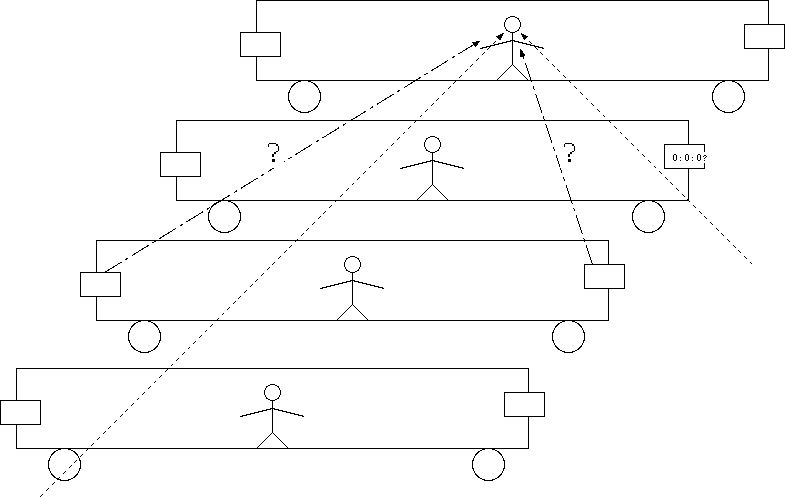
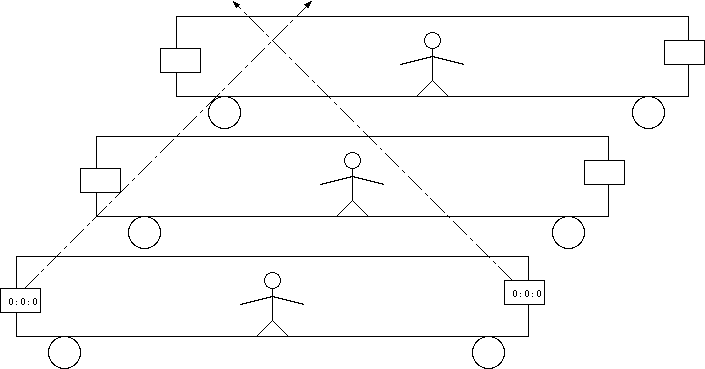
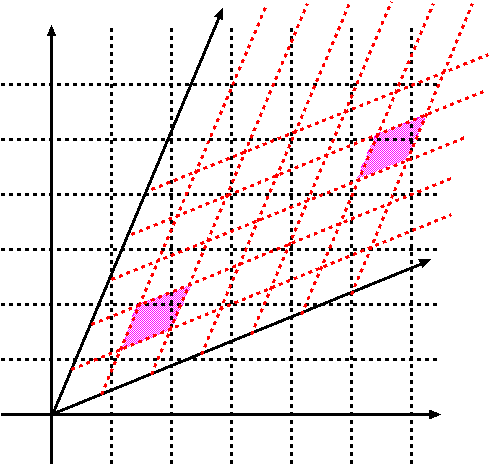 ここで、この座標変換が一次変換に限るということを説明しておく。
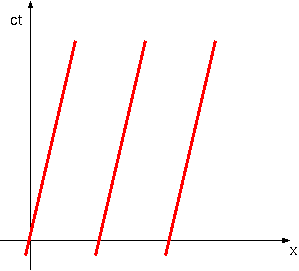
(x,ct)座標系は図のような碁盤の目で表すことができるだろう。これに対して傾いている(x′,ct′)座標系は、やはり傾いた平行四辺形で作られた碁盤の目で表すことができる。(x′,ct′)座標系での碁盤の1マスを塗りつぶして表した。
(x,ct)の関係と(x′,ct′)の関係が1次式でなかったら(たとえば2次式だったりすると)、(x′,ct′)座標系で見た時の碁盤の1マスの大きさが、(x,ct)座標系で見ると一様でない、ということになってしまう。つまりx′座標系での1メートルが、場所によって違う長さでx座標系に翻訳されてしまう。しかし、今考えている座標変換では、x'座標系のどの場所も同じような比率でx座標系と関連づけられているはずである。つまり図で書いたように、違う場所での「(x′,ct′)座標系での1マス」はx座標系で見て同じ大きさ、同じ形のマスになるはずである(これが一様だということ)。そうなるためには、(x,ct)と(x′,ct′)の関係は1次式でなくてはならない。
さらに、どちらの座標系でも光速がcであるということからA=Bであることがわかる。なぜならば、x座標系で原点から右へ進む光の光線上では、x=ctが成立する。この式が成立する時、x′座標系ではx′=ct′ が成立しなくてはおかしい(光速度不変)。(6.4)と(6.5)に、x=ctとx′=ct′を使うと、
ここで、この座標変換が一次変換に限るということを説明しておく。
(x,ct)座標系は図のような碁盤の目で表すことができるだろう。これに対して傾いている(x′,ct′)座標系は、やはり傾いた平行四辺形で作られた碁盤の目で表すことができる。(x′,ct′)座標系での碁盤の1マスを塗りつぶして表した。
(x,ct)の関係と(x′,ct′)の関係が1次式でなかったら(たとえば2次式だったりすると)、(x′,ct′)座標系で見た時の碁盤の1マスの大きさが、(x,ct)座標系で見ると一様でない、ということになってしまう。つまりx′座標系での1メートルが、場所によって違う長さでx座標系に翻訳されてしまう。しかし、今考えている座標変換では、x'座標系のどの場所も同じような比率でx座標系と関連づけられているはずである。つまり図で書いたように、違う場所での「(x′,ct′)座標系での1マス」はx座標系で見て同じ大きさ、同じ形のマスになるはずである(これが一様だということ)。そうなるためには、(x,ct)と(x′,ct′)の関係は1次式でなくてはならない。
さらに、どちらの座標系でも光速がcであるということからA=Bであることがわかる。なぜならば、x座標系で原点から右へ進む光の光線上では、x=ctが成立する。この式が成立する時、x′座標系ではx′=ct′ が成立しなくてはおかしい(光速度不変)。(6.4)と(6.5)に、x=ctとx′=ct′を使うと、
|
|
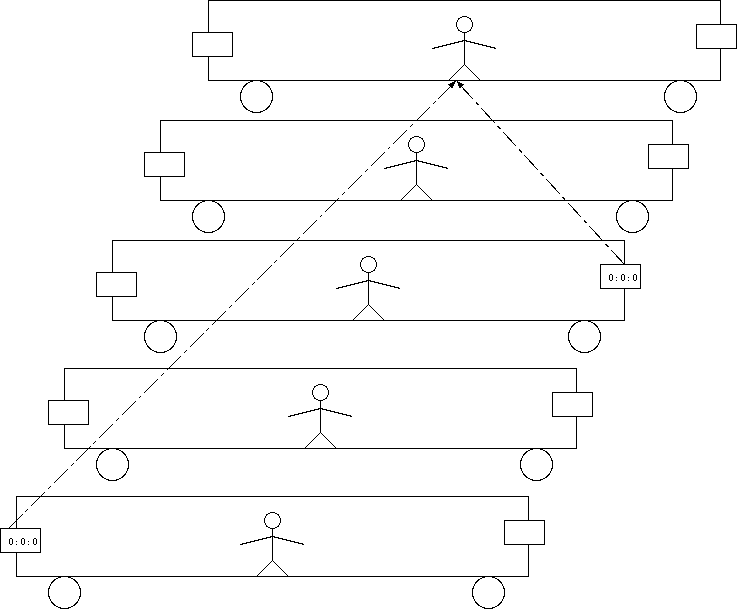
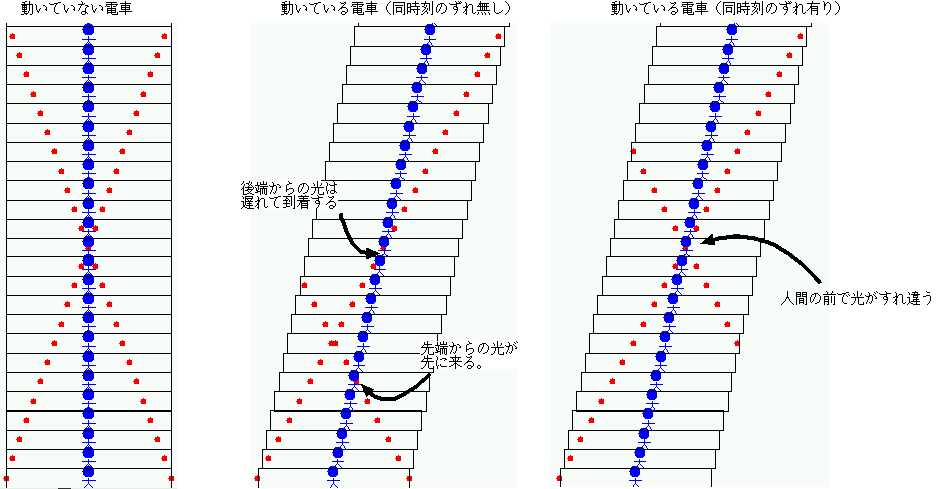
 電車が静止した状態で時計を合わせた後に、電車が光速度の何10%かの速さで動くと、中の人には時計はずれて見えるようになるのですか?
電車が静止した状態で時計を合わせた後に、電車が光速度の何10%かの速さで動くと、中の人には時計はずれて見えるようになるのですか?