|
(9.1) |
|
(9.2) |
|
(9.3) |
|
(9.4) |
 「divが0になるようなベクトルは、別のベクトルのrotで書ける」を証明するには、具体的にそういうベクトルが作れることを示せばよい(面倒ではある
が、少し試行錯誤するとできる)。ここではその逆「何かのベクトルのrotのdivは0である」ということを、図で説明しよう。rotのそもそもの定義
は、微小な面を考えて、その面の回りを回りながらベクトルを線積分した結果を微小面積で割ったものであった。別の言い方をすれば、rot→Aとは、→Aを力と見立て、微小面
積を回る経路で一周した時に→Aのする仕事である。
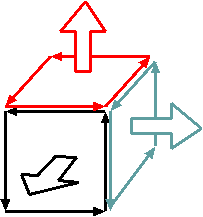
ベクトルのrotで作ったベクトルのdivを作ってみると、左の図のようになる。立方体の各面で、外向きのベクトルに対して右ネジの方向に回りつつその仕
事を計算するのがrot→Aであり、その「外向き」の量を全部足したものがdiv(rot→A)となる。図をよく見ると、矢印が各辺を2回ずつ、逆向きに通っている。この部分で計算される
「仕事」は互いに消し合うので、全部足すと0になる。
「divが0になるようなベクトルは、別のベクトルのrotで書ける」を証明するには、具体的にそういうベクトルが作れることを示せばよい(面倒ではある
が、少し試行錯誤するとできる)。ここではその逆「何かのベクトルのrotのdivは0である」ということを、図で説明しよう。rotのそもそもの定義
は、微小な面を考えて、その面の回りを回りながらベクトルを線積分した結果を微小面積で割ったものであった。別の言い方をすれば、rot→Aとは、→Aを力と見立て、微小面
積を回る経路で一周した時に→Aのする仕事である。
ベクトルのrotで作ったベクトルのdivを作ってみると、左の図のようになる。立方体の各面で、外向きのベクトルに対して右ネジの方向に回りつつその仕
事を計算するのがrot→Aであり、その「外向き」の量を全部足したものがdiv(rot→A)となる。図をよく見ると、矢印が各辺を2回ずつ、逆向きに通っている。この部分で計算される
「仕事」は互いに消し合うので、全部足すと0になる。
|
(9.5) |
|
(9.6) |
|
(9.7) |
|
(9.8) |
|
(9.9) |
|
(9.10) |
|
(9.11) |
|
(9.12) |
|
(9.13) |
|
(9.14) |
|
(9.15) |
|
(9.16) |
|
(9.17) |
|
(9.18) |
|
(9.19) |
|
(9.20) |
|
(9.21) |
|
(9.22) |
|
(9.23) |
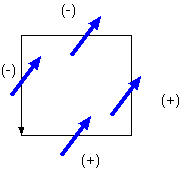 rotについてですが、左の図の符号は正しいですか?
rotについてですが、左の図の符号は正しいですか?