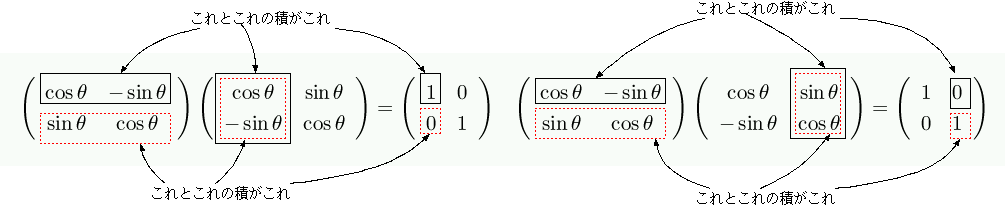
|
|
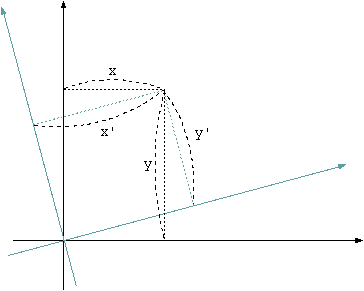 ˇˇ¤·¤«¤·¤ł¤ł¤Ţ¤Ç¤ĎŁ±Ľˇ¸µ¤ÎĎäň˝Ĺ¤Í¤Ć¤¤¤ë¤Ŕ¤±¤ÇĚĚÇňĚŁ¤¬¤Ę¤¤ˇŁŁ˛Ľˇ¸µ¤Ę¤é¤Ç¤Ď¤ÎşÂɸĘŃ´ą¤Ďˇ˘±¦¤ÎżŢ¤Î¤č¤¦¤Ęˇ˘şÂɸĽ´¤Î˛óĹľ¤Ç¤˘¤ëˇŁ
ˇˇ¤·¤«¤·¤ł¤ł¤Ţ¤Ç¤ĎŁ±Ľˇ¸µ¤ÎĎäň˝Ĺ¤Í¤Ć¤¤¤ë¤Ŕ¤±¤ÇĚĚÇňĚŁ¤¬¤Ę¤¤ˇŁŁ˛Ľˇ¸µ¤Ę¤é¤Ç¤Ď¤ÎşÂɸĘŃ´ą¤Ďˇ˘±¦¤ÎżŢ¤Î¤č¤¦¤Ęˇ˘şÂɸĽ´¤Î˛óĹľ¤Ç¤˘¤ëˇŁ
|
(2.11) |
|
|
(2.12) |
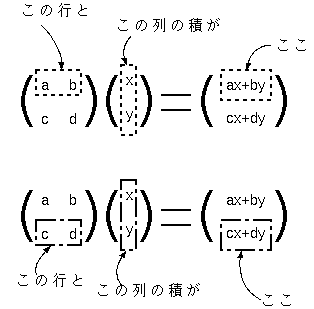
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
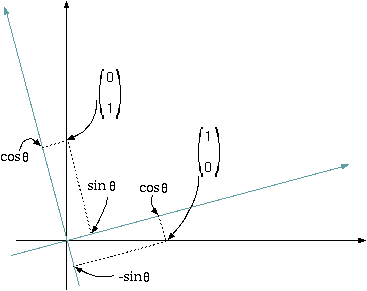 ˇˇ˛óĹľ¤Ç¤˘¤ë¤«¤éĹöÁł¤Ç¤˘¤ë¤¬ˇ˘¤ł¤ÎĽ°¤Ď
ˇˇ˛óĹľ¤Ç¤˘¤ë¤«¤éĹöÁł¤Ç¤˘¤ë¤¬ˇ˘¤ł¤ÎĽ°¤Ď
|
(2.15) |
|
(2.16) |
|
(2.17) |
|
(2.18) |
|
(2.19) |
|
(2.20) |
|
|
|
|
= |
|
|
|
|

| |
|
|
| |
|
|
|
(2.21) |
| |
|
|
| |
|
|
| |
|
|
|
|
(2.22) |