ここで
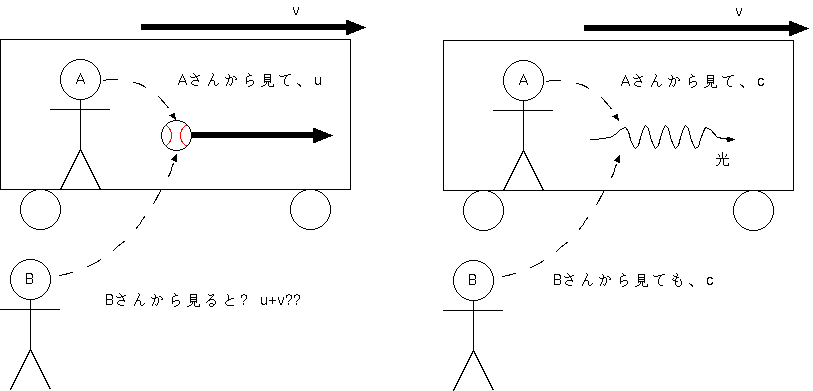
計算しようとしているのは、たとえば電車が速度vで走っているとし
て、電車の中で何か(たとえばボールとか、走り回る子供とか)が速度uで走ったとすると、果たして外から見るといくらの速度で進むように見えるか、という
問題。ガリレイ変換的常識ではもちろんu+vなのだが、相対論的常識は違う。そもそも電車内で動くものが光であった場合、電車の中でも速度c、外から見て
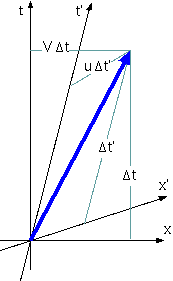
も速度cである。ということは、単純な速度の足算(V=u+v)は成立しないだろうと考えられる。では具体的に計算してみよう。

|
|
(6.3) |
|
(6.4) |
|
| V= | 0.5c+0.5c
|
=0.8c |
| V= | 0.5c+0.8c
|
= |
|
| V= | c+v
|
=c |
|
(6.5) |
|
(6.6) |
|
(6.7) |
|
(6.8) |

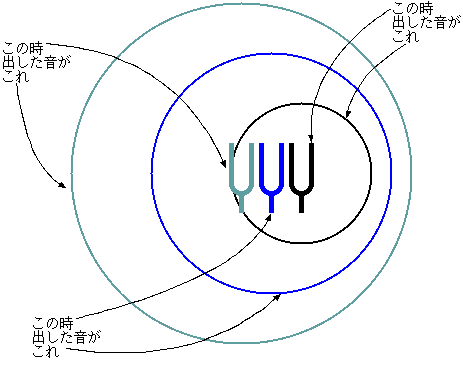 振動数fは波長λと音速Vによって、f=[V/λ]と書かれる。6.4.は、この式の分母の変化である。図で
書けば右のようになる。これは音源が動きながら音を出している様子である。音源が動いても、まわりの空気(音の媒質)はいっしょに動いているわけではない
ので、音を出した場所を中心として球状に(図では円状になっている)広がる。音が広がるまでの間に音源が移動しているので、前方では波がつまり(波長が短
くなり)、後方では波が広がる(波長が長くなる)。
これに対して6.4.は、f=[V/λ]の分子の方の変化である。同じ波長の波が来たとしても、自
分が波に立ち向かっていくならば、1秒間に遭遇する波の数が増える。逆に波から遠ざかるならば、波の数が減る。
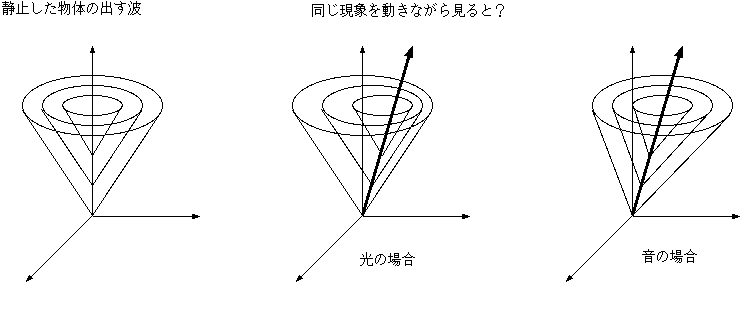
しかしこのような説明を聞いた後で、「さて光の場合のドップラー効果はどうなるのか」と考えると、ちょっと不思議なことに気づくだろう。音の場合、観測者
の運動によって音速が変る(6.4の場合)。だから音の振動数が変化するわけである。しかし光の場
合、そんなことは起きない(光速度不変の原理!)。では光の場合、「観測者が運動している場合のドップラー効果」は存在しないのか。もちろんそんなことは
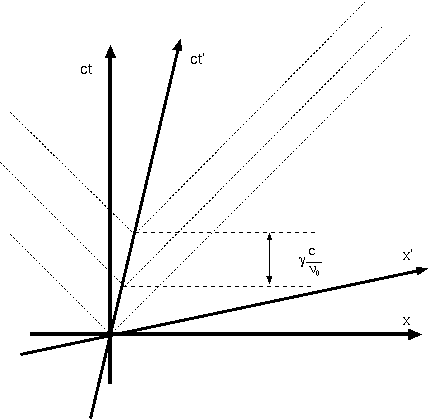
ない。以下で、まず図を書いて考えてみよう。
振動数fは波長λと音速Vによって、f=[V/λ]と書かれる。6.4.は、この式の分母の変化である。図で
書けば右のようになる。これは音源が動きながら音を出している様子である。音源が動いても、まわりの空気(音の媒質)はいっしょに動いているわけではない
ので、音を出した場所を中心として球状に(図では円状になっている)広がる。音が広がるまでの間に音源が移動しているので、前方では波がつまり(波長が短
くなり)、後方では波が広がる(波長が長くなる)。
これに対して6.4.は、f=[V/λ]の分子の方の変化である。同じ波長の波が来たとしても、自
分が波に立ち向かっていくならば、1秒間に遭遇する波の数が増える。逆に波から遠ざかるならば、波の数が減る。
しかしこのような説明を聞いた後で、「さて光の場合のドップラー効果はどうなるのか」と考えると、ちょっと不思議なことに気づくだろう。音の場合、観測者
の運動によって音速が変る(6.4の場合)。だから音の振動数が変化するわけである。しかし光の場
合、そんなことは起きない(光速度不変の原理!)。では光の場合、「観測者が運動している場合のドップラー効果」は存在しないのか。もちろんそんなことは
ない。以下で、まず図を書いて考えてみよう。
|
(6.9) |
|
(6.10) |
|
(6.11) |
|
(6.12) |