|
(7.1) |
|
(7.2) |
|
(7.3) |

|
(7.4) |
|
(7.5) |
|
(7.6) |
| ( |
|
) |
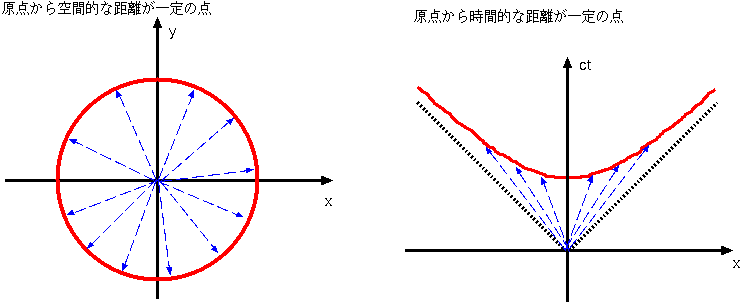
 4次元的な考え方と言っても内容は変わっていない。アインシュタイン自身もミンコフスキーがこういう書き方を始めた時、「数学的な話で、物理の理解とは関
係ない」と思っていたらしい36。し
かし、このような表示によって相対論を考えることが劇的に簡単になる(アインシュタインもすぐにそれに気づいて自分でも使い始めている)。
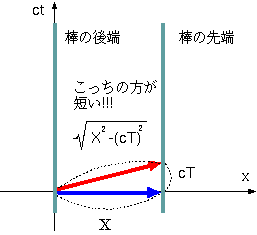
この「4次元的距離」という考え方をすると、ローレンツ短縮やウラシマ効果を別な形で理解することができる。ローレンツ短縮は、「動いている棒は長さが縮
む」という現象である。右の図は、棒が静止している座標系で、棒の先端と後端の軌跡を示した。図の水平矢印は、棒と同じ動きをしている人が観測する「棒の
長さ」である。
次に、棒に対して動いている人を考える。同時の相対性により、この観測者の同時刻は傾いている。この人が棒の長さを測る時には、自分にとっての同時刻を基
準に測るであろうから、「棒の長さ」は図の斜め矢印であると認識する。
水平矢印と斜め矢印は、グラフ上の見た目では斜めの方が長く見えるが、4次元的長さの自乗の定義がx2+y2+z2−(ct)2で
あることを思い出すと、水平矢印の長さXに対し、斜め矢印は長さが√[(X2−(ct)2)]となる(普通
のピタゴラスの定理とは(ct)2の前の符号が変わっていることに注意)。
ウラシマ効果は、動いている方が経過する時間が短いという効果であるが、それは図の斜め線の方が垂直な線より短いということで理解できる。
4次元的な考え方と言っても内容は変わっていない。アインシュタイン自身もミンコフスキーがこういう書き方を始めた時、「数学的な話で、物理の理解とは関
係ない」と思っていたらしい36。し
かし、このような表示によって相対論を考えることが劇的に簡単になる(アインシュタインもすぐにそれに気づいて自分でも使い始めている)。
この「4次元的距離」という考え方をすると、ローレンツ短縮やウラシマ効果を別な形で理解することができる。ローレンツ短縮は、「動いている棒は長さが縮
む」という現象である。右の図は、棒が静止している座標系で、棒の先端と後端の軌跡を示した。図の水平矢印は、棒と同じ動きをしている人が観測する「棒の
長さ」である。
次に、棒に対して動いている人を考える。同時の相対性により、この観測者の同時刻は傾いている。この人が棒の長さを測る時には、自分にとっての同時刻を基
準に測るであろうから、「棒の長さ」は図の斜め矢印であると認識する。
水平矢印と斜め矢印は、グラフ上の見た目では斜めの方が長く見えるが、4次元的長さの自乗の定義がx2+y2+z2−(ct)2で
あることを思い出すと、水平矢印の長さXに対し、斜め矢印は長さが√[(X2−(ct)2)]となる(普通
のピタゴラスの定理とは(ct)2の前の符号が変わっていることに注意)。
ウラシマ効果は、動いている方が経過する時間が短いという効果であるが、それは図の斜め線の方が垂直な線より短いということで理解できる。
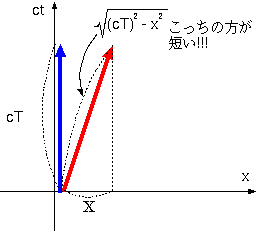 グラフを見ると斜め線の方が長く見える
が、今長さの定義が4次元的距離で定義されていることに気をつけなくてはいけない。そのため、真っ直ぐな線の4次元的距離の自乗は−(cT)2で
あり、斜め線の4次元的距離の自乗は−(cT)2+X2
となる。「距離の自乗」がマイナスになるのは「自乗」という言葉の本来の意味からすると奇妙であるが、今「距離の自乗」は−(cT)2+x2+y2+z2と
定義されているのでこれでよい。本来の意味とは違う使い方をしていることになるが、物理専用の用語なのだと思って納得して欲しい。
マイナスになるのが気になるのであれば、「時間的な距離を測る時には距離の自乗は(cT)2−x2−y2−z2と
定義する」と決めておいてもよい。
グラフを見ると斜め線の方が長く見える
が、今長さの定義が4次元的距離で定義されていることに気をつけなくてはいけない。そのため、真っ直ぐな線の4次元的距離の自乗は−(cT)2で
あり、斜め線の4次元的距離の自乗は−(cT)2+X2
となる。「距離の自乗」がマイナスになるのは「自乗」という言葉の本来の意味からすると奇妙であるが、今「距離の自乗」は−(cT)2+x2+y2+z2と
定義されているのでこれでよい。本来の意味とは違う使い方をしていることになるが、物理専用の用語なのだと思って納得して欲しい。
マイナスになるのが気になるのであれば、「時間的な距離を測る時には距離の自乗は(cT)2−x2−y2−z2と
定義する」と決めておいてもよい。
|
(7.7) |
|
(7.8) |
|
(7.9) |
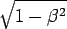 倍である。
固有時は、各物体ごとに違う進み方をする。上の式からわかるように、寄り道をするとdx2が多くなり、結果として固有時の進みは
遅れる(ウラシマ効果)。双子のパラドックスの計算なども、運動している物体の固有時が短くなる、と考えれば簡単である。
我々の知っている粒子の世界線はtime-likeであるかnull-likeであるか、どちらかである。世界線がspace-likeだということは
超光速で運動している粒子であるということで、そんなものは見つかっていない。もし見つかったら、そのような粒子は見る人の立場によっては未来から過去に
向かって走ることになるので、因果律に抵触することになるだろう。
世界線がnull-likeになると、固有時の変化dτは0になってしまう。よって光のように光速で動くものに対しては固有時が定義できない(あるいは
定義してもそれは変化しない)。
倍である。
固有時は、各物体ごとに違う進み方をする。上の式からわかるように、寄り道をするとdx2が多くなり、結果として固有時の進みは
遅れる(ウラシマ効果)。双子のパラドックスの計算なども、運動している物体の固有時が短くなる、と考えれば簡単である。
我々の知っている粒子の世界線はtime-likeであるかnull-likeであるか、どちらかである。世界線がspace-likeだということは
超光速で運動している粒子であるということで、そんなものは見つかっていない。もし見つかったら、そのような粒子は見る人の立場によっては未来から過去に
向かって走ることになるので、因果律に抵触することになるだろう。
世界線がnull-likeになると、固有時の変化dτは0になってしまう。よって光のように光速で動くものに対しては固有時が定義できない(あるいは
定義してもそれは変化しない)。
|