青字は受講者からの声、赤字は前野よりの返答です。
タブレットを使っての授業は初めてだった。高校の時までは微分、積分は計算ばかりで意味をよく考えてなかったけど、これからの授業で学んでいきたいと思う。
意味がわからないと「使える数学」になりません。頑張りましょう。
タブレットでの授業を始めて受けました。とても分かりやすかったのですが、どうしても${\mathrm dy\over\mathrm dx}=y$のグラフのイメージがつきません。もう一度、自己学習してみたいと思います。
じっくり考えてみてください。質問あったらいつでもどうぞ。
今後数学をしっかり学びたいと思った。また様々な式を図にしてみると面白いと思いました。
しっかりやっていきましょう。図で考える癖はつけましょう。
タブレットを使った授業はおもしろかった。アニメーションもわかりやすくて、イメージしやすかった。
これからも使っていきます。
タブレット・プリントと２つとも図を使った授業だったのでとてもわかりやすかった。
図解は大事です。イメージをつけながら数学しましょう。
微分（＝傾き）を図で見ることで、わかりやすく理解した。
先生は質問されるのが大好き。
はい、どんどん質問してください。
物理をするためには数学が大切だということを知ったので授業をしっかり受けてしっかり復習していこうと思いました。
はい。復習して手を動かして、数学を身につけてください。
今日は、高校の内容の他に${\mathrm dy\over\mathrm dx}={y\over x}$という関数のことについて知れたのでよかった。もっといろんなことを知っていきたいと思う。
いろいろと新しいことを勉強していきましょう！
微分の意味は今までまったくわからなかったけど、今日少しだけわかった。
これからの授業でもじっくりやるので「少しだけ」でなく完璧にしていってください。
授業は集中して全部聞き逃さないように頑張ります。タブレットを使った授業がはじめてでわくわくしました！！
集中よろしく。わくわくを持続させていきましょう。
いろんな方程式の図を見れてよかった。なんでこんな図になるのかと興味が湧いた。
これから先の授業で少しずつ、種明かししていきます。
微分方程式とは簡単に言えばどういうものなのかが分かりました。
後でもっと深く、微分方程式とつきあいましょう。
高１のときのオープンキャンパスで「タイムマシン」についての面白い話を聞いたのですが（理学部のイベントで）あの話をされたのは前野先生でしたでしょうか？
はい、それはまず間違いなく私です。
数学のとらえ方が少し変わった。授業もタブレットを使ってとても分かりやすかった。
自然科学の勉強に役立つ道具として、数学もタブレットも活用していきましょう。
前野先生！！イントロすごく良くて感動しました！今日はやる気に満ちて過ごせそうです！ちなみに、この授業で習う以外の数学を先生に聞いても良いのでしょうか？
それはどうもありがとう。やる気出して頑張ってください。質問はもちろん、答えられることならなんでもいいです（答えられないときはごめん）。
難しい授業になりそうだと思ったけど、頑張ってついていきたいです。
難しいけど、わかれば面白いので、頑張ってください。
ニュートンについて知らなかったことがわかったので良かった。自分が見たことのない関数がたくさんあるのだと分かった。
これからも「知らないこと」がたくさんでてきます。自分のものにしていきましょう。
${\mathrm dy\over \mathrm dx}={ay\over x},{ax\over y}$など、式の中に$y$が入っている数式は元の形に直すとどんな式になるのでしょうか？
「元の形」？？？？ 元も何も、$y$は$y$ですが。
質問したかったことしてくれたので、スッキリしました。図形をイメージすることの大切さを今日は学びました。来週の授業ではたくさん質問したいと思います。
では、次回はあなたが質問して、みんなをスッキリさせましょう。
高校での微積はこういうときはこうみたいな感じであまり好きじゃなかったけど、今日は図とかでぐにゃぐにゃなったりして面白かったです。
微積でもなんでも、数学って本来は面白いもんですよ。
タブレットを使う授業は始めてで、楽しかった。また授業がわかりやすそうで安心しました。これからの授業が楽しみになりました。
これからも、お楽しみに。
${\mathrm dy\over \mathrm dx}=x$などのグラフを見ると２次曲線になるのを見て感動した。
グラフと式を頭の中で結びつけていきましょう。そうすれば数式にも感動がある。
高校までは主に数式や文字で説明を受けたので、タブレットを使ったビジュアル的な方程式はわかりやすくてとてもよかった。
頭にイメージを植え付けましょう。
私は図の方がわかりやすいので、タブレットをつかって図などが見れるのはありがたいです。
イメージを豊かに持っていきましょう。
自然科学を万人が理解できるようにするための道具が数学である。
その通りです。この授業でその道具を手にいれてください。
高校で習ったことを忘れていたので、復習できてよかったです。
なんか心配になるコメントだなぁ。習ったことは頭と身体に染みつけて、忘れないようにしないと。
もともと数学は好きなので楽しかった。自然科学を数学てで解いていくのはどっちも好きなので楽しみです。集中してがんばっていきたい。
集中して、楽しんでください。
自分もよく高校の頃は自転車で問題を解いていたので、今日の話はよくわかりました。今日の授業でわからない事はなかったのでまた次回質問します。よろしくお願いします。
どんな時でも（自転車乗ってても）学問はできる。質問はこちらこそ、よろしく。
数学が少し好きになりそう。イメージすると分かりやすいことがよく分かった。
イメージ豊かに、好きになってください。
今まで数式で全てをとらえていたのを視覚的にとらえられて理解がより深まりました。
数学はいろんな方向から攻めていきましょう。
グラフの線が予想したのとちょっとずつ違っていてあれ？と思いもしましたが、式だけで出されるよりは図で見た方がわかりやすかったです。
予想がズバズバと当たるようになりましょう。
宜しくお願いします。
こちらこそ宜しく。
タブレットを使ってグラフで見ることでとてもわかりやすかったです。
イメージを大切にしていきましょう。
集中する、前を向く。
トイレは自由。
mathは味方。
理解→式→式分野
→図→図分野
授業は復習で自己学習
∈ってなんでしたっけ？
それぞれ今日話した注意事項ですね。∈ってのは「集合に含まれる」の記号かな？？
今日は特にわからないところはありませんでしたが、微分積分にはかなり苦しめられた過去があるので、今後のことを考えると、不安を感じます。
わからなくなったら質問をよろしく。
大学受験の数学と大学で学ぶ数学は全然違うことを実感した。
中身は同じ（もちろん難しくはなるけど）なんですが、取り組む姿勢は変わってくる（変わらないと困る）かもしれませんね。
自分は高校の時の物理の授業がわかりづらく、いつも一人でやったり友達とやったりしておりました。これから授業は楽しくできるよう、しっかり理解できるようにしていきたい。
質問ありましたらいつでもどうぞ。また仲間同士でも教え合いましょう。
高校でやったことを改めて、理解できたり、理解できなかったことを理解できそうでした。やっていて思いました。
理解をどんどん深めていきましょう。
高校よりも難しい曲線がいくつもあっておどろいた。
まぁ、大学来たんだから高校より難しいことをどんどん学ばないとね。
タブレット端末は使ったことがなくて少しとまどいましたが新鮮でよかったです。
今後、どんどん使っていくことになります。
私は数学が得意ではないので、頑張って勉強して、より理科の理解を深められるようにしたいです。よろしくお願いします。
科学をやるには数学を得意にした方が絶対いいです。頑張りましょう。
高校でなんとなく計算できるようになってた微積は、実は自然化学を解明するために発明されたなど、微積の実用性について聞いてびっくりした。おもしろかった。タブレットの図は興味を持てた。もっと遊んでみたい。
これからも使いますし、最初のページに書いたようにダウンロードもできます。
微分は公式どおりというか、傾きを求めるためと聞いていたけど、もっと深いところがわかった。あと、ニュートンはすごいと思う。
勉強していくと、深いところもニュートンのすごさもどんどんわかってくると思います。
初めてタブレットを使った授業をしたのでおもしろかったし、視覚的に考えられてよかった。
アニメーションで得たイメージを大事にして勉強していきましょう。
「微分したら傾きがわかる」という意味が図解でよく理解できました。すごく興味の湧く講義でした！
興味を持続させていきましょう！
すごいおもしろい先生だと思いました。$-{x\over y}$の線がおもしろいなぁと思いました。これからも数学を楽しんでいきたいです。
おもしろく楽しく数学しましょう。
物理とかを学ぶためには数学も必要とはあまり知らなかった。タブレットを使いながらの授業は初めてだったのでとてもおもしろかった。
いやいや、数学は重要ですよ。がんばっていきましょう。
授業の進め方がわかった。
微分のことがアニメーションで振り返れたのでよかった。
入試以来勉強してなかったので、これから頑張って行きたい。
これから先は勉強にどっぷり浸かってください。
微分方程式の意味というか根本的なことを理解することができ、高校のときなぜこういうことをやっていたのかを知ることができました。初めてタブレットを使った授業でとても楽しかったです。
何を何のためにやるのかがわからないと、面白くないですよね。面白く楽しい数学をしましょう。
初めてタブレット使った。テンション上がる。
図のアニメがあるのでとてもわかりやすい。最終的に数式を見るだけで図がイメージできるようになりたい。
これからもテンション上げていきましょう。イメージあふれる数学を。
色々なグラフを見て少し微積が楽しそうだなと思いました。
楽しく勉強しましょう！
タブレット端末を使用した授業を初めて受けたが、図もわかりやすかった。
これからもどんどん使っていく予定です。
数学は昔からあまり好きではなかったけど、微分の意味やアニメーションを使った授業はとても興味があります。これからがんばります。
興味を持続させて、数学好きになってください。
先生の授業が塾の楽しく覚えられるような授業みたいで自分もこういう授業が好きなのでこれから楽しみです。
楽しく数学やっていきましょう。
ハイテクすぎておどろきました（笑）。数学苦手だけど授業楽しいのでがんばれそうです！！
これからよろしくお願いします\(^^)／
最後には数学得意になってください。こちらこそよろしく。
という記号で表現する）。
という交通標識は、道の傾きが0.1であることを示している。
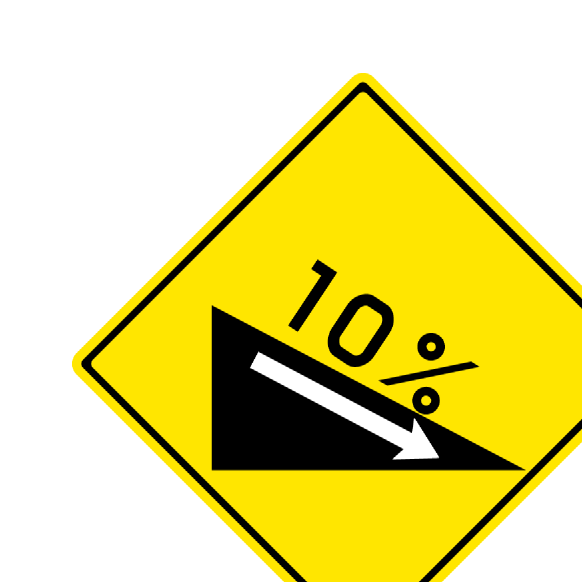は傾きが$-0.1$であることを示している（道路標識では上りか下りかは絵で表現され、数値としてはどちらでも10％と表現するが、数学における傾きでは下るときは傾きを負の数値とする）。