テイラー展開の例として、${1\over 1-{x}}$という関数のテイラー展開を考えよう。なぜこれを考えるかというと、この関数の「ある条件の元での展開」は微分を使わなくても出せる(よって、後で微分を使って出した展開式と比較できる)。
というのは初項1、公比${x}$の等比数列の和に関して
\begin{equation} {1-{x}^{N}\over 1-{x}}= 1+{x}+{x}^2+{x}^3+{x}^4+{x}^5+\cdots+{x}^{N-1}=\sum_{n=0}^N {x}^n\label{touhix} \end{equation}という公式があるこの公式を確認したければ、$( 1+{x}+{x}^2+{x}^3+\cdots)(1-{x})$を計算してみればよい。$1-{x}^{N}$になるはずだ。。$|{x}|<1$であれば、$\lim_{N\to\infty}{x}^N=0$になるから、
\begin{equation} {1\over 1-{x}}= 1+{x}+{x}^2+{x}^3+{x}^4+{x}^5+\cdots=\sum_{n=0}^\infty {x}^n\label{oneminux} \end{equation}と書くことができる。
これは確かにテイラー展開の式の形になっている。というのは、
\begin{equation} {\mathrm d \over \mathrm dx}\left({1\over 1-{x}}\right)={1\over (1-{x})^2},~~~ {\mathrm d \over \mathrm dx}\left({1\over (1-{x})^2}\right)={2\over (1-{x})^3},~~~ {\mathrm d \over \mathrm dx}\left({2\over (1-{x})^2}\right)={2\times 3\over (1-{x})^4},\cdots \end{equation}のように順に計算していくと
\begin{equation} \left({\mathrm d \over \mathrm dx}\right)^n \left({1\over 1-{x}} \right)= n! \left({1\over 1-{x}}\right)^{n+1} \end{equation}であることがわかり、この式に${x}=0$を代入すると答えは$n!$となり、テイラー展開の公式に入れれば確かに${1\over 1-{x}}=\sum_{n=0}^\infty {x}^n$という式がちゃんと成立するからである。ところが、上で$N\to\infty$の極限を取ったときに${x}^N\to0$となるのは(級数の和を${1\over 1-{x}}$にできるのは)$|{x}|<1$の時だけである。つまりこの式が成立するのは、$-1<{x}<1$という範囲だけなのである。

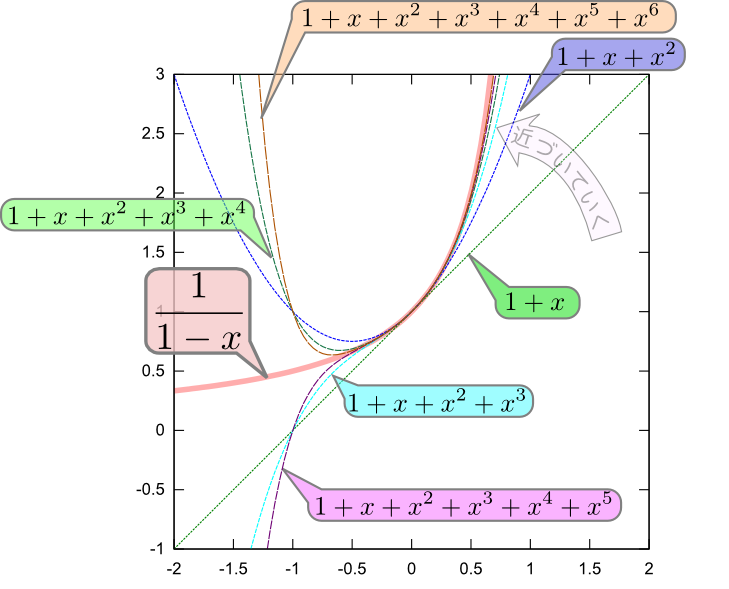
上のグラフは$1,1+{x},1+{x}+{x}^2,\cdots$と展開を一個ずつ取っていったときに、グラフがどのように${1\over 1-{x}}$に近づいていくかを示したものだ。これを見ると確かに$-1<{x}<1$の範囲で見ると項が増えるごとに${1\over 1-{x}}$のグラフに近づいていくように見える。
しかし、この「近づいていく」という計算は、$-1<{x}<1$の範囲から離れてしまうともはや正しくない。
${x}=1$が「ここを超えるとテイラー展開できない点」になるのは考えてみればあたりまえで、そもそもテイラー展開の式は一階微分から初めて$n$階微分による影響を計算していくことで関数の値を求めようというものであるが、${x}=1$のところで関数$f({x})={1\over 1-{x}}$は定義されておらず不連続で微分もできないから、「微分を使って値を求める」という計算であるテイラー展開が破綻するのは当たり前である「公式や定理は「適用限界」を超えて使ってはならない」を教訓として刻んでおこう。運良くそれでも大丈夫な場合もあるかもしれないが、確認は必要である。。実際、${x}>1$の範囲では${1\over 1-{x}}$は負にならなくてはいけないが、$1+{x}+{x}^2+{x}^3+{x}^4+{x}^5+\cdots$は正にしかなりえず、もちろん負の値を採っている${1\over 1-{x}}$に近づくことはない。
一方、${x}=-1$のところを見ると、$1,1+{x},1+{x}+{x}^2,\cdots$は$1$と$0$を振動している。これは式の上でも明らかで、$1+{x}+{x}^2+{x}^3+{x}^4+{x}^5+\cdots$という式は${x}=-1$の時は
\begin{equation} \underbrace{\underbrace{1-1+1-1+1-1}_{ここまでの和は0}+1}_{ここまでの和は1}-1+1-1+1+\cdots \end{equation}のような式になるので、奇数個の項があると答は1、偶数個の項があると答は0である。一方、大本の${1\over 1-{x}}$は${x}=-1$ではその中間である${1\over 2}$になるこれは「$1-1+1-1+1-1+1-1+1-1+1+\cdots={1\over 2}$だ」と主張しているのではない。むしろ「こんなふうに無限和を計算してはダメだ」と主張している。後で説明する収束半径を考慮しない計算だからである。。
この展開式を、
\begin{equation} {1\over 1-{x}}=1+{x}+{x}^2+\cdots + {x}^{N-1} + \underbrace{{{x}^{N}\over 1-{x}}}_{剰余項} \end{equation}と表すこともできる。「剰余項」と示した部分は、${1\over 1-{x}}-{1-{x}^{N}\over 1-{x}}$という計算の結果である。剰余項の部分が$N\to\infty$で消えてしまうような状況になっていないと、テイラー展開は正しい展開にはなっていないということになる。
このように、テイラー展開のように多項式で展開する時は、「どの範囲までが展開可能なのか」をちゃんと判断しないと間違えた展開の仕方をしてしまうことになる。
同じ式${1\over 1-{x}}$を、${x}=0$ではなく${x}=2$の周りで展開すると(↑のグラフでやってみてもよい)、
\begin{equation} {1\over 1-{x}}=\sum_{n=0}^\infty {1\over n!}\left(\!{\mathrm d \over \mathrm dx}\!\right)^n \left({1\over 1-{x}}\right)\biggr|_{{x}=2} ({x}-2)^n \end{equation}となる。
\begin{equation} \left(\!{\mathrm d \over \mathrm dx}\!\right)^n\!\! \left({1\over 1-{x}}\right) =n!\times {-1\over (1-{x})^{n+1}} \end{equation}なので、これはつまり、
\begin{equation} {1\over 1-{x}}=\sum_{n=0}^\infty (-1)^{n+1} ({x}-2)^n\label{sumxn} \end{equation}ということである。$n$の上限を少しずつ大きくしていくと、
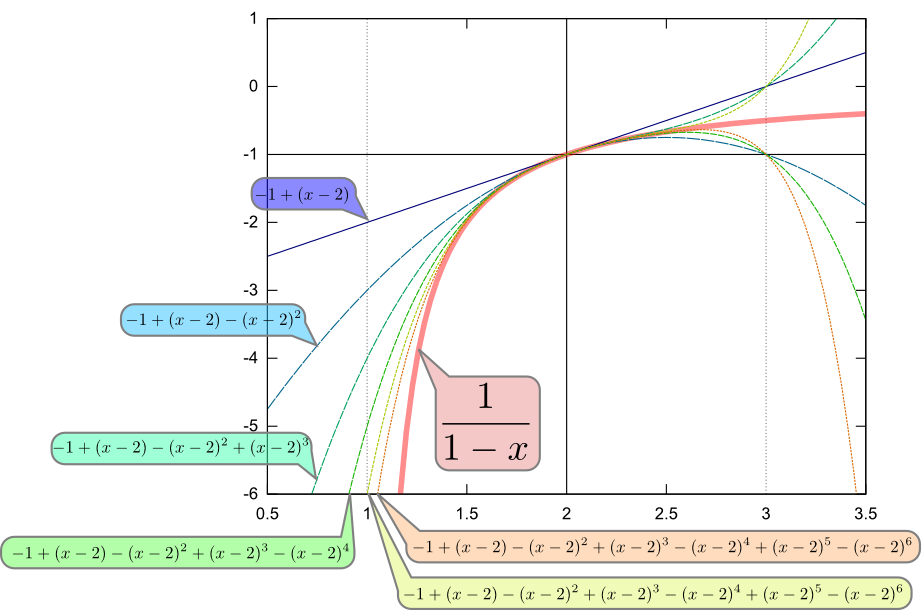
というグラフに示したように線は${1\over 1-{x}}$に近づいていく。ただし、「近づいていく」と言えるのは$1<{x}<3$という範囲(つまり$|{x}-2|<1$の範囲)だけである(${x}\geq 3$では激しく振動してしまうし、${x}<1$では全く近づかない)。このように、テイラー展開には有効な範囲がある。テイラー展開の中心から「テイラー展開できなくなる値」までの距離を「収束半径」と呼ぶここでは${x}$という一次元量を扱っているので「半径」というのは変なのだが、そういう呼び方をすることになっている。。
冪級数が$\sum_{n=0}^\infty a_n ({x}-x_0)^n$という形で書かれている時、
\begin{equation} \lim_{n\to\infty}{1\over \sqrt[n]{|a_n|}},~~\lim_{n\to\infty}\left|{a_n\over a_{n+1}}\right|\label{shusokuhankei} \end{equation}のどちらかが存在していれば、それが収束半径になる、ということがわかっている。今の場合、$|a_n|=1$だから収束半径は確かに1である。
←11講の最初へ 指数関数のテイラー展開へ→