今日の問題

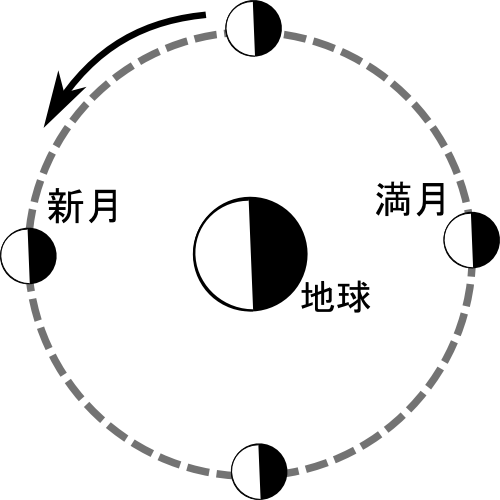
地球から火星を見た図(←)を参考に、地球から金星を見るとどのように見えるかを図解してください。
ヒントとして、地球と金星では金星の方が速く回ってます。
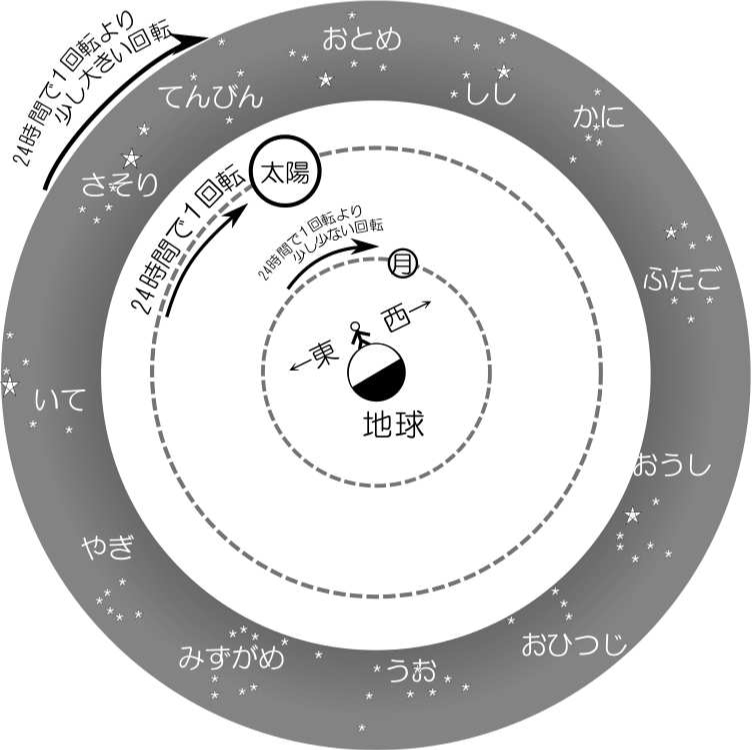
↓の状態までは黒板に絵が書いてありました。
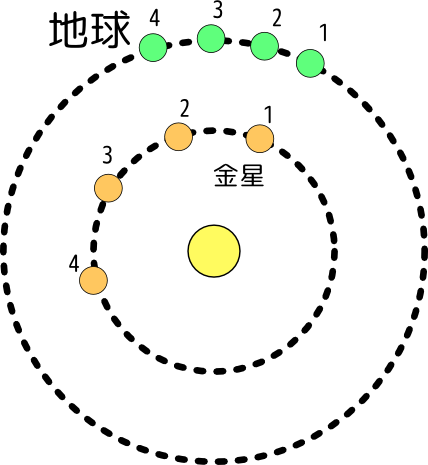
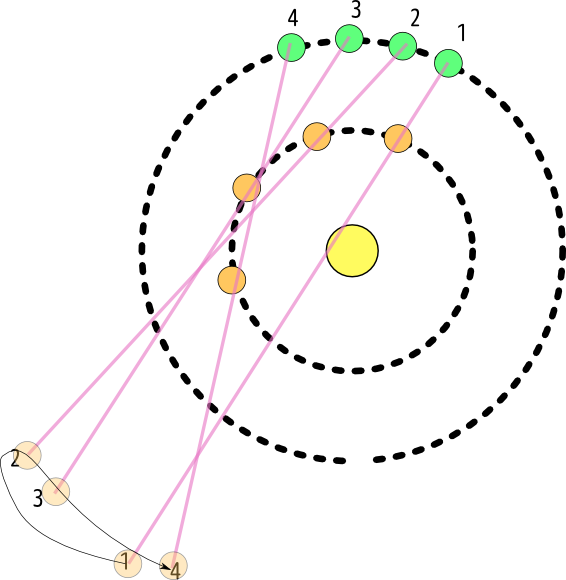
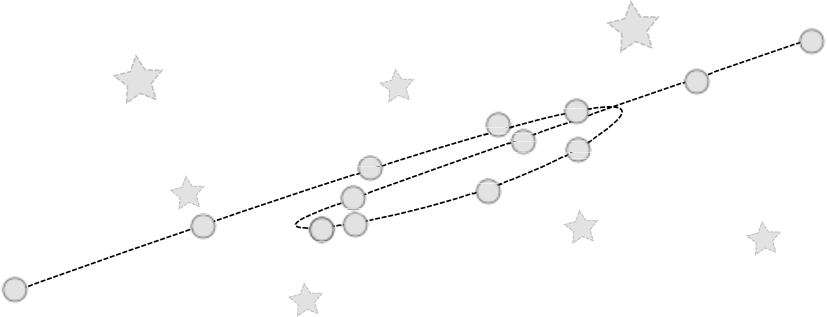
正解は左の通りです。地球から金星を見たらどんなふうにみえるか、なので、地球→金星と結ぶ線(いわば視線)を伸ばして、「地球から見ると金星がどっちに見えるか」を表現して欲しかったわけです。
図をさらにどんどん書き進めてくれた人もいて、そういう人は金星が「いったりきたり」する様子がわかったのではないかと思います。
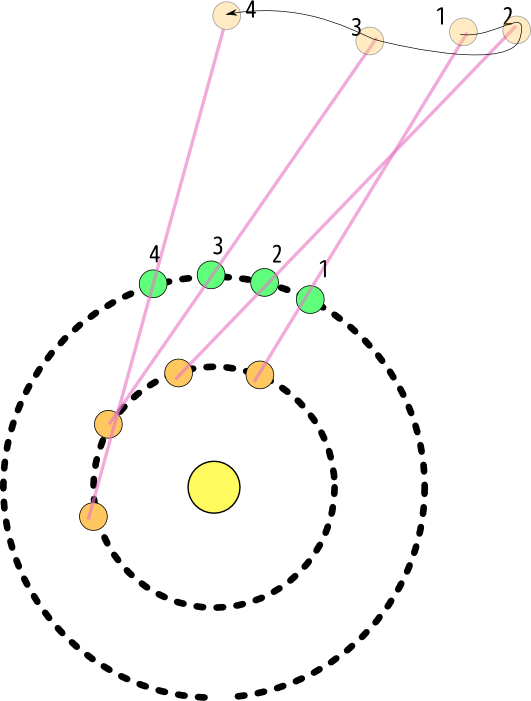
右の図が一番多かった間違い。これだと金星→地球という線になってますから、「金星から見ると地球がどう見えるか」という図になってしまっています。金星人の気持ちになってしまいました。
この他にも、
・なぜか地球が中心にいて金星が周りを回ってしまっている図
・地球から金星まで線を引っ張っているが、そこで止まってしまっている図(これでは、「どっちに見えるか」が示せてない)。
・なぜか地球が動いてない図??
などなどの変な解答がありました。わざと細かい図の書き方などを説明せずに出した問題なので、かなり変なのもありましたが甘〜〜〜〜〜〜く採点してます。
感想・コメントなど
青字は受講者からの声、赤字は前野よりの返答です。
虹も太陽の7色の光によって出来たものですか?
そうです。水中にある水滴(雲とか雨とか)に光が入って屈折しつつ反射する時に角度が色によって違うために色がつきます。
日本の空よりアメリカの空の方が青色が薄く見えたのも、太陽との距離が違うからなのかな、と思いました。
日本の空でも、空気の状態によって違ったりもするので、なかなか単純ではないです。沖縄の空は綺麗です。
惑星の動画の動きが面白かった。よくこんなのから実際の運動がわかるなと思った。
確かに、これ結果を知ってなくて予想するのは難しいですよねぇ。
ブラックホールを人工的に作ることは可能ですか?
現代の技術で、ということなら無理です。超未来の「太陽のような天体をほいほい動かすほどの技術」があればできます。
なぜ学者は宇宙のことを知る必要があるのかと思った。
「知りたいから」という以外には必要性はないんじゃないかと思います。知ったことで何か役に立つことがあるかもしれないし、ないかもしれない。でも「知りたい」という気持ちは大事です。「役に立つ」は後からついてくる。
宇宙の端っこを観測することはできないのではないだろうか。
宇宙が膨張しているために、「ここから向こうは観測できない」という地平線のようなものはできます。そういう話もこの授業でいつかできるかな。
トンカチで太陽中心を実感できるのは驚きだった。
物理現象を見る力があれば、宇宙のこともわかるようになる、という例です。
惑星は互いにぶつかったりしないのかな?
今日の図で見たように、軌道が重なっていないので大丈夫です。小惑星だとか彗星だとかは惑星にぶつかったりすることもあります。
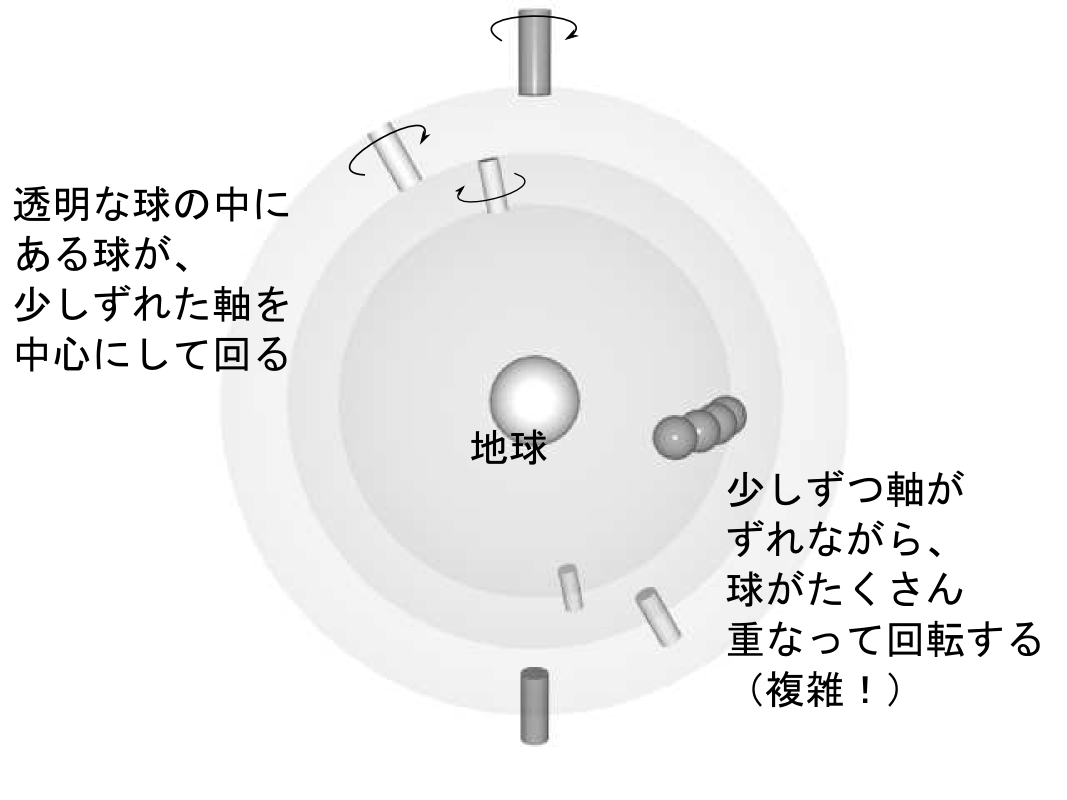
惑星の軌道はずれたりしないで、ずっとこのままですか?
だいたい、そのままです。これも万有引力の法則からくるんですが。しかし何百万年の間には少しずつ変化します(たとえば月は1年に数センチという割合で少しずつ遠くなっている)。
当時の常識が覆されたように、現代にも桃園のようで実は間違っているということがあるのかなと感じました。
あるかもしれません。ただ大事なことは、常識を覆すにはそれだけの証拠の積み上げが必要になる、ということです(天動説→地動説にしても、長い努力があってやっと認められた)。だからこれから常識が覆されることがあったとしても、それは「地道な努力の結果」として得られるものだろうと思います。
だいぶ前に相対性理論が間違っていた(光より速い物質が見つかった)というニュースがありましたが、続報を効いてません。
結論を先に言うと、あれは実験のミスでした(それは報道されたんですが、訂正ニュースってたいてい、最初のニュースより扱いが小さくなるんですよ)。それが「相対性理論が間違っていた」というニュースになってしまったのは、いろいろ問題があって、もともとその実験結果を論文にした人達も「おかしなデータが出ていて、これが本当だったら相対論間違えてることになっちゃうかもしれないからみんなで理由考えて」というふうに発表したのに、それが報道だと「相対論間違ってた!」「超光速だ!」になっちゃうんですね(やっぱり大げさに言った方がニュース見てもらえるからか)。あと、一つの実験データが出たからといって、即座に「相対論間違っていた」ということには、普通なりません。上にも書きましたが、常識を覆すには「地道な努力」の積み上げが必要です。
地球が住めない環境になった時、地球以外の惑星に人が移住するというのは有り得る話ですか?
太陽系内だと、普通に人が住める場所は(地球以外には)ありません。太陽系の外だと、遠すぎてなかなかいけません(行けるようになれば、地球みたいな星を探せるでしょう)。地球を大事にするしかないようです。
問題が難しすぎるので優しくして欲しいです。
その分、採点を甘くしてます。
惑星以外の星は動いてないのですか。
いえ、もちろん動いてます。
太陽もどこかを回ってますか。
太陽は他の恒星と一緒に「銀河系」という星の集まりを作ってますが、その銀河が回転してます。つまり太陽も銀河中心の周りを回っています。
教卓を横にずらしてもらえるとプロジェクタが見やすいです。
はい。
太陽が沈まない国があるという話を聞きましたが、どういう原理で沈まないのですか。
地球の自転軸が傾いているからです。

惑星は全部同じ方向に回っているのですか。
公転はそうです(物質がそういう方向に回っている状態から惑星ができていったのでしょう)。自転は逆回り(金星)や横倒し(天王星)があります。
地球と太陽の距離はどれくらいですか。
1億5千万キロ程度です。
STAP細胞の件ですが、論文云々よりもSTAP細胞自体に興味がある。もう一度実験してSTAP細胞自体が存在するのか確かめて欲しいと思います。
論文というのは「STAP細胞存在の証拠を示す」ためのものです。それに不備があって、今はあると思っていた「証拠」がなくなってしまった、という状況です。あるかどうかを示すには、ちゃんと証拠が出せる実験を積み上げていくしかないわけです(それが科学というもの)。
夜空に結構早めのスピードで動いている光があったんですが、人工衛星って地球から見えますか?


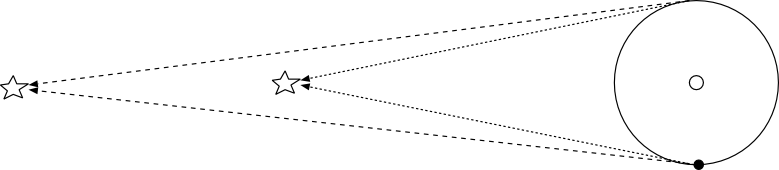


 右の図が一番多かった間違い。これだと金星→地球という線になってますから、「金星から見ると地球がどう見えるか」という図になってしまっています。金星人の気持ちになってしまいました。
右の図が一番多かった間違い。これだと金星→地球という線になってますから、「金星から見ると地球がどう見えるか」という図になってしまっています。金星人の気持ちになってしまいました。
