第3講 静止しているのは誰?
前回は「地球が止まっているのか、それとも太陽が止まっているのか」という話をしました。そういうことを考えていくと「止まっているとはそもそもどういうことか」というところまで考えてなくてはいけなくなります。
素朴な疑問ほど答えにくいものはない
さて、まずひとつの「そぼくなぎもん」から始めましょう。
その、西原さんのエッセイの中に、次のような疑問を投げかけたものがあった。
実は私にはずーーっと不思議だったのだが、バカにされるかもしれないので人前では言えなかった疑問がある。こっそりきいて、何度教えてもらってもわからんのだ。思いきって言う。
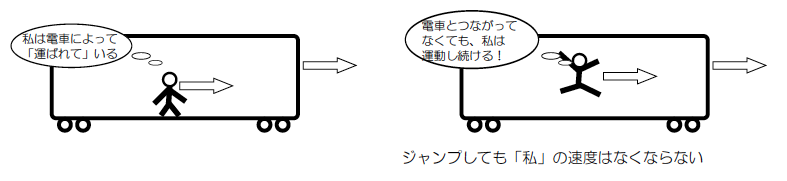
走っている電車の中で飛びあがった時、どうして飛び上がったその、同じ地点におりてくるのだ。変じゃないか。
―「おもしろくても理科」(清水義範著)より
西原さんの疑問にあなたは答えられるでしょうか?---引用した「おもしろくても理科」の中では、著者の清水義範氏が、この説明に悪戦苦闘しています。
さて、実際この疑問に納得いくように答えることは非常に難しいのですが、ではなぜ難しいのか、というところを考えてみましょう。なぜこんな話から始めたかというと、ここまでで話してきた「地球が動いているのか、太陽が動いているのか?」ということを考えるうえでとても重要な疑問だからです。
というのは、コペルニクスやガリレオなど、中世において地動説(太陽が止まっていて地球が動いている)を唱えた人が多く投げかけれられる疑問が
というものだったからです。この点我々現代人はガリレオよりも楽な状況にいます。だって「電車や飛行機に乗った時のことを考えてごらん」と言えるので(ガリレオは船で説明しています)。
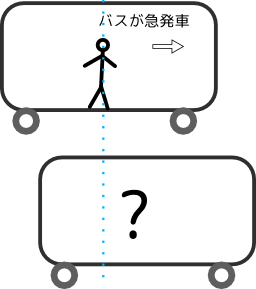
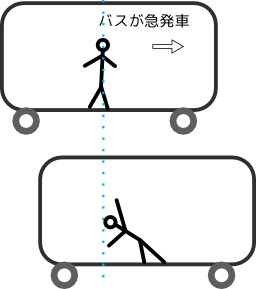
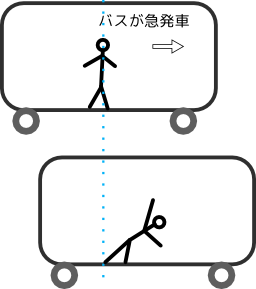
地球が動いているとすれば振り落とされるだろう、という考え方は、自分が乗っている物体(昔なら馬車とかなのでしょうか)が動き出した時に放り出されるイメージが残っているからでしょうか。「自分」は「この場所」に静止していて、地球だけが動いていってしまう、というイメージを持ってしまうからでしょう。
では、「動き出した馬車」から振り落とされることはあっても、「動いている地球」からは振り落とされないのはなぜでしょう??(違いがわかりますか?)
アリストテレス的考え---素朴な直感をそのまま法則化する
ここで重要になってくるのが、物体の運動に関してのアリストテレス的な考え方とニュートン的な考え方、その違いです。アリストテレスは「哲学者」と呼ばれます。「物理学者」とはあまり呼ばれません。しかし、アリストテレスの生きていた時代には、この二つの区別はないといっていいでしょう。「自然を考える」ことも「人間を考える」ことも、全部哲学者の仕事だったのです。
アリストテレスとニュートン、二つの考え方の、もっとも重要な違いは、アリストテレスが「運動するものは何であれ他のものによって運動させられる」と考えたことです。さらに「運動を引き起こすものは運動しているものと接触している」とも考えています。この考え方は実にもっともに聞こえます。それは我々の日常的経験からくる「ものは外から力を加えなければ動かない」という`直感'と一致しているからです。しかし、この実にもっともな'直感'が実は誤っているのです(そしてそれが、上の疑問につながってきます)。では、どこがおかしいのか。
アリストテレスの考え方の根底には何があったかというと、「目的論的秩序」という言葉で表されています。たとえば物体が落下するのは、物体の本来いるべき位置が地球の中心だから、そこを目的として運動するから、と説明します。そして目的地に到達すると、そこで静止すると考えていました。つまり「動く」ことには何か原因がなくてはいけないと考えたのです。
これを読んで「それでいいじゃないか」と思ったとしたら、あなたもアリストテレス同様、`直感'の罠に落ちていることになります。というのは、この「運動するには理由がいるはずだ」という`直感'が(おそらくは)次のようにつながることが、「電車でジャンプしたら後ろに降りるような気がする」という間違いに導くからです。
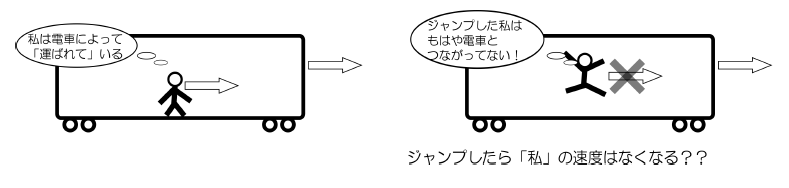
なんとなく「電車と足が接しているから人間は電車に運ばれている」と考えていませんか。これはある程度は(実は、電車が発車したり停車したりする時に関しては)正しいのですが、電車が等速で走っている時については正しくないのです。このアリストテレス的考え方の強みは、見た目からくる`常識'に即しているということです。これが改変されるまで、アリストテレスの時代である紀元前4世紀からガリレオが登場する17世紀まで待たなくてはいけなかったのも、この「`常識'を味方につけた」強みゆえでしょう。
もう一つのアリストテレスの自然観の特徴は、自然現象を天体などの「天上の世界」と地球表面の「地上の世界」に分け、別の法則に従っていると考えていることです。天体(月とか太陽とか)は誰にも押されることなく、地球の回りを回っているもちろん実際には太陽の回りを地球が回っている(地動説)んですが、アリストテレスは地動説ではなく天動説で考えています。のに対して、地球上では力を加えない限り運動は起きません(というのが`常識'です)。天上の世界は変化することなく同じ運動(円運動)を行い、地上の世界では物体はさまざまに動き回り、刻一刻と変化していく、という考え方をします。アリストテレスが天動説にこだわったのは、まさにこの天上と地上の分離という考え方に固執したからだ、と言っていいでしょう。ガリレオやニュートンは逆に「天も地上も同じ法則で動いている」ということを見つけていくことになります。
 のような矢印は力を表現しています。
のような矢印は力を表現しています。 のような矢印は速度です。速度の矢印の先から生えている
のような矢印は速度です。速度の矢印の先から生えている のような矢印は加速度です。
のような矢印は加速度です。