3次元極座標の単位ベクトル
3次元極座標をとる場合、$r$方向、$\theta$方向、$\phi$方向の単位ベクトルがrベクトルの方向により変わることをgifアニメで表現しています。
極座標を考えた場合の単位ベクトルはそれぞれ
\begin{align*} \bf{e}_{r} & = \sin\theta\cos\phi\bf{e}_{x} + \sin\theta\sin\phi\bf{e}_{y} + \cos\theta\bf{e}_{z}\\ \bf{e}_{\theta} & = \cos\theta\cos\phi\bf{e}_{x} + \cos\theta\sin\phi\bf{e}_{y} - \sin\theta\bf{e}_{z}\\ \bf{e}_{\phi} & = - \sin\phi\bf{e}_{x} + \cos\phi\bf{e}_{y} \end{align*}と書くことが出来るので、その時間微分は
\begin{align*} \dot{\bf{e}}_{r} & = \dot{\theta}\bf{e}_{\theta} + \dot{\phi}\sin \phi \bf{e}_{\phi}\\ \dot{\bf{e}}_{\theta} & = -\dot{\theta}\bf{e}_{r} + \dot{\phi}\cos \theta \bf{e}_{\phi}\\ \dot{\bf{e}}_{\phi} & = -\dot{\phi}\sin \theta \bf{e}_{r} - \dot{\phi}\cos \theta \bf{e}_{\theta} \end{align*}となります。
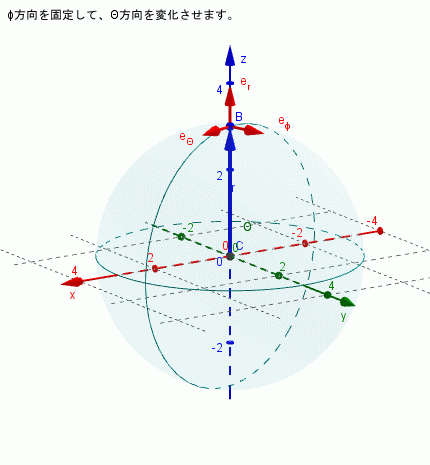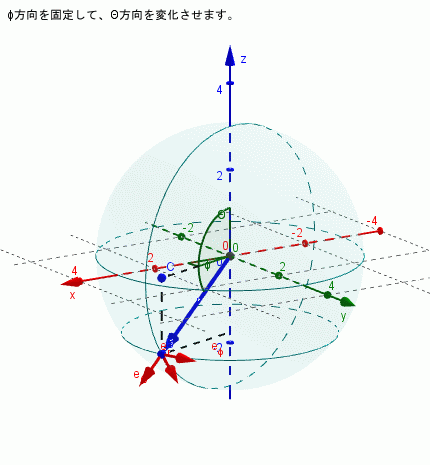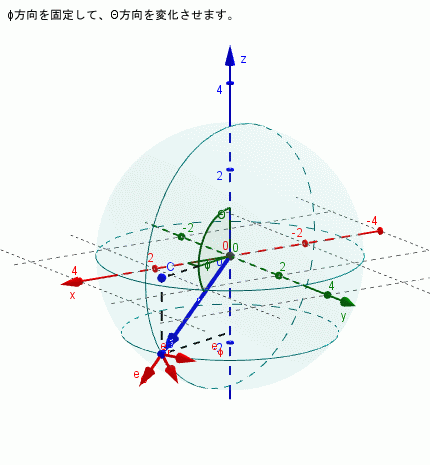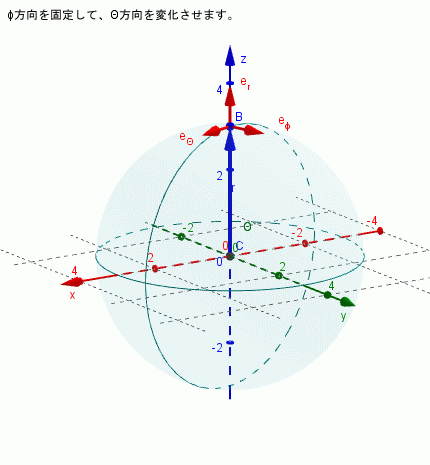
$\phi$を固定し($\dot{\phi}=0$)、θを変化させる場合
上式は
\begin{align*} \dot{\bf{e}}_{r} & = \dot{\theta}\bf{e}_{\theta}\\ \dot{\bf{e}}_{\theta} & = -\dot{\theta}\bf{e}_{r}\\ \dot{\bf{e}}_{\phi} & = 0 \end{align*}となり、e$\phi$は時間変化しない(向きは変わらない)ということになります。下図はそれを示しています。
$\theta$を固定し($\dot{\theta}=0$)、$\phi$を変化させる場合
上式は
\begin{align*} \dot{\bf{e}}_{r} & = \dot{\phi}\sin \phi \bf{e}_{\phi}\\ \dot{\bf{e}}_{\theta} & = \dot{\phi}\cos \theta \bf{e}_{\phi}\\ \dot{\bf{e}}_{\phi} & = -\dot{\phi}\sin \theta \bf{e}_{r} - \dot{\phi}\cos \theta \bf{e}_{\theta} \end{align*}となり、すべての単位ベクトルの向きが時間変化することがわかります)。下図はそれを示しています。
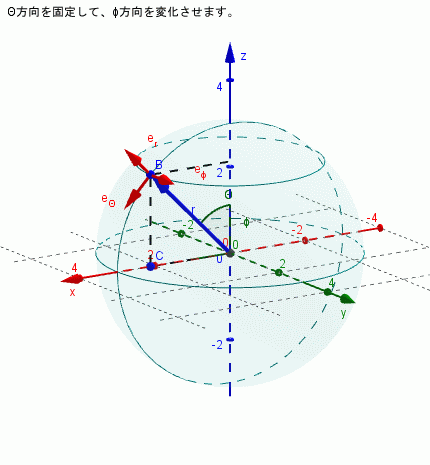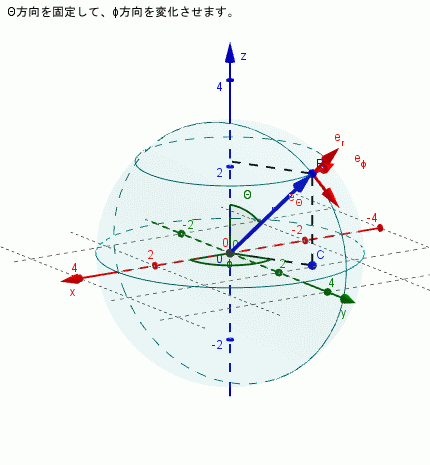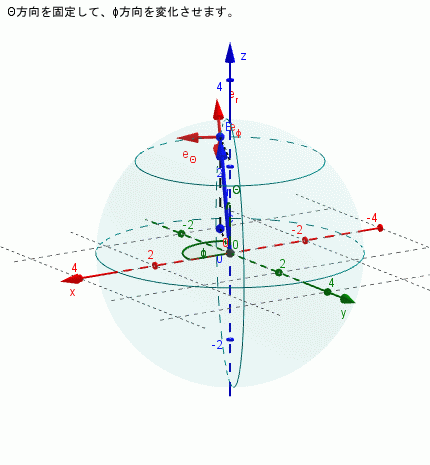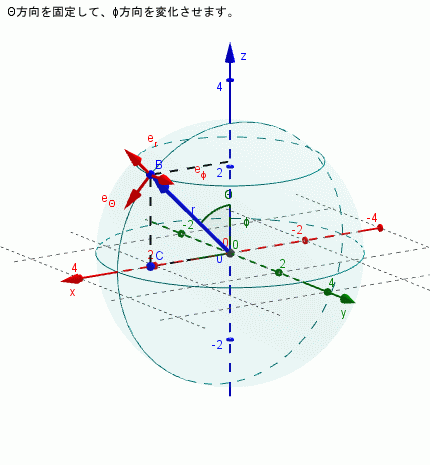
$r$のみが変化する場合、つまり$\theta$と$\phi$は時間変化しない場合は単位ベクトルの方向は変わりません。上記のことからすぐに理解できると思います。
