| (3.1) |
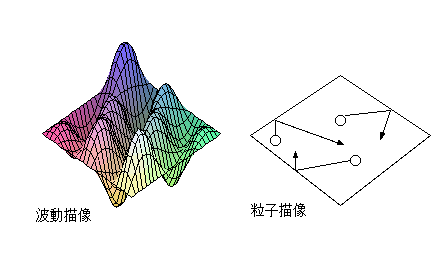 光
が粒子であると考えると、プランクが考えたような空洞の中では、光子がとびまわっていると解釈できる。分子でできた気体がそうであるように、光にも圧力が
ある。光子の圧力があることは電磁気学から理論的に導くことができるし、実験的にも確認されている。気体に圧力があるのは分子が運動量を持つからである。
したがって光子にも運動量があることになる。運動量は(質量)×(速度)のはず、と考えてしまうと「なんで光に運動量があるの?」と不思議だろう。しか
し、そもそもの運動量の定義は運動方程式[(dp)/(dt)]=Fで
あると考えたらどうだろう。こう考えれば、「力あるところには運動量の増減あり」ということになる。「光が力を出すの?」と不思議に思う人もいるかもしれ
ないが、光は電磁波、すなわち電場と磁場の波である。電場や磁場がクーロン力やローレンツ力という力を生み出すことを考えれば、光が力を出すことも当然で
ある。
光
が粒子であると考えると、プランクが考えたような空洞の中では、光子がとびまわっていると解釈できる。分子でできた気体がそうであるように、光にも圧力が
ある。光子の圧力があることは電磁気学から理論的に導くことができるし、実験的にも確認されている。気体に圧力があるのは分子が運動量を持つからである。
したがって光子にも運動量があることになる。運動量は(質量)×(速度)のはず、と考えてしまうと「なんで光に運動量があるの?」と不思議だろう。しか
し、そもそもの運動量の定義は運動方程式[(dp)/(dt)]=Fで
あると考えたらどうだろう。こう考えれば、「力あるところには運動量の増減あり」ということになる。「光が力を出すの?」と不思議に思う人もいるかもしれ
ないが、光は電磁波、すなわち電場と磁場の波である。電場や磁場がクーロン力やローレンツ力という力を生み出すことを考えれば、光が力を出すことも当然で
ある。
| (3.2) |
| (3.3) |
|
| (3.6) |
| (3.7) |
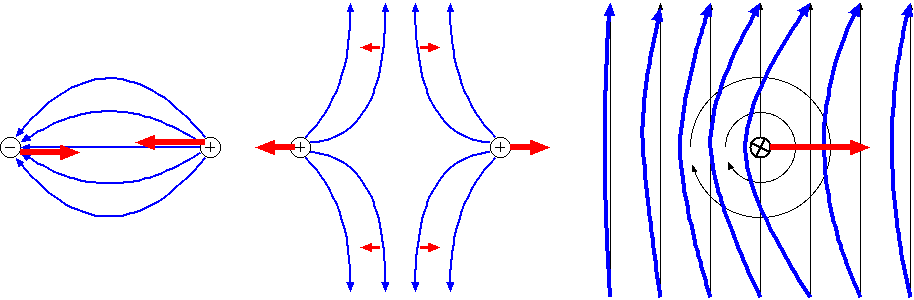 これをマックスウェルの応力と呼ぶ。この力はなじみが薄い人が多いかもしれないが、クーロン力やローレンツ力など、電磁力はすべてこの力であると解釈できる。
この力の性質は「電気力線(磁力線)はなるべく短くなろうとする。またとなりあう2本は互いに
離れようとする」とまとめることができる。そうなる理由は結局「エネルギーを下げる方向に力が働く」ということで理解できる。電気力線が短い方が、あるい
はより拡散した方がエネルギーが小さくなるのである。
これをマックスウェルの応力と呼ぶ。この力はなじみが薄い人が多いかもしれないが、クーロン力やローレンツ力など、電磁力はすべてこの力であると解釈できる。
この力の性質は「電気力線(磁力線)はなるべく短くなろうとする。またとなりあう2本は互いに
離れようとする」とまとめることができる。そうなる理由は結局「エネルギーを下げる方向に力が働く」ということで理解できる。電気力線が短い方が、あるい
はより拡散した方がエネルギーが小さくなるのである。
|
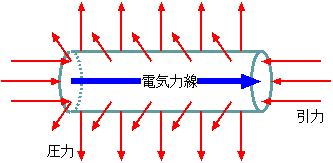 いま、ある方向に電場(電気力線)が走っているところを思い浮かべよう。この電気力線が6つの方向(±x,±y,±z)の及ぼす力のうち、2方向は引力、4方向は斥力である。今電磁波が壁のなかであっちへこっちへと飛び回っていると考えると、電気力線もいろんな方向に伸びるだろう。この時にある一つの方向に働く力を考えると、1/3の確率で引力、2/3の確率で斥力となる。結局全体の平均をとれば1/3の斥力が残ると考えられる。つまり、圧力はエネルギー密度の1/3である。
この圧力は1892年にレベデフによってはじめて実験的に確かめられている。
いま、ある方向に電場(電気力線)が走っているところを思い浮かべよう。この電気力線が6つの方向(±x,±y,±z)の及ぼす力のうち、2方向は引力、4方向は斥力である。今電磁波が壁のなかであっちへこっちへと飛び回っていると考えると、電気力線もいろんな方向に伸びるだろう。この時にある一つの方向に働く力を考えると、1/3の確率で引力、2/3の確率で斥力となる。結局全体の平均をとれば1/3の斥力が残ると考えられる。つまり、圧力はエネルギー密度の1/3である。
この圧力は1892年にレベデフによってはじめて実験的に確かめられている。