| [ | − |  2 2
2m |
( | ∂2
∂x2 |
+ | ∂2
∂y2 |
+ | ∂2
∂z2 |
) | +V(x) | ]
|
ψ = i |
∂
∂t |
ψ |
|
(16.1) |
|
(16.2) |
|
(16.3) |
|
(16.4) |
|
(16.5) |
|
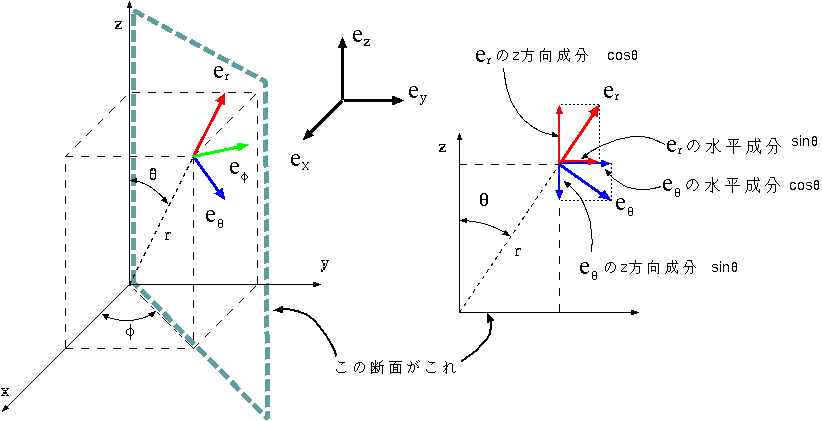
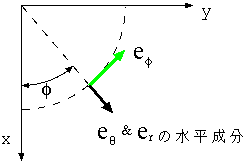 次に、上の左図を真上から見たものが右の図である。これから、→eφ
がx成分−sinφとy成分cosφを持つことがわかる。また、→erお
よび→eθは先に求めて置いた水平成分にcosφをかけた
x成分と、sinφをかけたy成分を持つこともわかる。以上をまとめて
(16.6)から(16.8)までが出る。
このベクトル演算子→∇の意味するところは、
次に、上の左図を真上から見たものが右の図である。これから、→eφ
がx成分−sinφとy成分cosφを持つことがわかる。また、→erお
よび→eθは先に求めて置いた水平成分にcosφをかけた
x成分と、sinφをかけたy成分を持つこともわかる。以上をまとめて
(16.6)から(16.8)までが出る。
このベクトル演算子→∇の意味するところは、
|
(16.9) |
|
(16.10) |
|
(16.11) |
|
(16.12) |
|
(16.13) |
|
(16.14) |
|
(16.15) |
|
(16.16) |
|
(16.17) |
|
|
(16.18) |
|
(16.19) |
|
(16.20) |
|
(16.21) |
|
(16.22) |
|
(16.23) |
|
 →x ×→∇となる。
z成分であるLzについてはz軸まわりの角運動量ということはφを変化させるという回転に対応する角運動量であるから、この角運動
量はr微分やθ微分を含まないはずである。よってφ微分に関係する部分だけを考える。たとえば[∂/∂y]は
→x ×→∇となる。
z成分であるLzについてはz軸まわりの角運動量ということはφを変化させるという回転に対応する角運動量であるから、この角運動
量はr微分やθ微分を含まないはずである。よってφ微分に関係する部分だけを考える。たとえば[∂/∂y]は
|
(16.25) |
|
(16.26) |
|
(16.27) |
|
(16.28) |
 →ez·→∇を使って計算すると、
→ez·→∇を使って計算すると、
|
(16.29) |
|
(16.30) |
|
(16.31) |
|
(16.32) |
|
(16.33) |
 →∇を代入して、→Lを極座標で計算
せよ。
さらにその自乗|→L|2を計算して、答えが
→∇を代入して、→Lを極座標で計算
せよ。
さらにその自乗|→L|2を計算して、答えが
|
|
|
|
、 |
|
|
|
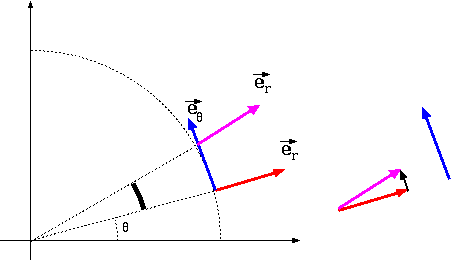 それでは納得できないならば、右の図を見
てください。
それでは納得できないならば、右の図を見
てください。