| − |  2 2
2m |
|
∂2
∂x2 |
ψ = (E−V0)ψ |
 2(k′)2)/2m]
=E−V0から決まるk′が虚数になってしまうからである。しかし、物理的状況としてはE−V0
< 0という状況だって有り得る。その場合どうなるのだろうか。もう一度シュレーディンガー方程式を解き直そう。
2(k′)2)/2m]
=E−V0から決まるk′が虚数になってしまうからである。しかし、物理的状況としてはE−V0
< 0という状況だって有り得る。その場合どうなるのだろうか。もう一度シュレーディンガー方程式を解き直そう。
|
(13.23) |
|
(13.24) |
|
(13.25) |
|
|
(13.28) |
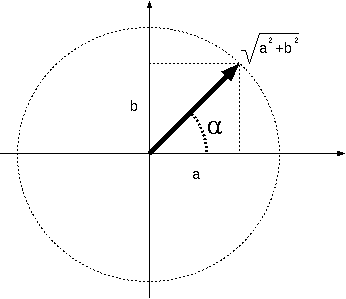 まず、Rの位相を計算しておこう。一般の複素数a+ibは
まず、Rの位相を計算しておこう。一般の複素数a+ibは
|
(13.29) |
|
(13.30) |
|
(13.31) |
|
(13.32) |
|
(13.33) |
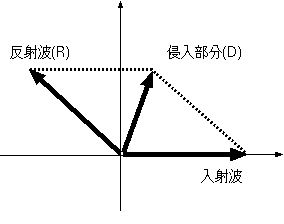 つまりこの場合、反射波の位相は−2φだけずれることになる。定義からして、φは0 < φ <
[π/2]を満たす角度(第一象限内)である。この計算でわかったように、E < V0の場合、反射波の振幅を表すRの絶対
値が1になる。つまり、結局は全部が跳ね返っていることになる。
同様に計算するとDは
つまりこの場合、反射波の位相は−2φだけずれることになる。定義からして、φは0 < φ <
[π/2]を満たす角度(第一象限内)である。この計算でわかったように、E < V0の場合、反射波の振幅を表すRの絶対
値が1になる。つまり、結局は全部が跳ね返っていることになる。
同様に計算するとDは
|
(13.34) |
|
|
(13.35) |
 )]を考えてみる。日常レベルでは、分子に出てくる量はMKS単位系でオーダー1程度だろう(1キログラム、
1ジュール)。一方分母の
)]を考えてみる。日常レベルでは、分子に出てくる量はMKS単位系でオーダー1程度だろう(1キログラム、
1ジュール)。一方分母の はMKS単位では10-33のオーダー。つまりκは1033のオーダーとなり、xが1センチのオーダーだとしてもeκxはeの1031乗ぐらい、つまりは10の1030乗ぐらいであろう。つまり、このよう
な場合でトンネル効果の起こる確率は、1の後ろに0が1030個並ぶほどの莫大な数が分母にくる数字ということになる。宇宙が終わるまで待っていても、日常生活でトンネル
効果に出会うことはありそうにない。
はMKS単位では10-33のオーダー。つまりκは1033のオーダーとなり、xが1センチのオーダーだとしてもeκxはeの1031乗ぐらい、つまりは10の1030乗ぐらいであろう。つまり、このよう
な場合でトンネル効果の起こる確率は、1の後ろに0が1030個並ぶほどの莫大な数が分母にくる数字ということになる。宇宙が終わるまで待っていても、日常生活でトンネル
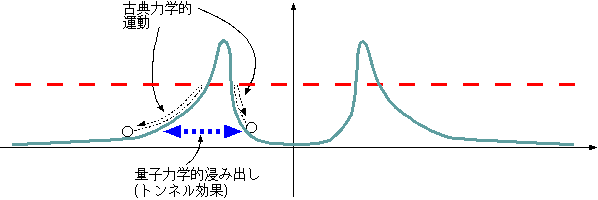
効果に出会うことはありそうにない。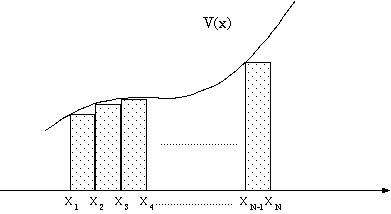 まず考えている空間x0 < x < xN
をN等分して、∆x=[(xN−x0)/N]ごとに刻む。その一区画xn
< x < xn+∆xの中ではポテンシャルV(x)が定数であると近似する(つまり、ポテンシャルを細かい階段状ポ
テンシャルで置き換える)。そうすれば波動関数の振幅は、その区画内でe−κn ∆x倍に減衰することにな
る。ただし、κn=[(√[(2m(V(xn)−E))])/(
まず考えている空間x0 < x < xN
をN等分して、∆x=[(xN−x0)/N]ごとに刻む。その一区画xn
< x < xn+∆xの中ではポテンシャルV(x)が定数であると近似する(つまり、ポテンシャルを細かい階段状ポ
テンシャルで置き換える)。そうすれば波動関数の振幅は、その区画内でe−κn ∆x倍に減衰することにな
る。ただし、κn=[(√[(2m(V(xn)−E))])/( )]である。
x=x0からx=xNまででの波動関数の減衰を考えると、
)]である。
x=x0からx=xNまででの波動関数の減衰を考えると、
|
(13.36) |
|
(13.37) |
|
(13.38) |
 ]という(日常の生活レベルにおいては)大きな数字が来ているおかげで、この
減衰は非常に速い。
なお、今行った計算は近似計算であり、厳密解ではない。一般にeF(x)のような関数を二階微分すると、
]という(日常の生活レベルにおいては)大きな数字が来ているおかげで、この
減衰は非常に速い。
なお、今行った計算は近似計算であり、厳密解ではない。一般にeF(x)のような関数を二階微分すると、
|
(13.39) |
|
 )]∫x0x√[2m
(V(x′)−E)]dx′を代入すると、
)]∫x0x√[2m
(V(x′)−E)]dx′を代入すると、
|
(13.43) |
|
|
(13.45) |
|
(13.46) |