| e±κx ただし、κ = |
 |
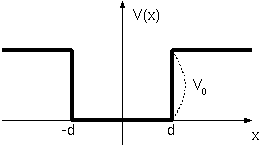 今度は、2枚の有限なポテンシャルの壁にはさまれた領域での波動関数を考えてみる。この領域を「井戸の穴」と見て「井戸型ポテンシャル」と呼ばれることが
多い。具体的には、下のようなポテンシャルの中にある質量mの粒子に対しての量子力学を考える。
今度は、2枚の有限なポテンシャルの壁にはさまれた領域での波動関数を考えてみる。この領域を「井戸の穴」と見て「井戸型ポテンシャル」と呼ばれることが
多い。具体的には、下のようなポテンシャルの中にある質量mの粒子に対しての量子力学を考える。
|
(14.1) |
|
(14.2) |
|
(14.3) |
この定理を証明するにまず、「ポテンシャルが左右対称になっている時、シュレーディンガー方程式の解ψ(x)が見つかったとすると、ψ(−x)も解であ る」ということを示す。そのために、以下のように方程式の中に出てくるxをすべて−xに置き換えた式を作る。
ポテンシャルが左右対称になっている時(V(−x)=V(x)の時)、シュレー ディンガー方程式の解は偶関数(ψ(−x)=ψ(x))であるか、奇関数(ψ(−x)=−ψ(x))であるか、どちらかである。
|
(14.4) |
|
(14.5) |
|
(14.6) |
|
(14.7) |
|
(14.8) |
|
(14.9) |
|
(14.10) |
 2 k2)/2m]=E,
[(
2 k2)/2m]=E,
[( 2
κ2)/2m] = V0−E であるから、
2
κ2)/2m] = V0−E であるから、
|
(14.11) |
 結局我々が求めるべきはκ = k tan kdとk2+κ2 = [(2mV0)/(
結局我々が求めるべきはκ = k tan kdとk2+κ2 = [(2mV0)/( 2)]
という連立方程式の解である。質量mやポテンシャルの深さV0が与えられれば、この式からk,κが計算でき、つまりは許されるエネ
ルギーEが決まることになる。
とはいえ、この連立方程式は解析的に解を求められない(式変形で答えは出せない)ので、グラフか数値計算に頼ることになる。左の図はκ =
ktankdとk2+κ2=[(√[(2mV0)])/(
2)]
という連立方程式の解である。質量mやポテンシャルの深さV0が与えられれば、この式からk,κが計算でき、つまりは許されるエネ
ルギーEが決まることになる。
とはいえ、この連立方程式は解析的に解を求められない(式変形で答えは出せない)ので、グラフか数値計算に頼ることになる。左の図はκ =
ktankdとk2+κ2=[(√[(2mV0)])/( )]の両方をグラフに書き込んだもの(もちろん、k2+κ2=[(√[(2mV0)])/(
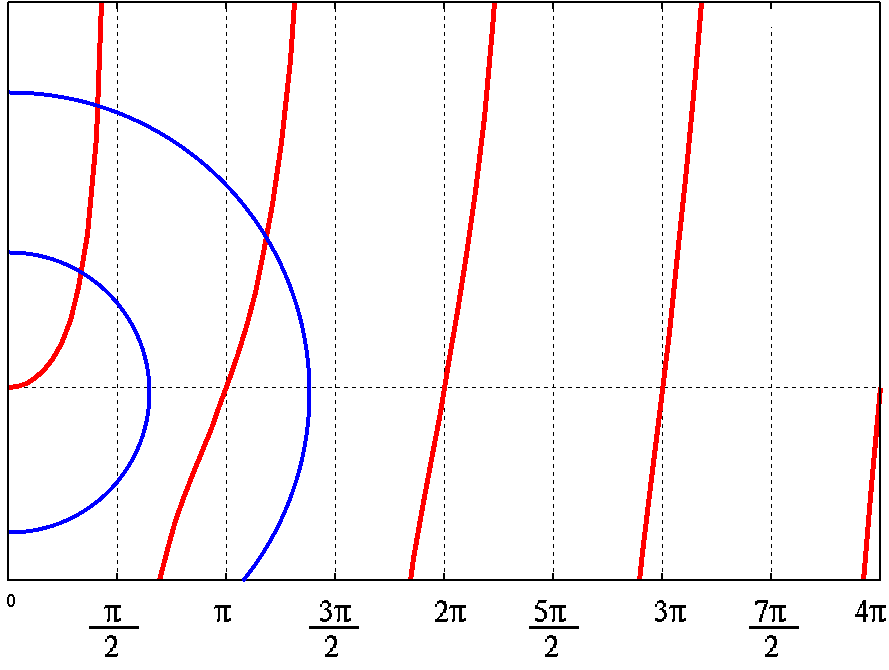
)]の両方をグラフに書き込んだもの(もちろん、k2+κ2=[(√[(2mV0)])/( )]が円の方)で、少しスケールを変えて横軸はkd、縦軸はκdになっている。タンジェントの性質により、kd=mπ(mは整数)ではκ =
0となる。グラフではκ < 0の部分も書いているが、実際にはもちろんκ > 0でなくてはならない。
図に二つの円が書いてあるが、これはV0がいろんな値をとっている場合でののk2+κ2
= [(2mV0)/(
)]が円の方)で、少しスケールを変えて横軸はkd、縦軸はκdになっている。タンジェントの性質により、kd=mπ(mは整数)ではκ =
0となる。グラフではκ < 0の部分も書いているが、実際にはもちろんκ > 0でなくてはならない。
図に二つの円が書いてあるが、これはV0がいろんな値をとっている場合でののk2+κ2
= [(2mV0)/( 2)] を表している。小さい円ではκ =
ktankdとの交点は一つしかない。一方、大きい方の円では交点は二つある。円の半径が大きくなれば(V0が大きくなれば)交点
の数はどんどん増えて行く。この交点の位置のエネルギーだけが許されるわけであるから、やはりエネルギーが量子化されていることになる。それゆえ、束縛さ
れている状態の時「離散スペクトルを持つ」とか「離散的固有値を持つ」というふうに言う。グラフの形から、かならず一つは交点があることになるが、いくつ
あるかはdやV0など、問題設定によって変わる。
2)] を表している。小さい円ではκ =
ktankdとの交点は一つしかない。一方、大きい方の円では交点は二つある。円の半径が大きくなれば(V0が大きくなれば)交点
の数はどんどん増えて行く。この交点の位置のエネルギーだけが許されるわけであるから、やはりエネルギーが量子化されていることになる。それゆえ、束縛さ
れている状態の時「離散スペクトルを持つ」とか「離散的固有値を持つ」というふうに言う。グラフの形から、かならず一つは交点があることになるが、いくつ
あるかはdやV0など、問題設定によって変わる。
|
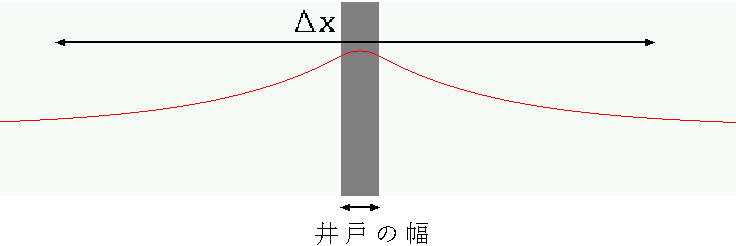 不確定性関係を使って見積もると、井戸の幅が2dなので、この中に入る波は最小でも∆p =
[h/2d]ぐらいの運動量の不確定性をもたなくてはいけない。
不確定性関係を使って見積もると、井戸の幅が2dなので、この中に入る波は最小でも∆p =
[h/2d]ぐらいの運動量の不確定性をもたなくてはいけない。