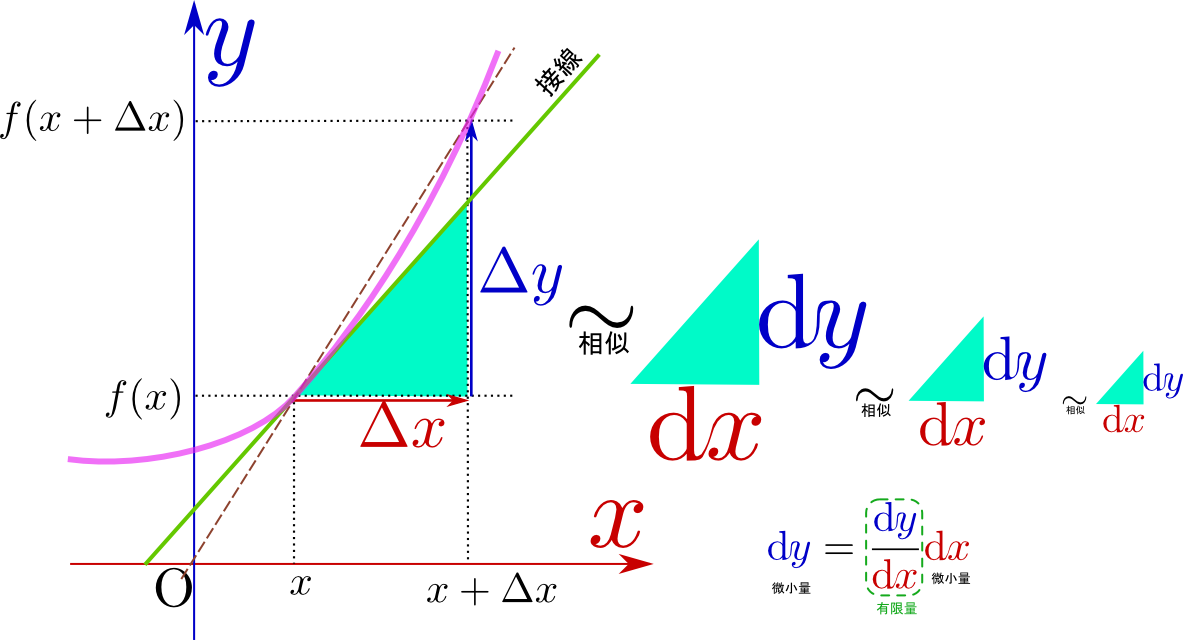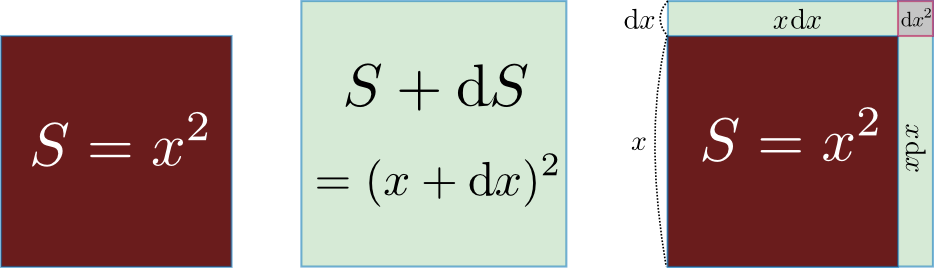2.2 微分という演算
導関数、微係数
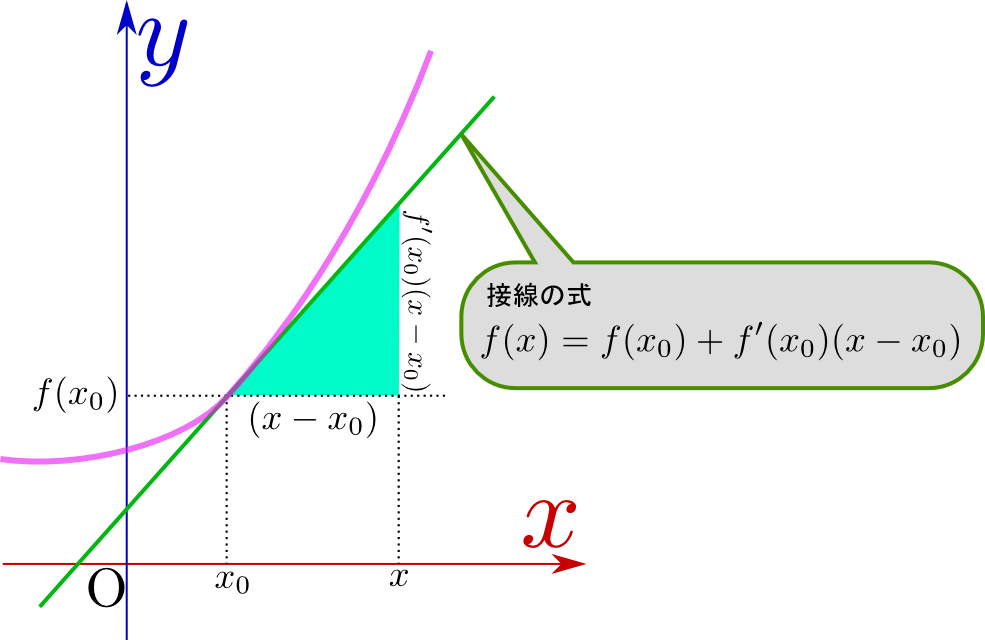
より一般的な場合で接線の式を作っておこう。一般のf(x)という関数はある点$x_0$の付近では
\begin{equation}
f(x)= a(x-x_0)+b
\end{equation}
のように直線に近似することができる。定数項bは、(両辺に$x=x_0$を代入するとわかるように)実は$f(x_0)$であり、$a$すなわち傾きは場所によって違うから、「傾きを表す関数」としてf'(x)という記号で書くことにしよう。その関数の$x=x_0$での値がaである。
これらを使えば、
\begin{equation}
f(x)=f(x_0)+ f'(x_0)(x-x_0)
\end{equation}
と書いてもよい(右辺の順番を変えたが、別に深い意味はない)。では、「傾きを表す関数」f'(x)をどう計算しよう?
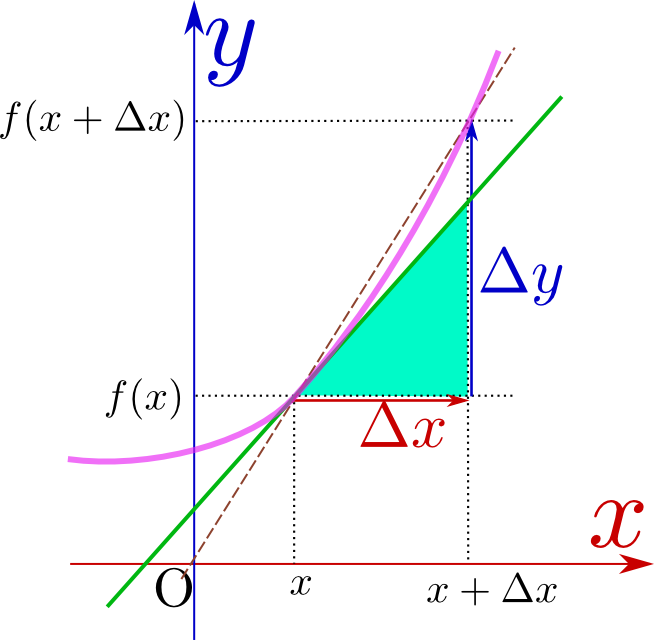
右のグラフに示したように、yの変化量${\Delta y}$は${\Delta y}=f(x+\Delta x)-f(x)$のような引き算で表現できるので、それを${\Delta x}$で割った量の${\Delta x}\to0$の極限を計算すれば、任意のxの点での傾きが計算できる。${\Delta x}$が0になるとき、二つの線が一致する、と見てよい。
$\Delta x$を0にするということは、「0で割る」という数学ではやってはいけないことをやってしまっているのではないのか??
こういう疑問を抱くのは当然である。実際に$\Delta x=0$とするのではなく、あくまで「近づける」であることに注意しよう。数学的には「極限」というのはいろいろややこしい定義をしなくてはいけないのだが、ここでは上のようにどんどん$\Delta x$を小さくしていくとどうなるかを予想した値を考えているのだと思って欲しい。そして、図でわかるように、その場合でも「直線の傾き」という量はちゃんと定義できる。
その結果もまた$x$の関数となる。その「新しい関数」を「導関数(derivative)」という名前で呼ぶ。「導関数」という言葉は元の関数f(x)から導かれた関数という意味で、
導関数の定義
$$
\underbrace{ f'(x)=\frac{\mathrm df}{\mathrm dx}(x)={\mathrm d \over \mathrm dx}f(x)}_{三通りの書き方}\equiv \lim_{{\Delta x}\to0}{f(x+{\Delta x})-f(x)\over {\Delta x}}
$$
と定義する。「導関数」は上にも書いたように、3種類の方法(本によっては別の書き方もある)で表現される。このうち後ろ二つ${\mathrm df\over\mathrm dx}(x),{\mathrm d \over \mathrm dx}f(x)$の持つ意味については、後で述べる。
関数f(x)からその導関数f'(x)を求める計算(たとえば$f(x)=x^2$から$f'(x)=2x$)を、「微分する」と表現する。以下のように書いてもよい。
\begin{equation}
f(x + {\Delta x})=f(x)+ f'(x){\Delta x}+{\cal O}(({\Delta x})^2)
\end{equation}
ここで使われた${\cal O}(a^n)$という記号(ランダウの記号)について説明しておこう。
今ある数が${\Delta x}\to0$において0にならないとすると、これは${\cal O}(1)$と言う。またある量$A$が${\Delta x}$で割ってから${\Delta x}\to0$にすると0でない値に収束するとき(つまり、${A\over {\Delta x}}$が0でない値に収束するとき)、${\cal O}({\Delta x})$だ、と言う。同様に、$({\Delta x})^n$で割ってから${\Delta x}\to0$の極限を取ると0でないとき、${\cal O}(({\Delta x})^n)$だ、という。簡単な例を示す。
\begin{equation}
(x+{\Delta x})^3 = \underbrace{x^2}_{{\cal O}(1)}+\underbrace{3x{\Delta x}
+\underbrace{3x({\Delta x})^2
+\underbrace{({\Delta x})^3}_{{\cal O}(({\Delta x})^3)}
}_{{\cal O}(({\Delta x})^2)}}_{{\cal O}({\Delta x})}
\end{equation}
$3x({\Delta x})^2$だけではなく$3x({\Delta x})^2 + {\Delta x}^3$全部が${\cal O}(({\Delta x})^2)$である(${\cal O}({\Delta x})$も同様)であることに注意しよう。${\cal O}(({\Delta x})^n)$のなかには、$n$より大きいオーダーの項${\cal O}(({\Delta x})^m)~~(m>n)$が含まれていてもよい。
オーダーは「桁」を意味する英語である。イメージとして、${\Delta x}$の値を$0.1,0.01,0.001,\cdots$とどんどん小さくしていった場合を考えると、
| ${\Delta x}$ | 0.1 | 0.01 | 0.001 | $\cdots$ |
| $({\Delta x})^2$ | 0.01 | 0.0001 | 0.000001 | $\cdots$ |
| $({\Delta x})^3$ | 0.001 | 0.000001 | 0.000000001 | $\cdots$ |
のように小さくなっていく。${\Delta x}$も$({\Delta x})^2$も桁が小さくなっていくが、$({\Delta x})^2$の方が(桁違いに!)小さいということがわかる。これが「オーダーが違う」という意味である。
しかしまで具体的に「オーダーって何?」という顔をしている人がいたので、黒板に下のような式(表)を書いた。
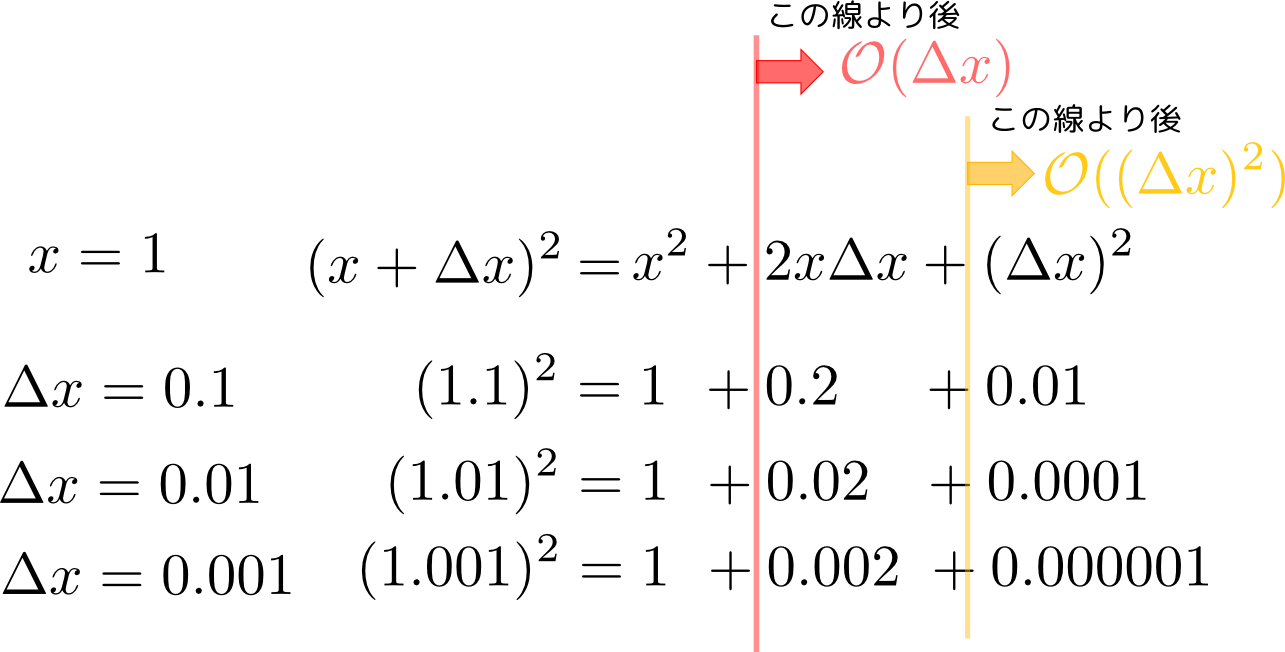
↑の図を見ると、${\cal O}(\Delta x)$と${\cal O}((\Delta x)^2)$が「桁が違う」という意味で「違う大きさ」なのが実感できるのではないかと思う。
以上のように、
微分の二つの表現
$$
\begin{array}{rcl}
f'(x)&=& \lim_{{\Delta x}\to0}{f(x+{\Delta x})-f(x)\over {\Delta x}}\\
f(x + {\Delta x})&=&f(x)+ f'(x){\Delta x}+{\cal O}(({\Delta x})^2)
\end{array}
$$
のような二通りの方法で微分という演算を記述できる。
最後の項${\cal O}(({\Delta x})^2)$は、${\Delta x}$で割ってから${\Delta x}\to 0$の極限を取ると消えてしまう項である(だから、極限を取った後の\式{bibunteigi}には登場しない)。
\begin{equation}
\begin{array}{rll}
f(x + {\Delta x})=&f(x)+ f'(x){\Delta x}+{\cal O}(({\Delta x})^2)&\\
f(x + {\Delta x})-f(x)=& f'(x){\Delta x}+{\cal O}(({\Delta x})^2)&\\
{f(x + {\Delta x})-f(x)\over {\Delta x}}=& f'(x)+\underbrace{{{\cal O}(({\Delta x})^2)\over {\Delta x}}}_{極限で消えてしまう項}
\end{array}
\end{equation}
という操作により二つの式がつながる。
$f(x + {\Delta x})=f(x)+ f'(x){\Delta x}+{\cal O}(({\Delta x})^2)$の形では、$f'(x)$は
f(x)の中の$x$が${\Delta x}$変化した時の、f(x)の変化量$\left(f'(x){\Delta x}\right)$の、${\Delta x}$の前の係数
であると言える。よって$f'(x)$を「微係数(differential coefficient)」と呼ぶこともある。
以上からわかるように「導関数」と「微係数」は同じものを指す。二つの違いは、「関数から作った、新しい関数(導関数)」と考えるか、「関数を${\Delta x}$が小さいところで展開すると出てくる係数(微係数)」と考えるかの違いである。
$\mathrm d $という記号
${\Delta x}$や${\Delta y}$は「変化量」という意味があった。微分を行う時は、${\Delta x}$を0に近づける(連動して、${\Delta y}$も0に近づく)。このようにここから先の計算ではしばしば、${\Delta x}$や${\Delta y}$に「変化量」という意味に加えて「0に近づく」という属性が加わる。この「0に近づけていく変化量」という量を表すために、新しい記号として$\mathrm dx,\mathrm dy $を導入しよう。つまり、$\Delta$の替りに$\mathrm d $という記号を使って後で$\to0$という極限を取ることが約束されている変化量を示すことにする。本講義で$\mathrm dx $とか$\mathrm dy$ のように$\mathrm d $のついた量は、すべて「微小変化」を表現する量である。
$\mathrm dx$や$\mathrm dy$を「微小変化」と呼ぶが、この呼び方は少し説明が不足していて、単に「微小」ではなく「0になる極限を取る」という点が重要である。
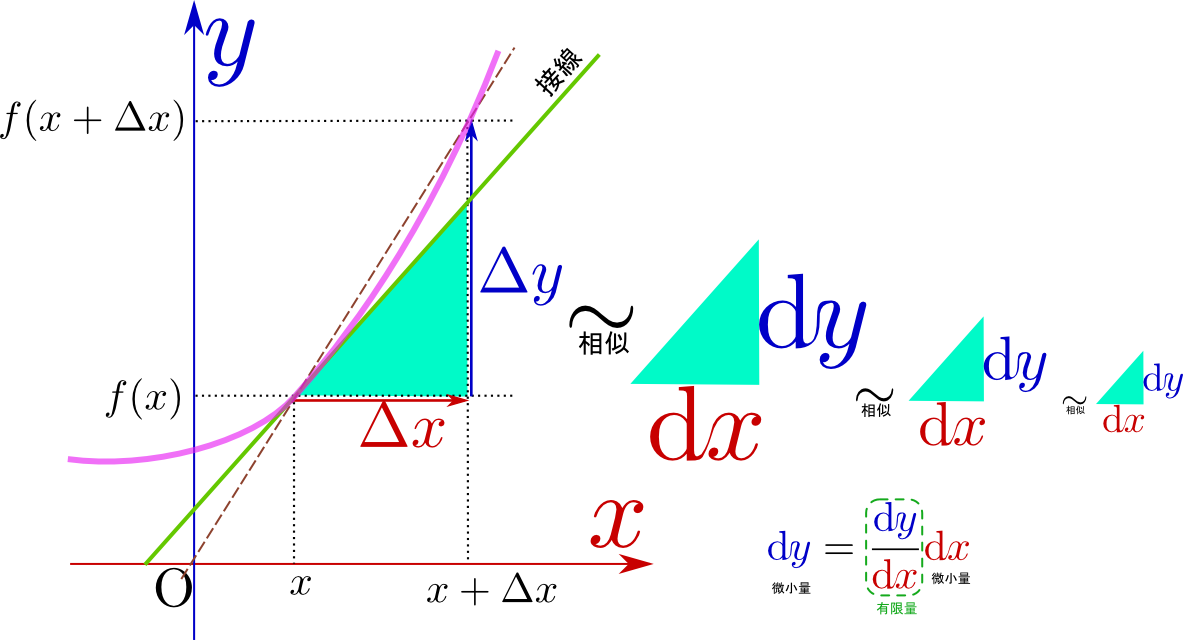
あるいは「微小」という考え方がしっくりこない、という人は以下のように考えてもよい。
上の図にも示したように、$\mathrm dx$や$\mathrm dy$はあくまで、 のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える(この考え方なら微小である必要はない)。そして、$\mathrm dx$ や$\mathrm dy $そのものの大きさは重要ではなく、
のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える(この考え方なら微小である必要はない)。そして、$\mathrm dx$ や$\mathrm dy $そのものの大きさは重要ではなく、 という形(どんな直角三角形か?)、あるいは「$\mathrm dx$ と$\mathrm dy $の比」が重要であって、$\mathrm dx$ や$\mathrm dy $そのものは大きさを考えてはいけない(考えても意味はない)量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy $の二つで向きを表現する量」なのである。
という形(どんな直角三角形か?)、あるいは「$\mathrm dx$ と$\mathrm dy $の比」が重要であって、$\mathrm dx$ や$\mathrm dy $そのものは大きさを考えてはいけない(考えても意味はない)量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy $の二つで向きを表現する量」なのである。
${\mathrm dy\over \mathrm dx}$は普通の数(大きさを考える意味がある)だし、$\mathrm dy=a\mathrm dx$と書いた時の$a$も普通の数である。だから${\mathrm dy\over \mathrm dx}=2$や$\mathrm dy = 0.7\mathrm dx$は意味のある式である。しかし、$\mathrm dx=1$とか$\mathrm dy=0.02$などという式には全く意味がない。$\mathrm dy$ や$\mathrm dx $は、二つがペアになって接線の向きを表現している量であって、$\mathrm dx$ のみの大小を云々してはいけない。
新しい記号を使えば、接線の傾きは${\mathrm dy\over \mathrm dx}$になる。この${\mathrm dy\over\mathrm dx}$、厳密に書けば
\begin{equation}
{\mathrm dy\over\mathrm dx}=\lim_{{\Delta x}\to0}{{\Delta y}\over {\Delta x}}
\end{equation}
が導関数(もしくは微係数)である。$\mathrm dy$ と$\mathrm dx $は微小量、すなわち0になる極限を取るべき量だが${\mathrm dy\over \mathrm dx}$は有限な量である。
こうして「傾き」という量を$x$の関数として表現する方法を我々は得た。最初に書いた${{\Delta y}\over {\Delta x}}$という量は、ある「幅」${\Delta x}$があって(その「幅」の間での変化の割合として)初めて定義できる量だったが、${\mathrm dy\over \mathrm dx}$の方は、「一点」$x$で決まる量であることに注意しよう。
これで${\mathrm dy\over \mathrm dx}$という量が「接線の傾き」という数字として意味のある量となったので、${\mathrm dy\over \mathrm dx}$で一つの量、として扱うことにする。この量もまた$x$の関数であることを表現するため、${\mathrm dy\over \mathrm dx}(x)$のように$(x)$という引数を付けて書く。この書き方はf(x)の$f$のところに${\mathrm dy\over \mathrm dx}$が入った形で、${\mathrm dy\over \mathrm dx}$が「関数名」として機能している(だから、${\mathrm dy\over \mathrm dx}$で1文字であるかのごとく扱う)。
これが導関数(もしくは微係数)を${\mathrm dy\over \mathrm dx}(x)$のように書く理由である。f'(x)の方はニュートンによる記号で、$f$という関数から$f'$を作ったということをよく表現できている記号である。一方${\mathrm dy\over \mathrm dx}$はライプニッツの記号で、何の変化と何の変化の比を考えているのかがよく表現できている記号である。これらの記号は使いどころによって一長一短がある。
$\mathrm dy=f'(x)\mathrm dx$とした時、$f'(x)={\mathrm dy\over \mathrm dx}(x)$であるが、これを${\mathrm df\over \mathrm dx}(x)$と書くこともある(関数を意味する$f$を変数の意味にも使っている)。$\mathrm dy={\mathrm df\over \mathrm dx}(x)\mathrm dx$と書いた場合、導関数を求めるという計算$f(x)\to f'(x)$は、$f(x)\to {\mathrm df\over \mathrm dx}(x)$となる。この計算は、あたかも、「f(x)に${\mathrm d \over \mathrm dx}$が掛かった」ように見える。そこで、同じ式を$f(x)\to {\mathrm d \over \mathrm dx}f(x)$と書くこともある。
この${\mathrm d \over \mathrm dx}$のような記号を「\newwordE{びぶんえんざんし}{微分演算子}{differential operator}」と呼ぶ。
「演算子(operator)」とは「関数を別の関数に変える操作を表現したもの」である。
微分演算の簡単な例
この新しい記号を使って微分の計算を行ってみよう。
前に行った$f(x)=x^2$の微分を例としよう。まず、$ {\Delta y}=2{x\Delta x}+({\Delta x})^2$を
\begin{equation}
\mathrm dy=2x\mathrm dx+(\mathrm dx)^2
\end{equation}
と書きなおす。この式の$\mathrm dx\to0,\mathrm dy\to0$の極限を考えると
\begin{equation}
\underbrace{ \mathrm dy}_{\to0} = \underbrace{2x\mathrm dx}_{\to0} + \underbrace{(\mathrm dx)^2}_{\to0}
\end{equation}
となって0=0という「当たり前すぎてつまんない(trivialな)式」が出る。何の情報も引き出せない。$\mathrm dy$と$\mathrm dx$の比のみが重要なのだから、まず両辺を$\mathrm dx$で割って
\begin{equation}
{\mathrm dy\over\mathrm dx} = 2x + \mathrm dx
\end{equation}
とした後に$\mathrm dx\to0$という極限を取ることで、以下の式を得る。
\begin{equation}
{\mathrm dy\over\mathrm dx} = 2x
\end{equation}
「$\mathrm dx$というのは$\mathrm dx\to0$という極限を取られることを運命づけられている量であることを考えると、右辺第二項の$(\mathrm dx)^2$をこれ以上計算する必要はない」と考えて
\begin{equation}
\mathrm dy= 2x\mathrm dx
\end{equation}
として${\mathrm dy\over\mathrm dx}=2x$を出してもよい。というより慣れてきたらそうするべきである。
$2x\mathrm dx$も$(\mathrm dx)^2$も、$\mathrm dx\to0$とすれば$0$になるのは同じなのに、$(\mathrm dx)^2$の方だけを消す理由は何ですか?
$2x\mathrm dx$と$(\mathrm dx)^2$を比較して、「$(\mathrm dx)^2$の方が速く0になる」という判断で消す。具体的には$\mathrm dx$の次数を考える。$2x\mathrm dx$は$\mathrm dx$の1次、$(\mathrm dx)^2$は$\mathrm dx$の2次である。\式{A3}のような形が最後に出てくることを考えると、$\mathrm dx$の次数が1次の量と2次の量があれば、1次の量(\式{A3}の段階では0次の量になっている)だけが最後に残り、2次の量(\式{A3}の段階では1次の量)は消していい。
あくまで「小さい物+もっと小さい物」という形になっている時に「もっと小さい物」の方が消せるのだ、ということに注意しよう。
「何が小さいか」、つまり「何が消せるか」はあくまで「全体との比較」で決まることに注意しよう。たとえば国家予算の話をしている時には100円なんて無視していいが、今日の昼御飯何を食べるか考えている時には、100円の差は大きい。
上で$x^2 + 2x\Delta x + (\Delta x)^2$という三つの項を考えたが、これはそれぞれ10000円、100円、1円だと思っておけばよい。「10000円あるなら100円を忘れてもいいんじゃないのか?」と思うかもしれないが、この計算において$x^2$は「いずれ左辺と右辺で打ち消し合って消える量」である。つまり「友達に借金があって、明日10000円返さなくてはいけない」という状況で10000円と100円と1円を持っている。このときは100円すなわち$2x\Delta x$は重要である(明日ジュース1本ぐらいなら飲める)。一方その状況でも1円の意味は少ない。
このようにして消される量は「高次の微小量」と呼ばれる。このような時も「$\mathrm dx$と$(\mathrm dx)^2$はオーダーが違う」という言い方をする。$2x\mathrm dx$は「$\mathrm dx$ の1次のオーダー」、$(\mathrm dx)^2$は「$\mathrm dx$ の2次のオーダー」である。今の場合オーダーが高いほど小さいので、次数が一番低いオーダー(今は1次)の量だけを考えておけばよい。2次が一番低いオーダーの時は2次を残して3次以上を無視する。何がなんでも2次を無視するのでははなく、「考えている中でもっとも低いオーダーのみを残す」というルールで考える。
以下で「慣れた人」の考えの手順を述べよう。$y=x^2$の両辺を微小変化させると
\begin{equation}
y+\mathrm dy = (x+\mathrm dx)(x+\mathrm dx)
\end{equation}{
になる。そして「あ、この中には$x\mathrm dx$が2個あるな」と考えれば、右辺は$x^2+2x\mathrm dx$となる。
あるいは「さらに慣れた人」は以下のように考える。
左辺は$y$が$\mathrm dy$だけ変化する。右辺は$x$が$\mathrm dx$だけ変化するが、$x$が二つあるので、
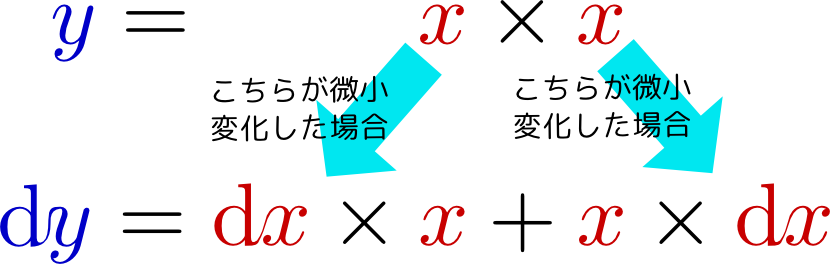
のように変化すると考えれば、$\mathrm dy=2x\mathrm dx$が出てくる。この計算(左辺においては$y\to\mathrm dy$、右辺においては$x^2\to 2x\mathrm dx$)のことを「両辺を微分する」と表現する。
用語が少し混乱しているのだが、
- 式$y=x^2$から、その微小変化の式$\mathrm dy=2x\mathrm dx$を作る(「$y=x^2$の両辺を微分すると、$\mathrm dy=2x\mathrm dx$」)。
- 関数$y=x^2$から、$y$の導関数${y'}=2x$を導く(「$x^2$を$x$で微分すると$2x$」)。
のどちらも「微分する」と表現するので注意しよう。
次に図解で考えよう。一辺$x$の正方形の面積Sは$S=x^2$という式で表現できる。この式を微分した結果の導関数が${\mathrm dS\over \mathrm dx}(x)=2x$であることは、
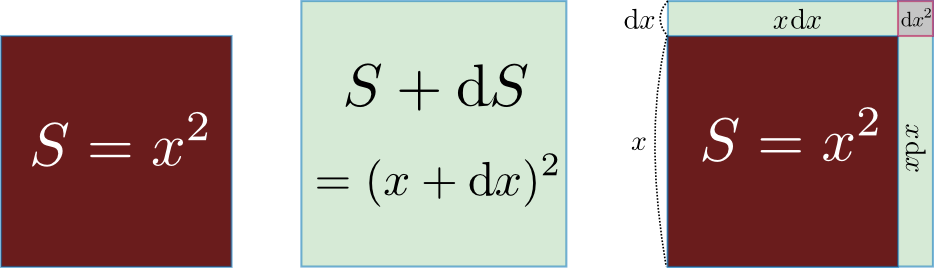
という図から理解できる。この場合、正方形の「縦」の変化による面積変化$x\mathrm dx$と、「横」の変化による面積変化$x\mathrm dx$の足算が面積変化$2x\mathrm dx$となっている。$\mathrm dx^2$の部分は無視されている。
$y=x^3$の微分を図で考えるとすると立方体が大きくなるところを想像するとよい(やってみよう)。
 のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える(この考え方なら微小である必要はない)。そして、$\mathrm dx$ や$\mathrm dy $そのものの大きさは重要ではなく、
のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える(この考え方なら微小である必要はない)。そして、$\mathrm dx$ や$\mathrm dy $そのものの大きさは重要ではなく、 という形(どんな直角三角形か?)、あるいは「$\mathrm dx$ と$\mathrm dy $の比」が重要であって、$\mathrm dx$ や$\mathrm dy $そのものは大きさを考えてはいけない(考えても意味はない)量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy $の二つで向きを表現する量」なのである。
という形(どんな直角三角形か?)、あるいは「$\mathrm dx$ と$\mathrm dy $の比」が重要であって、$\mathrm dx$ や$\mathrm dy $そのものは大きさを考えてはいけない(考えても意味はない)量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy $の二つで向きを表現する量」なのである。