受講者の感想・コメント
青字は受講者からの声、赤字は前野よりの返答です。
0で割ってもいいということが意外だった。
お金のたとえがわかりやすかった。小さい数を考えないことで計算もわかりやすくなるし、答えもあまり変わらないのですごいと思った。
いやいやいや! 「割ってもいい」なんて一言も言ってないぞ!!!
「0に近づける」だけで0にするわけじゃないから問題ない、という話をしたはず。
微分を面積で考える!!とてもおもしろい!!今まで${\mathrm dy\over \mathrm dx},{\mathrm d\over \mathrm dx}f(x)$のい意味が分からなかったのですが、よく分かりました!!
図形でイメージするってのはとても大事。
微分の表し方は今までに知らなかった方法もあるということを知った。オーダーという新しい記号も出てきたので、しっかり復習して、理解を深めたい。
それぞれの表し方の得意分野があるので、いろいろ使ってみてあげてください。
微分の式のことを形しか覚えてなかったので、改めて、こういう手順でやるということを思いさらされました。
形だけではなく、意味と「心」を知りましょう。
微分について、理解できた。微小量の変化を図などを用いてよくわかった。
じっくり図を自分でも描いてみてください。
文系の友達に聞いてみたところ、「逆関数って何?」って言われました(←先週、「指数関数が対数関数だって知らない人もいるのでは」と書いていた人)。
微分の概念がわかりやすくなったと思います。
なるほどそこまでとんでましたか>逆関数。
微分の概念はよく理解しておきましょう。
よくax+bx=(a+b)xを子供に教える時に面積を使いますが、微分も面積(誤差が微妙にあるので、子供にわかるかは別ですが)示せるというのは発想が面白かったです。
図形的な考え方ってのは大事ですよ。
答は「媒介」するものがあることです(←先週、「物質はどう結合するか」という質問をしていた人)。
${\cal O}$(オーダー)ってのは初めて見た。学食の白身フライの卵あんかけがとても好きです。日常でみかける形を関数で描いたものを見ると「おお!」となりますね。
なるほど>媒介するもの。
白身フライのあんかけ??(はてどこに出てきたのか?)
微分の考え方がわかった。
それはよかった。
導関数などへの新しい見方がわかってとても楽しかった!
微分の気持ちをわかっていきましょう。
ランダウの記号が、物理学基礎演習にもあって意味が分からなくて困っていたけど、今日の説明でわかった。
これからも使いますよ。
物理で使う微分は数学ほど細かくなくてもいいんだなと思った。
物理で使う関数は「おとなしい関数」が多いので、神経質にならなくても大丈夫、ってことはあります。
高校の微分と違っていろんな記号が出てきたけどそれを使うといろんな微分の仕方ができてとても楽しかった。
それぞれ、便利なやり方です。
今まで${f(x+h)-f(x)\over h}$の形でしか微分したことがなかったが別の形もあることを知った。
今後はいろいろ使っていきます。
オーダーΔxがΔxで割ったら0になるのには驚いた。微係数は初めて知った。
ならないならない!(なんか聞き間違えている)。オーダーΔxをΔxで割ったら0ではない有限な数です。
$S\to S+\mathrm dS$の面積変化から、微分を再確認できました。
図で考えるのも楽しいですね。
微分の違うやり方を知った。このやり方をしっかりできるようにしたい。
練習していきましょう。
後半の内容が最初はわかりませんでしたが、途中で理解できました。
わからなかったらすぐ質問する!
${\cal O}(1),{\cal O}(\Delta x)$との相互効果で${\mathrm dy\over \mathrm dx}$が何となくわかってきた。
「なんとなく」では今後困るので、「完璧」にしてください。
新しい記号とかもでてきたので、はやくなれていきたい。
どんどん使いましょう。そうすると自動的に覚える。
導関数の式は知ってましたが微係数の式は知らなかったです。お金に例えるのがわかりやすかったです。
みんなお金だと現実的に考えられるのかなぁ。
高校までの勉強で曖昧だったところがちゃんと理解できた。今回の講義はとても大事だと思った。
曖昧さのないかたちで理解していきましょう。
${\cal O}$を初めて習ったと思います。
タブレットが切れてました。
タブレットなら前に余ってましたよ。なぜ授業中にそれを言わないの??
微分の式がちょっとイメージできた。
「オーダー」が初めてきいたのでおもしろかった。
「オーダー」はこれからも使っていきます。
微分はなにをやっているのかわかった。ありがとうございます。
わかってくれてよかった。次からどんどん使っていきましょう。
${\cal O}$について初めて学んだ。少し難しかったが、理解できたと思う。今回学んだことを忘れないようにしたい。
どんどん使っていきましょう。そうすれば忘れるひまもない。
今までは${\mathrm dy\over \mathrm dx}$は微分という考えだったが、dyとdxのちゃんとした意味が理解できてよかった。
いや、そうじゃなくて今日やったのこそが「微分という考え」そのものなんです。
タブレットを使って極限の傾きを見たとき、頭ではわかっていたけれど、目で見ることでこんなに理解するものかとおどろいた。また、最後の微分で今までと違うやり方で色々なやり方があるんだなと思った。
視覚的体験ってのは大きいですね。タブレットがない時でも頭の中でイメージを作るようにしてみてください。
自分の知らなかった微分の計算をしておもしろかった。わかりやすかった。
新しいやりかたを身につけていきましょう。
テイラー展開に似ているなと思った。つながる話だと思うので、柔軟な考えをもって応用につなげていきたいです。
もちろん、テイラー展開は微分と深くつながってます。
今日は微分を本格的にやった。復習してしっかり身につけようと思った。
「本格的」なのは、実は次あたりからです。
今日の微分は少し難しかったので、復習してしっかりと理解していきたいです。
じっくり復習しておいてください。
微分の意味とか計算を学べてよかったです。今まで公式として使っていた導関数とかも、意味を改めて知ることができたので良かったです。
意味を考えながら、使っていきましょう。
微分の意味がよくわかりました。新しい文字とか出てきて楽しかったです。${\mathrm dy\over \mathrm dx}$の読み方間違えていたので気をつけます!
わかってくれてよかった。読み方は注意。
微分を図で見たら自分の中でいろいろつながっておもしろかった。
つながりは大事ですね〜〜〜。
微分のことが詳しくわかってよかった。微分の仕組みがわかった。
じっくり理解しておきましょう。
微分で新たに${\cal O}$という文字がでてきた。早くマスターしたい。
微分だけでなくいろんなところで使います。
オーダーのところのプリントが欲しいなと思った。
プリントにもだいたいのことは書いてありますよ。
具体的な数字を使ってみると、${\cal O}$などを理解するのが簡単になったので、他の場面でわからなくなった時も、具体的な数字を入れて考えてみようと思いました。
いいことですね! 是非、試してみてください。
微分はとてもよかった。今日は暑くなかった。
暑くなってもしっかり理解していこう。
最初は数式の意味が全然わからなかったけど、先生が具体的な数字を代入したり、お金の話をしてくれたりしたので、理解できた。
やっぱり具体的な話は(お金も)大事だな〜。
今回は、今まで知らなかった微分のことがわかり、微分のことがさらにわかりよかった。
それはよかったです。
$y=x^n$を$y+dy=(x+dx)^n$として計算することで高校で使っていた公式が出てきたのはおもしろかった。
高校で使っていた式も(多少見た目の手順は違っても)同じ方法で出してるんですよ。
今日は微分について詳しく勉強しました。性質を知ることができてよかったです。
まだまだ知るべきことはたくさんあります。がんばっていきましょう
微分の定義がわかった。お金のたとえがわかりやすかった。
やっぱりお金が一番わかりやすいのかな。
${\Delta y\over \Delta x}=2x+\Delta x,\lim_{\Delta x\to0}{\Delta y\over \Delta x}=2x$は面白い!!と思いました。長年$f'(x)=2x$がどこから出てきたのかわからなかったので、感動しています。
本当のところ、それはもっと前からわかっているべきなのだけど、とりあえず今わかって感動してくれて、とてもうれしい。
お金に例えると途端にわかるようになるのはなぜでしょうか。
皆さん真剣味が増すんでしょうか(^_^;)。
${\cal O}$の話でお金に例えられるとわかりやすかった。
やはり、現実的な話ほどわかりやすい…のかな。
オーダーの説明のとき、お金にたとえたのがおもしろかったです。
何か説明する時はお金に例えるに限るなぁ。
スッキリ
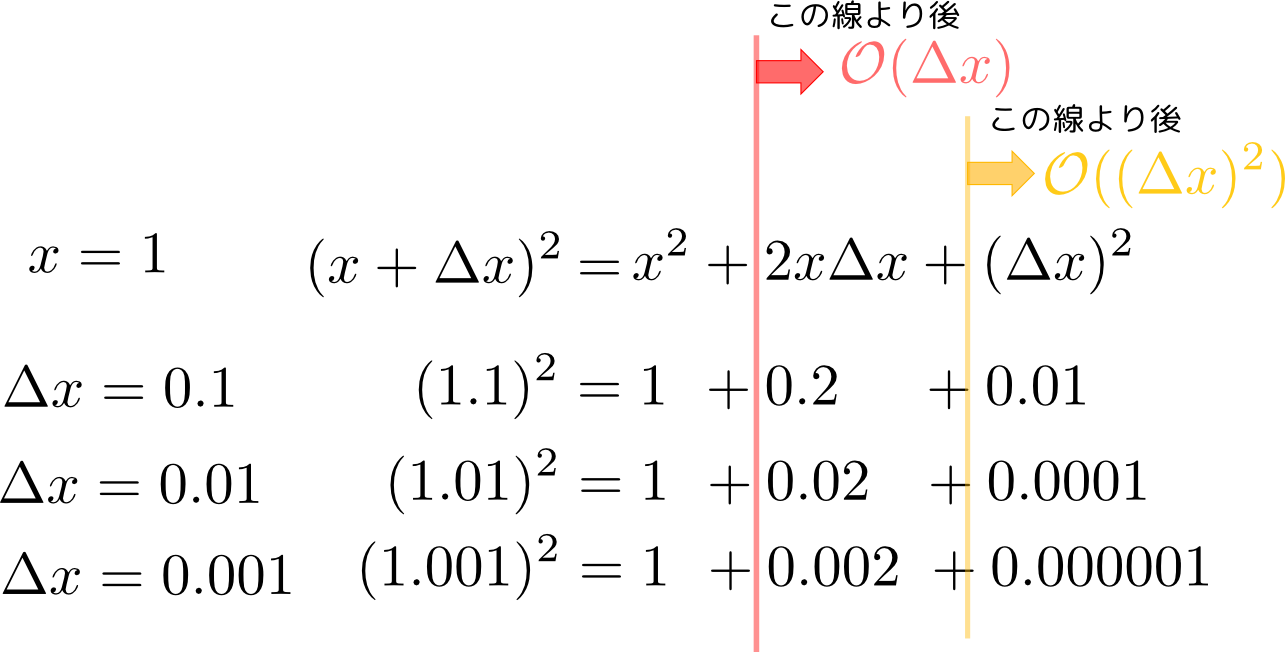
具体的な計算で確認するのが一番ですね。
