|
|
| (7.4) | |||||||||||||
|
|
| (7.5) |
| (7.1) |
| (7.2) |
| (7.3) |
 ]×(古典力学的作用)であり、解析力学とつながりのあるものであることはすでに述べた。シュレーディンガーもこのつながりをヒントに方程式の形を決めている。
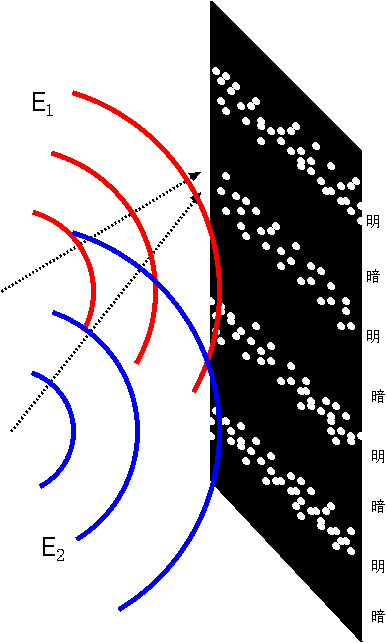
(7.3)で表される波は平面波であって、宇宙の端から端まで同じ振幅で振動している波である。実際にできるのはこれらの波のいろんな波長のものを足し算したものになるであろう。
今からつくる方程式は線形方程式(変数に関して1次の量のみを含む方程式)であることを要求する。線形であれば、解の重ね合わせができる。つまり、Aという解とBという解を見つけたならば、αA+βB(α,βは適当な定数)も解である。したがっていろんなλに対してψλ を求めれば、その重ね合わせでさらにたくさんの解を作ることができるであろう。これを「重ね合わせの原理」(principle of superpostion)と呼ぶ。電磁場や、音などの波には重ね合わせの原理が成立する36。ここまで考えてきたことからすると、重ね合わせの原理は量子力学でも成立していて欲しい。
逆に重ね合わせの原理が満たされているならば、複雑な波も簡単な平面波の重ね合わせで表現できるということになるので、とりあえず平面波をとりあげて考えていけばよいことになる。
というわけで一つの関数ψλを考えるわけだが、この前では
]×(古典力学的作用)であり、解析力学とつながりのあるものであることはすでに述べた。シュレーディンガーもこのつながりをヒントに方程式の形を決めている。
(7.3)で表される波は平面波であって、宇宙の端から端まで同じ振幅で振動している波である。実際にできるのはこれらの波のいろんな波長のものを足し算したものになるであろう。
今からつくる方程式は線形方程式(変数に関して1次の量のみを含む方程式)であることを要求する。線形であれば、解の重ね合わせができる。つまり、Aという解とBという解を見つけたならば、αA+βB(α,βは適当な定数)も解である。したがっていろんなλに対してψλ を求めれば、その重ね合わせでさらにたくさんの解を作ることができるであろう。これを「重ね合わせの原理」(principle of superpostion)と呼ぶ。電磁場や、音などの波には重ね合わせの原理が成立する36。ここまで考えてきたことからすると、重ね合わせの原理は量子力学でも成立していて欲しい。
逆に重ね合わせの原理が満たされているならば、複雑な波も簡単な平面波の重ね合わせで表現できるということになるので、とりあえず平面波をとりあげて考えていけばよいことになる。
というわけで一つの関数ψλを考えるわけだが、この前では
|
|
 [∂/∂t]も、同様に運動量や座標と関係付けられるはずである。その関係を、波動方程式の形で表したものがシュレーディンガー方程式なのである。
非相対論的な古典粒子の場合、E=H=[1/2m]|→p|2+V(x)であるから、そのような粒子を表す波は
[∂/∂t]も、同様に運動量や座標と関係付けられるはずである。その関係を、波動方程式の形で表したものがシュレーディンガー方程式なのである。
非相対論的な古典粒子の場合、E=H=[1/2m]|→p|2+V(x)であるから、そのような粒子を表す波は
| (7.8) |
| (7.9) |
| (7.10) |
 [∂/(∂qi)]と置き換えたうえで
[∂/(∂qi)]と置き換えたうえで
| (7.11) |
| (7.12) |
 ]×(作用)が波動関数ψのexpの肩に乗っていると思えば、φに対する運動量である角運動量pφは、−i
]×(作用)が波動関数ψのexpの肩に乗っていると思えば、φに対する運動量である角運動量pφは、−i [∂/∂φ]のように置き換えられることになる。その他の一般座標も同様である。曲線座標に対する運動量の中には単純に−i
[∂/∂φ]のように置き換えられることになる。その他の一般座標も同様である。曲線座標に対する運動量の中には単純に−i [∂/∂X]と表すことができない場合があるが、それに関してはまた後で述べよう。
この考え方からすると、ボーア・ゾンマーフェルトの量子化条件∫p dq = nhは、以下のように考えることができる。p=−i
[∂/∂X]と表すことができない場合があるが、それに関してはまた後で述べよう。
この考え方からすると、ボーア・ゾンマーフェルトの量子化条件∫p dq = nhは、以下のように考えることができる。p=−i [∂/∂q]であり、波動関数がei(位相)という形でかけていると思えば、pはすなわち、
[∂/∂q]であり、波動関数がei(位相)という形でかけていると思えば、pはすなわち、 [∂(位相)/∂q](−iとiが掛け算されて消えた)である。これにdqをかけて一周積分すれば、
[∂(位相)/∂q](−iとiが掛け算されて消えた)である。これにdqをかけて一周積分すれば、
| (7.13) |
| (7.14) |
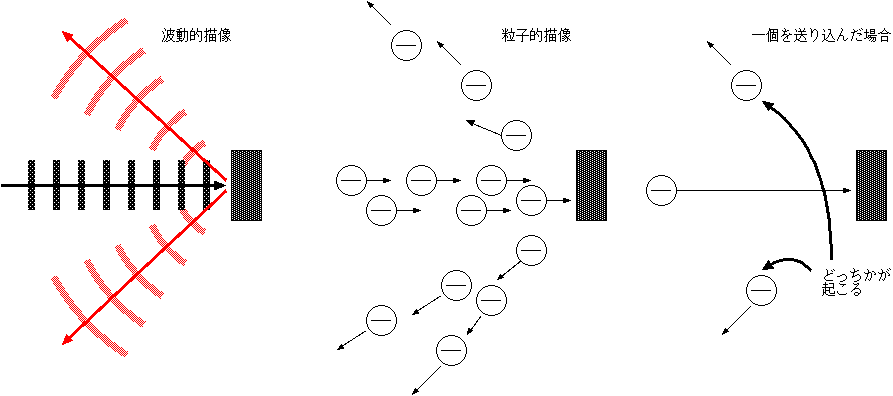
| 粒子的描像 | 波動的描像 |
| 光子(エネルギーhν) | 電場、磁場(→E,→H) |
| 物質粒子(エネルギー1/2mv2+V) | 波動関数(ψ) |
| (7.15) |
| (7.16) |
| (7.17) |
|
|
|
|
|
|
|
|